题目内容
11.用速度大小为v的中子轰击静止的锂核(${\;}_{3}^{6}$Li),发生核反应后生成氚核和α粒子.生成的氚核速度方向与中子的速度方向相反,氚核与α粒子的速率之比为7:8,质子和中子的质量均为m,光速为c:(1)写出核反应方程
(2)求氚核和α粒子的速度大小
(3)若核反应过程中放出的核能全部转化为α粒子和氚核的动能,求出质量亏损.
分析 (1)根据质量数守恒和电荷数守恒,书写核反应方程;
(2)中子轰击锂核的过程,系统的动量守恒,根据动量守恒定律以及氚核与α粒子的速率之比求解氦核和α粒子的速度;
(3)先求出核反应释放出的能量,再根据爱因斯坦质能方程求解质量亏损.
解答 解:(1)根据质量数守恒与电荷数守恒,则有核反应方程为:
${\;}_{0}^{1}$n+${\;}_{3}^{6}$Li→${\;}_{1}^{3}$H+${\;}_{2}^{4}$He;
(2)以中子的速度方向为正方向,由动量守恒定律得:
mnv=-mHv1+mHev2;
由题意得 v1:v2=7:8
解得:v1=$\frac{7v}{11}$,v2=$\frac{8v}{11}$
(3)氚核和α粒子的动能之和为:Ek=$\frac{1}{2}•3m{v}_{1}^{2}$+$\frac{1}{2}•4m{v}_{2}^{2}$=$\frac{403}{243}m{v}^{2}$
释放的核能为:△E=Ek-Ekn=$\frac{403}{243}m{v}^{2}$-$\frac{1}{2}m{v}^{2}$=$\frac{141}{121}m{v}^{2}$
由爱因斯坦质能方程得,质量亏损为:
△m=$\frac{△E}{{c}^{2}}$=$\frac{141m{v}^{2}}{121{c}^{2}}$
答:
(1)核反应方程为:${\;}_{0}^{1}$n+${\;}_{3}^{6}$Li→${\;}_{1}^{3}$H+${\;}_{2}^{4}$He;
(2)氚核和α粒子的速度大小分别为$\frac{7v}{11}$和$\frac{8v}{11}$.
(3)质量亏损为$\frac{141m{v}^{2}}{121{c}^{2}}$.
点评 核反应中遵守两大基本规律:能量守恒定律和动量守恒定律.注意动量守恒定律的矢量性,要明确是如何转化的.

 每课必练系列答案
每课必练系列答案 在粗糙水平面上,物块甲以v1=4m/s的速度向右匀速直线运动,物块乙的水平方向仅受摩擦力作用而向右做匀减速运动,加速度大小a=2m/s2.某时刻乙的速度为v2=10m/s,甲乙相距L=7m,如图所示.那么,从此时刻开始计时,物块甲追上物块乙需要的时间为
在粗糙水平面上,物块甲以v1=4m/s的速度向右匀速直线运动,物块乙的水平方向仅受摩擦力作用而向右做匀减速运动,加速度大小a=2m/s2.某时刻乙的速度为v2=10m/s,甲乙相距L=7m,如图所示.那么,从此时刻开始计时,物块甲追上物块乙需要的时间为( )
| A. | 10.0s | B. | 9.0s | C. | 8.0s | D. | 7.0s |
| A. | 1.8J,增加0.55J | B. | 1.8J,减小1.8J | C. | 0.55J,增加0.55J | D. | 0.55J,减小0.55J |
 把质量是0.2kg的小球放在竖立的弹簧上,并把小球往下按至A的位置,如图甲所示,迅速松手,弹簧把球弹起,球升至最高位置C(图丙所示),途中经过位置B时弹簧恰好处于自由状态(图乙所示).已知B、A高度差为0.1m,C、B的高度差为0.2m,弹簧的质量和空气的阻力均不计.则下列正确的是( )
把质量是0.2kg的小球放在竖立的弹簧上,并把小球往下按至A的位置,如图甲所示,迅速松手,弹簧把球弹起,球升至最高位置C(图丙所示),途中经过位置B时弹簧恰好处于自由状态(图乙所示).已知B、A高度差为0.1m,C、B的高度差为0.2m,弹簧的质量和空气的阻力均不计.则下列正确的是( )| A. | 在A位置,弹簧具有的弹性势能为0.6J | |
| B. | 在B位置小球动能最大 | |
| C. | 从A→C位置,小球机械能守恒 | |
| D. | 从A→C位置小球重力势能的增加量大于弹簧弹性势能的减少量 |

| A. | 小球A的机械能守恒 | |
| B. | 小球B的机械能增加 | |
| C. | 杆对A球做负功 | |
| D. | 两球在光滑水平面上运动的速度不变 |
 某同学研究电子在匀强电场中的运动时,电子仅受电场力作用,得到了电子由 a点运动到b点的轨迹(虚线所示),图中一组平行实线可能是电场线,也可能是等势面,则下列说法正确的是( )
某同学研究电子在匀强电场中的运动时,电子仅受电场力作用,得到了电子由 a点运动到b点的轨迹(虚线所示),图中一组平行实线可能是电场线,也可能是等势面,则下列说法正确的是( )| A. | 如果图中实线是电场线,电子在a点动能较小 | |
| B. | 如果图中实线是等势面,电子在a点电势能较小 | |
| C. | 不论图中实线是电场线还是等势面,a点的电势都比b点低 | |
| D. | 不论图中实线是电场线还是等势面,a点的加速度都比b点小 |
(1)打点计时器打点的时间间隔为0.1s,从打A点打到G点共历时0.6s.

(2)将B、C、D、E、F各个时刻的瞬时速度标在直角坐标系中,并在图乙中画出小车的瞬时速度随时间变化的关系图线.
| VB | VC | VD | VE | VF | |
| 数值(m/s) | 0.400 | 0.479 | 0.560 | 0.640 | 0.721 |
(4)此实验中,根据打点计时器打出的纸带,下列选项中:
A.时间间隔 B.位移 C.加速度 D.平均速度 E.瞬时速度
我们可以从纸带上直接得到的物理量是A,测量得到的物理量是B,通过计算得到的物理量是CDE.
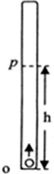 如图所示是一种测量重力加速度g的装置.在某星球上,将真空长直管沿竖直方向放置,管内小球以某一初速度自O点竖直上抛,经t时间上升到最高点,OP间的距离为h,已知引力常量为G,星球的半径为R.求:
如图所示是一种测量重力加速度g的装置.在某星球上,将真空长直管沿竖直方向放置,管内小球以某一初速度自O点竖直上抛,经t时间上升到最高点,OP间的距离为h,已知引力常量为G,星球的半径为R.求: