题目内容
15．
如图为一弹簧振子在AC间振动，图中黑点为振子球心的位置．（1）画出振子位于C点时离开平衡位置O的位移．
（2）标出振子位于A点时加速度的方向．
分析 位移是从平衡位置到末位置的有向线段；加速度与位移反向，指向平衡位置．
解答 解：（1）位移是从平衡位置到末位置的有向线段，如图；
（2）加速度与位移反向，总是指向平衡位置，如图所示：
答：如图所示．
点评 本题关键明确振幅、周期的概念，知道加速度与位移反向，总是指向平衡位置即可，会画实物图，基础题．
练习册系列答案
开心试卷期末冲刺100分系列答案
双基同步导航训练系列答案
相关题目
9．电荷+Q激发的电场中有A、B两点．质量为m，电量为q的带正电的粒子，自A点由静止释放，经过B点时的速度为v0；若此粒子的质量为2q，质量为4m，仍从A点由静止释放（粒子重力均不计），则经过B点时的速度变为（ ）
| A． | 2v0 | B． | 4v0 | C． | $\frac{{v}_{0}}{2}$ | D． | $\frac{v_0}{{\sqrt{2}}}$ |
3．
甲、乙两个完全相同的带电粒子，以相同的动能在匀强磁场中运动．甲从B1区运动到B2区，且B2＞B1，如图甲所示；乙在匀强磁场中做匀速圆周运动，且在△t时间内，磁感强度从B1增大到B2，如图乙所示；当磁感强度为B2时，甲、乙两粒子的动能变化为（ ）
甲、乙两个完全相同的带电粒子，以相同的动能在匀强磁场中运动．甲从B1区运动到B2区，且B2＞B1，如图甲所示；乙在匀强磁场中做匀速圆周运动，且在△t时间内，磁感强度从B1增大到B2，如图乙所示；当磁感强度为B2时，甲、乙两粒子的动能变化为（ ）| A． | 都不变 | B． | 甲不变，乙减少 | C． | 甲不变，乙增大 | D． | 甲减少，乙不变 |
10．
现有一质量均匀分布的直杆，绕通过垂直于直杆的水平转轴转动时形成一个摆，称为复摆，如图所示．复摆的周期可以表示为T=2π$\sqrt{\frac{I}{mgh}}$，其中m为直杆的质量，g为重力加速度，h为转轴到直杆质量中心的距离，I为直杆对转轴的转动惯量（描述物体绕转轴转动时的惯性）．当h=0时，I=ml2，其中l称为直杆绕通过质量中心且垂直于直杆的水平转轴转动时的回转半径．一般情况下，复摆对转轴的转动惯量可以表示为I=ml2+mh2，右表为实验中测量的一h组和复摆周期T的值，请用作图法求回转半径l和实验室当地的重力加速度g（要求保留小数点后两位有效数字）
现有一质量均匀分布的直杆，绕通过垂直于直杆的水平转轴转动时形成一个摆，称为复摆，如图所示．复摆的周期可以表示为T=2π$\sqrt{\frac{I}{mgh}}$，其中m为直杆的质量，g为重力加速度，h为转轴到直杆质量中心的距离，I为直杆对转轴的转动惯量（描述物体绕转轴转动时的惯性）．当h=0时，I=ml2，其中l称为直杆绕通过质量中心且垂直于直杆的水平转轴转动时的回转半径．一般情况下，复摆对转轴的转动惯量可以表示为I=ml2+mh2，右表为实验中测量的一h组和复摆周期T的值，请用作图法求回转半径l和实验室当地的重力加速度g（要求保留小数点后两位有效数字）| T（s） | 1.56 | 1.51 | 1.50 | 1.53 | 1.54 | 1.59 |
| h（m） | 0.20 | 0.25 | 0.30 | 0.35 | 0.40 | 0.45 |
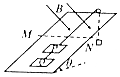如图所示，光滑固定斜面倾角为θ=37°，斜面上有两个完全相同的正方形线框P、Q用细线连接，P通过平行于斜面的细线绕过斜面顶端的定滑轮与一重物相连接，开始重物固定，线框处于静止，斜面上水平虚线MN上方有垂直于斜面向下的匀强磁场，磁感应强度大小为B，线框的边长及P线框最上边到MN的距离均为L，释放重物，使重物带动线框沿斜面向上运动，两个线框的质量均为m，每个线框的电阻均为R，重物的质量为2m，虚线上方的斜面足够长，重物离地面足够高，线框运动过程中，上边始终与MN平行，重力加速度为g，当线框P刚好要完全进入磁场的一瞬间，重物的加速度为零，sin37°=0.6，cos37°=0.8，求：
两个大轮半径相等的皮带轮的结构如图所示，A、B两点的半径之比为2：1，则A、B、C三点的角速度大小之比为ωA：ωB：ωC=2：2：1，这三点的向心加速度大小之比为aA：aB：aC=4：2：1．
4．
位于竖直平面内的光滑轨道由四分之一圆弧ab和抛物线bc组成，圆弧半径Oa水平，b点为抛物线顶点．已知h，s及重力加速度大小g，下列说法不正确的是（ ）
位于竖直平面内的光滑轨道由四分之一圆弧ab和抛物线bc组成，圆弧半径Oa水平，b点为抛物线顶点．已知h，s及重力加速度大小g，下列说法不正确的是（ ）| A． | 若将一小环从a释放且在bc段与环恰无作用力，则从其它任一点释放，环的加速度都小于g | |
| B． | 无论小环从a或从b释放，都可求出落地前速度的水平分量 | |
| C． | 若将一小环从a释放且在bc段与环恰无作用力，则可求出圆弧段的半径 | |
| D． | 无论小环从a或从b释放，都可求出落地前小环的运动时间 |
5．关于匀变速直线运动中加速度的正负，下列说法中正确的是（ ）
| A． | 匀加速直线运动中，加速度一定是正值 | |
| B． | 匀减速直线运动中，加速度一定是负值 | |
| C． | 只有在规定了初速度方向为正方向的前提下，匀加速直线运动加速度才取正值 | |
| D． | 以上说法都不对 |