题目内容
13. 如图所示,质量为m的光滑曲面,静止放在光滑的水平地面上,一质量也为m的小球以速度v冲向斜面,恰好能冲到曲面的顶端,然后再沿曲面滑落下来,当地的重力加速度为g.求:
如图所示,质量为m的光滑曲面,静止放在光滑的水平地面上,一质量也为m的小球以速度v冲向斜面,恰好能冲到曲面的顶端,然后再沿曲面滑落下来,当地的重力加速度为g.求:①曲面的高度h;
②曲面最终的速度.
分析 小球在曲面体上滑动的过程中,小球和曲面体组成的系统,水平方向不受外力,水平方向动量守恒,系统的机械能也守恒,根据两个守恒列方程求解小球从曲面体的高度,和曲面体的最终速度.
解答 解:(1)当小球冲到曲面顶端时,速度与曲面速度相同,竖直方向速度为零,以小球初速度v的方向为正,小球和曲面体组成的系统,由水平方向动量守恒和机械能守恒得:
mv=2mv1,$\frac{1}{2}m{v}^{2}=2×\frac{1}{2}m{{v}_{1}}^{2}+mgh$,
解得:h=$\frac{{v}^{2}}{4g}$
(2)设小球滑到地面上时的速度为v2,斜面的速度为v3,根据动量守恒定律得:
mv=mv2+mv3,
根据机械能守恒定律得:
$\frac{1}{2}m{v}^{2}=\frac{1}{2}m{{v}_{2}}^{2}+\frac{1}{2}m{{v}_{3}}^{2}$
解得:v2=0,v3=v
答:(1)曲面的高度为$\frac{{v}^{2}}{4g}$;
②曲面最终的速度为v.
点评 本题是系统动量守恒和机械能守恒的类型,类似于弹性碰撞,常见类型,知道恰好能冲到曲面的顶端,说明此时,小球竖直方向速度为零,难度不大,属于基础题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
19.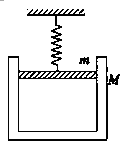 如图所示,活塞的质量为m.缸套的质量为M,通过弹簧吊在天花板上,气缸内封住一定质量的空气,缸套与活塞无摩擦,活塞截面积为S,大气压强为p0,则( )
如图所示,活塞的质量为m.缸套的质量为M,通过弹簧吊在天花板上,气缸内封住一定质量的空气,缸套与活塞无摩擦,活塞截面积为S,大气压强为p0,则( )
 如图所示,活塞的质量为m.缸套的质量为M,通过弹簧吊在天花板上,气缸内封住一定质量的空气,缸套与活塞无摩擦,活塞截面积为S,大气压强为p0,则( )
如图所示,活塞的质量为m.缸套的质量为M,通过弹簧吊在天花板上,气缸内封住一定质量的空气,缸套与活塞无摩擦,活塞截面积为S,大气压强为p0,则( )| A. | 汽缸内空气的压强等于p0-$\frac{Mg}{S}$ | B. | 汽缸内空气的压强等于p0+$\frac{mg}{S}$ | ||
| C. | 内外空气对缸套的作用力为(M+m)g | D. | 内外空气对活塞的作用力为Mg |
5.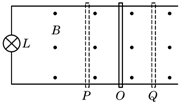 如图所示,接有灯泡L(阻值为R)的平行金属导轨(间距为l,电阻忽略不计)水平放置在磁感应强度为B的匀强磁场中.在外力F的作用下,一电阻可忽略的导体杆与两导轨良好接触并在P、Q两位置间做往复运动.从杆通过O位置,并沿OP方向运动时开始计时,其运动的速度-时间关系为v=v0cosωt,则下列说法中正确的是( )
如图所示,接有灯泡L(阻值为R)的平行金属导轨(间距为l,电阻忽略不计)水平放置在磁感应强度为B的匀强磁场中.在外力F的作用下,一电阻可忽略的导体杆与两导轨良好接触并在P、Q两位置间做往复运动.从杆通过O位置,并沿OP方向运动时开始计时,其运动的速度-时间关系为v=v0cosωt,则下列说法中正确的是( )
 如图所示,接有灯泡L(阻值为R)的平行金属导轨(间距为l,电阻忽略不计)水平放置在磁感应强度为B的匀强磁场中.在外力F的作用下,一电阻可忽略的导体杆与两导轨良好接触并在P、Q两位置间做往复运动.从杆通过O位置,并沿OP方向运动时开始计时,其运动的速度-时间关系为v=v0cosωt,则下列说法中正确的是( )
如图所示,接有灯泡L(阻值为R)的平行金属导轨(间距为l,电阻忽略不计)水平放置在磁感应强度为B的匀强磁场中.在外力F的作用下,一电阻可忽略的导体杆与两导轨良好接触并在P、Q两位置间做往复运动.从杆通过O位置,并沿OP方向运动时开始计时,其运动的速度-时间关系为v=v0cosωt,则下列说法中正确的是( )| A. | 杆中电流与时间的关系为i=$\frac{Bl{v}_{0}cosωt}{R}$ | |
| B. | 杆所受安培力与时间的关系为FA=$\frac{{B}^{2}{l}^{2}{v}_{0}sinωt}{R}$ | |
| C. | 杆克服安培力做功的功率与时间的关系为p=$\frac{(Bl{v}_{0}cosωt)^{2}}{R}$ | |
| D. | 杆运动一个周期,回路中产生的焦耳热为Q=$\frac{{B}^{2}{l}^{2}{{v}_{0}}^{2}π}{Rω}$ |
2.一电场的电场线分布如图所示,电场中有A、B、C三点,且AB=BC,则下列关系中正确的是( )


| A. | 电场强度大小关系为EA=EC>EB | |
| B. | 电势φA=φC>φB | |
| C. | 将一带负电粒子由A经B移至C点过程中,电场力先做负功再做正功 | |
| D. | 将一带正电粒子由A经B移至C点过程中,电势能先增大再减小 |
3.如图甲所示,一绝缘的竖直圆环上均匀分布着正电荷,一光滑细杆从圆心垂直圆环平面穿过圆环,杆上套有带正电的小球,现使小球从a点由静止释放,并开始计时,后经过b、c两点,其运动过程中的υ-t图象如图乙所示.下列说法正确的是( )


| A. | 带电圆环在圆心处产生的场强为零 | |
| B. | a点场强大于b点场强 | |
| C. | 电势差Uab小于Ubc | |
| D. | 小球由b到c的过程中平均速度小于0.55m/s |
 如图,一木块通过长度忽略不计的绳固定在小车的前壁上,小车上表面光滑.某时刻小车由静止开始向右匀加速运动,经过2s,细绳断裂.细绳断裂后,小车的加速度不变,又经过一段时间,滑块从小车左端刚好掉下,在这段时间内,已知滑块相对小车前3s内滑行了4.5m;后3s内滑行了10.5m.
如图,一木块通过长度忽略不计的绳固定在小车的前壁上,小车上表面光滑.某时刻小车由静止开始向右匀加速运动,经过2s,细绳断裂.细绳断裂后,小车的加速度不变,又经过一段时间,滑块从小车左端刚好掉下,在这段时间内,已知滑块相对小车前3s内滑行了4.5m;后3s内滑行了10.5m.
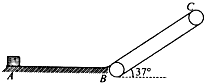 如图所示为仓库中常用的皮带传输装置示意图.传送带BC与水平平台AB的夹角θ=37°,其交接处由很小的圆弧平滑连接,平台左端A处一质量为m=30kg的货物,在F=350N水平推力的作用下由静止开始向传送带运动,经时间t1=1.5s到达平台AB的中点,此时撤去外力F,货物继续向前运动,不计货物经过B处的机械能损失.已知货物与平台和传送带间的动摩擦因数均为0.5,B、C两端相距4.45m,g=10m/s2,cos37°=0.8,sin37°=0.6.求:
如图所示为仓库中常用的皮带传输装置示意图.传送带BC与水平平台AB的夹角θ=37°,其交接处由很小的圆弧平滑连接,平台左端A处一质量为m=30kg的货物,在F=350N水平推力的作用下由静止开始向传送带运动,经时间t1=1.5s到达平台AB的中点,此时撤去外力F,货物继续向前运动,不计货物经过B处的机械能损失.已知货物与平台和传送带间的动摩擦因数均为0.5,B、C两端相距4.45m,g=10m/s2,cos37°=0.8,sin37°=0.6.求: 如图所示,两根完全相同的光滑金属导轨OP、OQ固定在水平桌面上,导轨间的夹角为θ=74°.导轨所在空间有垂直于桌面向下的匀强磁场,磁感应强度大小为B1=0.2T.t=0时刻,一长为L=1m的金属杆MN在外力作用下以恒定速度v=0.2m/s从O点开始向右滑动.在滑动过程中金属杆MN与导轨接触良好,且始终垂直于两导轨夹角的平分线,金属杆的中点始终在两导轨夹角的平分线上.导轨与金属杆单位长度的电阻均为r0=0.1Ω.求
如图所示,两根完全相同的光滑金属导轨OP、OQ固定在水平桌面上,导轨间的夹角为θ=74°.导轨所在空间有垂直于桌面向下的匀强磁场,磁感应强度大小为B1=0.2T.t=0时刻,一长为L=1m的金属杆MN在外力作用下以恒定速度v=0.2m/s从O点开始向右滑动.在滑动过程中金属杆MN与导轨接触良好,且始终垂直于两导轨夹角的平分线,金属杆的中点始终在两导轨夹角的平分线上.导轨与金属杆单位长度的电阻均为r0=0.1Ω.求