��Ŀ����
1����ͼΪ����֤��ײ�ж����غ㡱��ʵ��װ��
������˵���в����ϱ�ʵ��Ҫ�����D��
A��������Ȱ����������ߵ�ֱ��������ͬ
B����ͬһ��ʵ��IJ�ͬ��ײ�У�ÿ������������ͬһ�߶��ɾ�ֹ�ͷ�
C����װ���ʱ�����ĩ�˱���ˮƽ
D����Ҫʹ�õIJ�����������ƽ�Ϳ̶ȳߺ�������������С��ӹ��ĩ�˵����ڼ�¼ֽ�ϵ�ʱ�䣮
��ʵ���м�¼�˹��ĩ���ڼ�¼ֽ�ϵ���ֱͶӰΪO�㣬������ͷ��������ڼ�¼ֽ���ҵ�������ƽ�����λ��ΪM��P��N����������ǵ�O��ľ���ֱ�Ϊ$\overline{OM}$��$\overline{OP}$��$\overline{ON}$����֪�����������Ϊm1�����������Ϊm2��������m1$\overline{OM}$+m2•$\overline{ON}$���Ƶ���m1$\overline{OP}$������Ϊ�ɹ���֤����ײ�еĶ����غ㣮
����ʵ���У���$\overline{OM}$��$\overline{OP}$��$\overline{ON}$����m2$\overline{ON}$2=m1$\overline{OP}$2-m1$\overline{OM}$2ʱ�����֤����ײ��ϵͳ�Ļ�е���غ㣨Ҫ���â��е���������ʾ����
���� ��Ҫʹ��������������������뾶Ӧ��ȣ�Ϊ��ֹ��������ײ���������������Ӧ���ڱ����������������ʵ��ԭ����ʵ��ע������������⣻
��Ӧ�ö����غ㶨�ɸ���ͼʾ�����Ҫ��֤�ı���ʽ��Ȼ��������⣮
��Ӧ�û�е���غ㶨�ɷ������⣮
��� �⣺��A��Ҫʹ��������������������뾶Ӧ��ȣ�Ϊ��ֹ��������ײ���������������Ӧ���ڰ��������������������Ȱ��������������������뾶Ӧ��ȣ���A��ȷ��
B��Ϊ����������ij��ٶ���ȣ���ͬһ��ʵ��IJ�ͬ��ײ�У�ÿ������������ͬһ�߶��ɾ�ֹ�ͷţ���B��ȷ��
C��Ϊ��֤С���뿪�������ƽ���˶���С���뿪���ʱ���ٶȱ���ˮƽ����װ���ʱ�����ĩ�˱���ˮƽ����C��ȷ��
D��С���뿪�������ƽ���˶���С���׳���ĸ߶���ͬ�������ڿ��е��˶�ʱ����ȣ�С���ˮƽλ������ٶȳ����ȣ�������С���ˮƽλ�ƴ���С��ij��ٶȣ�ʵ�鲻��Ҫ���С����˶�ʱ�䣬ʵ������Ҫ���С��������С���ˮƽλ�ƣ���Ҫʹ�õIJ�����������ƽ�Ϳ̶ȳߣ���D����
����ѡ����ģ���ѡD��
��������ײ����ƽ���˶��������׳���ĸ߶���ȣ��ڿ��е��˶�ʱ��t��ȣ���ײ���̶����غ㣬��m1v1=m1v1��+m2v2�䣬
����ͬʱ����ʱ��t�ã�m1v1t=m1v1��t+m2v2��t����m1$\overline{OP}$=m1$\overline{OM}$+m2$\overline{ON}$�����m1$\overline{OP}$=m1$\overline{OM}$+m2$\overline{ON}$������ײ�����У�ϵͳ�����غ㣮
�������ײ���̶����غ㣬��$\frac{1}{2}$m1v12=$\frac{1}{2}$m1v1��2+$\frac{1}{2}$m2v2��2��$\frac{1}{2}$m1��$\overline{OP}$��2=$\frac{1}{2}$m1��$\overline{OM}$��2+$\frac{1}{2}$m2��$\overline{ON}$��2��$\frac{1}{2}$m1$\overline{OP}$2=$\frac{1}{2}$m1$\overline{OM}$2+$\frac{1}{2}$m2$\overline{ON}$2��
�������m1$\overline{OP}$2=m1$\overline{OM}$2+m2$\overline{ON}$2��m2$\overline{ON}$2=m1$\overline{OP}$2-m1$\overline{OM}$2������ײ���̻�е���غ㣮
�ʴ�Ϊ����D����m1$\overline{OP}$����m2$\overline{ON}$2=m1$\overline{OP}$2-m1$\overline{OM}$2��
���� ���⿼����ʵ��ע�����ʵ�����ĵ�ѡ�����ݴ�����֪��ʵ��ԭ����ʵ��ע���������ȷ���⣻С���뿪�������ƽ���˶��������ڿ��е��˶�ʱ����ȣ�ˮƽλ������ٶ������ȣ�������ˮƽλ�Ʊ�ʾ���ٶȣ�

 ��ͼ��ʾ���̶��Ĵֲ���ֱ��������С���a�������쳤������ϸ��ͨ����С�ɺ��ԵĶ������������a��С���b������cdˮƽ�����ɾ�ֹ�ͷ�����飬���a��ͼʾλ����������ǡ���ܵ���c�����ڴ˹����У����������Ͷ�����֮���Ħ���Ϳ�������������˵����ȷ���ǣ�������
��ͼ��ʾ���̶��Ĵֲ���ֱ��������С���a�������쳤������ϸ��ͨ����С�ɺ��ԵĶ������������a��С���b������cdˮƽ�����ɾ�ֹ�ͷ�����飬���a��ͼʾλ����������ǡ���ܵ���c�����ڴ˹����У����������Ͷ�����֮���Ħ���Ϳ�������������˵����ȷ���ǣ�������| A�� | ���a����c��ʱ���ٶ�Ϊ�� | |
| B�� | �����������a���Ĺ��������a�������ܵ������� | |
| C�� | �����������aʼ�������� | |
| D�� | Ħ������a���Ĺ��������a��bϵͳ��е�ܵı仯�� |
 ��ͼ��ʾ��һ�뾶ΪR�Ĺ⻬Բ�������ˮƽ�����У�һС����Բ������ĵ����Ϊx���ָ�С��һ���ٶȣ���ǡ��ͨ��Բ�������ߵ㣬��֪С����ˮƽ��Ķ�Ħ������Ϊ�̣���С����ٶȵĴ�С��
��ͼ��ʾ��һ�뾶ΪR�Ĺ⻬Բ�������ˮƽ�����У�һС����Բ������ĵ����Ϊx���ָ�С��һ���ٶȣ���ǡ��ͨ��Բ�������ߵ㣬��֪С����ˮƽ��Ķ�Ħ������Ϊ�̣���С����ٶȵĴ�С��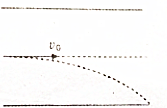 �������ơ���ӡ����ƫת�糡��ͼ��ʾ���������ĵ���ΪC���峤ΪL����������Ϊd������һ��������Ϊq������Ϊm��ī�������Գ��ٶ�v0������������ߴ�ֱ�糡����ƫת�糡�У���ī����ǡ�ܴӼ����Ե����糡����������������
�������ơ���ӡ����ƫת�糡��ͼ��ʾ���������ĵ���ΪC���峤ΪL����������Ϊd������һ��������Ϊq������Ϊm��ī�������Գ��ٶ�v0������������ߴ�ֱ�糡����ƫת�糡�У���ī����ǡ�ܴӼ����Ե����糡���������������� ��ͼ��ʾ������Ϊm�Ĺ⻬���棬��ֹ���ڹ⻬��ˮƽ�����ϣ�һ����ҲΪm��С�����ٶ�v����б�棬ǡ���ܳ嵽����Ķ��ˣ�Ȼ���������滬�����������ص��������ٶ�Ϊg����
��ͼ��ʾ������Ϊm�Ĺ⻬���棬��ֹ���ڹ⻬��ˮƽ�����ϣ�һ����ҲΪm��С�����ٶ�v����б�棬ǡ���ܳ嵽����Ķ��ˣ�Ȼ���������滬�����������ص��������ٶ�Ϊg����
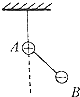
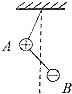
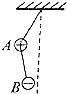
 ��ͼ��ʾ��A��B������С��������ֲ�Ϊ2m��m�����������ֲ�Ϊ3q��-q��������þ�Եϸ��������A�����õȳ��ľ�Եϸ���������컨���ϣ�����Ĵ�С�ɺ��Բ��ƣ������������ڿռ���ˮƽ�������ǿ�糡���糡ǿ��ΪE��ƽ��ʱϸ�߶���������ƽ��ʱ�Ŀ���λ����ͼ�еģ�������
��ͼ��ʾ��A��B������С��������ֲ�Ϊ2m��m�����������ֲ�Ϊ3q��-q��������þ�Եϸ��������A�����õȳ��ľ�Եϸ���������컨���ϣ�����Ĵ�С�ɺ��Բ��ƣ������������ڿռ���ˮƽ�������ǿ�糡���糡ǿ��ΪE��ƽ��ʱϸ�߶���������ƽ��ʱ�Ŀ���λ����ͼ�еģ�������