题目内容
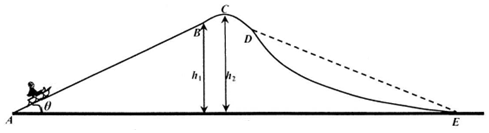
12.雪橇运动在北方很受人们欢迎,其简化模型如图所示.倾角θ=37°的直线雪道AB与曲线雪道BCDE在B点平滑连接,其中A、E两点在同一水平面上,雪道最高点C所对应的圆弧半径R=10m,B、C两点距离水平面AE的高度分别为h1=18m、h2=18.1m,雪橇与雪道间的动摩擦因数μ=0.1.游客可坐在电动雪橇上由A点从静止开始向上运动.若电动雪橇以恒定功率P=1.03kW工作t=10s时间后自动关闭,则雪橇和游客(总质量M=50kg)到达C点时的速度vC=1m/s,到达E点时的速度vE=9m/s.已知雪橇运动过程中不脱离雪道,sin37°=0.6,重力加速度g取10m/s2.(1)求雪橇在C点时对雪道的压力;
(2)求雪橇在BC段克服摩擦力做的功;
(3)求雪橇和游客的整体从C点运动到E点过程中损失的机械能;
(4)若仅将DE段改成与曲线雪道CD段平滑连接的倾斜直线轨道(如图中虚线所示),则雪橇和游客的整体从C点运动到E点过程中损失的机械能将增加还是减少?请简要说明理由.
分析 (1)选雪橇和游客的整体为研究对象,对其运动到C点进行受力分析,运用牛顿第二定律即可求出雪橇在C点时对雪道的压力;
(2)从A到C对雪橇和游客的整体运用动能定理,即可求出雪橇在BC段克服摩擦力做的功;
(3)对整体从C到E运用动能定理,求出摩擦力做功,根据功能原理即可求出C点运动到E点过程中损失的机械能;
(4)运用微积分思想求出曲线轨道上摩擦力做功,与倾斜直线轨道上摩擦力做功做比较,即可判断雪橇和游客的整体从C点运动到E点过程中损失机械能的情况.
解答 解:(1)设C点轨道对雪橇的支持力为NC,根据牛顿第二定律可得:NC-Mg=M$\frac{{v}_{C}^{2}}{R}$
解得:NC=Mg+M$\frac{{v}_{C}^{2}}{R}$=50×10+50×$\frac{{1}^{2}}{10}$N=505N
根据牛顿第三定律可得,雪橇在C点时对雪道的压力:NC′=NC=505N
(2)设雪橇在BC段克服摩擦力做的功为WBC,
从A到C对雪橇和游客的整体运用动能定理可得:Pt-Mgh2-μMg•$\frac{{h}_{1}}{sinθ}$•cosθ-WBC=$\frac{1}{2}M{v}_{C}^{2}$
解得:WBC=25J
(3)对整体从C到E运用动能定理可得:Mgh2-WCE=$\frac{1}{2}M{v}_{E}^{2}$-$\frac{1}{2}M{v}_{C}^{2}$
从C到E克服摩擦力做功:WCE=7050J
所以整体从C点运动到E点过程中损失的机械能:W损=WCE=7050J
(4)设D到E的水平距离为L,
平滑连接的倾斜直线轨道倾角为θ,摩擦力做功:Wf1=-μmgcosθ•$\frac{L}{cosθ}$=μmgL
曲线轨道上任选极短一段如图所示,将这一小段近似看成倾角为α的倾斜直线轨道,该端轨道在水平方向上的投影长为△x,
则摩擦力在该段轨道上做功:Wf=-μmgcosα•△x$\frac{1}{cosα}$=μmg△x
所以整个曲线轨道摩擦力做功等于每一小段摩擦力做功的累加,即:Wf2=-μmg∑△x=μmgL
故两轨道的摩擦力做功相同:Wf1=Wf2=△E损
所以雪橇和游客的整体从C点运动到E点过程中损失的机械能相同.
答:(1)雪橇在C点时对雪道的压力为505N;
(2)雪橇在BC段克服摩擦力做的功为25J;
(3)雪橇和人的整体从C点运动到E点过程中损失的机械能为7050J;
(4)若仅将DE段改成与曲线雪道CD段平滑连接的倾斜直线轨道,则雪橇从C点运动到E点过程中损失的机械能不变,证明过程见解析.
点评 本题考查动能定理的综合运用,解题关键是要分好过程,明确每一个过程的运动形式,选择合适的规律解决问题,注意运用W=Pt去求解功率恒定的变力做功;注意理解体会第(3)问中运用的微积分思想.

| A. | 气体自发地扩散运动总是向着更为无序的方向进行,是可逆过程 | |
| B. | 第二类永动机虽然不违反能量守恒定律,所以是能制造出来的 | |
| C. | 第一类永动机的思想违背了能量守恒定律,所以是不可能制成的 | |
| D. | 一定质量的理想气体向真空自由膨胀时,体积增大,熵减小 |
 如图所示,两根足够长的光滑导轨固定竖直放置,间距为L,底端接阻值为R的电阻.将质量为m的金属棒悬挂在一固定的轻弹簧下端,金属棒和导轨接触良好,导轨所在平面与磁感应强度为B的匀强磁场垂直,金属棒和导轨电阻不计,现将金属棒从弹簧原长位置由静止释放(设当地重力加速度为g),则( )
如图所示,两根足够长的光滑导轨固定竖直放置,间距为L,底端接阻值为R的电阻.将质量为m的金属棒悬挂在一固定的轻弹簧下端,金属棒和导轨接触良好,导轨所在平面与磁感应强度为B的匀强磁场垂直,金属棒和导轨电阻不计,现将金属棒从弹簧原长位置由静止释放(设当地重力加速度为g),则( )| A. | 释放瞬间金属棒的加速度小于重力加速度g | |
| B. | 金属棒向下的最大速度为v时,所受弹簧弹力为F=mg-$\frac{{B}^{2}{L}^{2}v}{R}$ | |
| C. | 金属棒向下运动时,流过电阻R的电流方向为a→b | |
| D. | 电路中产生的总热量等于金属棒重力势能的减少量 |
 北京时间2013年10月29日10时50分,中国在太原卫星发射中心用“长征二号丙”运载火箭,成功将遥感卫星十八号发射升空,卫星顺利进人预定轨道.图是火箭点火升空瞬间的照片.对这一瞬间火箭的速度和加速度的判断正确的是( )
北京时间2013年10月29日10时50分,中国在太原卫星发射中心用“长征二号丙”运载火箭,成功将遥感卫星十八号发射升空,卫星顺利进人预定轨道.图是火箭点火升空瞬间的照片.对这一瞬间火箭的速度和加速度的判断正确的是( )| A. | 火箭的速度很小,加速度不为0 | B. | 火箭的速度很小,加速度为0 | ||
| C. | 火箭的速度很大,加速度很大 | D. | 火箭的速度很大,加速度很小 |
 如图所示,半径R=0.2m的$\frac{1}{4}$光滑圆弧轨道AB与粗糙的水平轨道BC相切与M点.质量m=2kg(可视为质点)从最高点A由静止滑下,最后停在BC上.取g=10m/s2,求:
如图所示,半径R=0.2m的$\frac{1}{4}$光滑圆弧轨道AB与粗糙的水平轨道BC相切与M点.质量m=2kg(可视为质点)从最高点A由静止滑下,最后停在BC上.取g=10m/s2,求: 如图所示,与质量为m=2kg的小物块初速为零的轻放在水平匀速运动的传送带上的A点,随传送带运动到B点,小物块从C点沿圆弧切线进入竖直的半圆轨道恰能做圆周运动,已知圆弧半径R=1.5m,轨道最低点为D,D点距水平面的高度h=5m.小物块离开D点后(只有D点下区域有风),由于受到恒定的水平风力的作用,球竖直地落入距击球点水平距离为L=3.75m的E点.已知小物块与传送带间的动摩擦因数μ=0.3,传送带以5m/s恒定速率顺时针转动,g=10m/s2.求:
如图所示,与质量为m=2kg的小物块初速为零的轻放在水平匀速运动的传送带上的A点,随传送带运动到B点,小物块从C点沿圆弧切线进入竖直的半圆轨道恰能做圆周运动,已知圆弧半径R=1.5m,轨道最低点为D,D点距水平面的高度h=5m.小物块离开D点后(只有D点下区域有风),由于受到恒定的水平风力的作用,球竖直地落入距击球点水平距离为L=3.75m的E点.已知小物块与传送带间的动摩擦因数μ=0.3,传送带以5m/s恒定速率顺时针转动,g=10m/s2.求: 如图,汽车质量为1.5×104kg,以不变的速率5$\sqrt{2}$m/s先后驶过凹形路面和凸形路面,路面圆弧半径均为15m.求:
如图,汽车质量为1.5×104kg,以不变的速率5$\sqrt{2}$m/s先后驶过凹形路面和凸形路面,路面圆弧半径均为15m.求: 在用如图所示的装置做验证机械能守恒的实验中,若实验操作正确,则实验打出的纸带可能是下列选项中的 ( )
在用如图所示的装置做验证机械能守恒的实验中,若实验操作正确,则实验打出的纸带可能是下列选项中的 ( )


