题目内容
20. 如图,汽车质量为1.5×104kg,以不变的速率5$\sqrt{2}$m/s先后驶过凹形路面和凸形路面,路面圆弧半径均为15m.求:
如图,汽车质量为1.5×104kg,以不变的速率5$\sqrt{2}$m/s先后驶过凹形路面和凸形路面,路面圆弧半径均为15m.求:(1)汽车以此速率驶过凹形路面压力是多少?
(2)汽车以此速率驶过凸形路面压力是多少?(g取10m/s2)
分析 在凹形路面的最低点和凸形路面的最高点,汽车靠重力和支持力的合力提供向心力,结合牛顿第二定律求出支持力的大小,从而得出压力的大小.
解答 解:(1)在凹形路面的最低点,根据牛顿第二定律得,N-mg=m$\frac{{v}^{2}}{R}$,
解得支持力N=$mg+m\frac{{v}^{2}}{R}=1.5×1{0}^{5}+1.5×1{0}^{4}×\frac{50}{15}$N=2×105N.
根据牛顿第三定律知,汽车以此速率驶过凹形路面的压力为2×105N.
(2)在凸形路面的最高点,根据牛顿第二定律得,$mg-N′=m\frac{{v}^{2}}{R}$,
解得支持力$N′=mg-m\frac{{v}^{2}}{R}$=$1.5×1{0}^{5}-1.5×1{0}^{4}×\frac{50}{15}$N=1.0×105N.
根据牛顿第三定律知,汽车以此速率驶过凹形路面的压力为1.0×105N.
答:(1)汽车以此速率驶过凹形路面压力是2×105N.
(2)汽车以此速率驶过凸形路面压力是1.0×105N.
点评 解决本题的关键知道最高点和最低点向心力的来源,结合牛顿第二定律进行求解,基础题.

练习册系列答案
相关题目
2.下列过程中利用了离心现象的是( )
| A. | 汽车减速过弯道 | B. | 足球运动员将足球踢出 | ||
| C. | 用力抖落衣服上的灰尘 | D. | 运动员旋转时抛出链球 |
5. 有两个边长不等的正方形ABCD和abcd,如图所示,且Aa、Bb、Cc、Dd的间距相等,在AB、AC、BD、CD边中点分别放等量的点电荷,其中AB、AC边中点放的点电荷带正电,CD、BD边中点放的点电荷带负电.取无穷远处电势为零,则下列说法正确的是( )
有两个边长不等的正方形ABCD和abcd,如图所示,且Aa、Bb、Cc、Dd的间距相等,在AB、AC、BD、CD边中点分别放等量的点电荷,其中AB、AC边中点放的点电荷带正电,CD、BD边中点放的点电荷带负电.取无穷远处电势为零,则下列说法正确的是( )
 有两个边长不等的正方形ABCD和abcd,如图所示,且Aa、Bb、Cc、Dd的间距相等,在AB、AC、BD、CD边中点分别放等量的点电荷,其中AB、AC边中点放的点电荷带正电,CD、BD边中点放的点电荷带负电.取无穷远处电势为零,则下列说法正确的是( )
有两个边长不等的正方形ABCD和abcd,如图所示,且Aa、Bb、Cc、Dd的间距相等,在AB、AC、BD、CD边中点分别放等量的点电荷,其中AB、AC边中点放的点电荷带正电,CD、BD边中点放的点电荷带负电.取无穷远处电势为零,则下列说法正确的是( )| A. | O点的电场强度和电势均为零 | |
| B. | 同一点电荷在a、d两点所受电场力相同 | |
| C. | 将一负点电荷由a点移到b点电势能将减小 | |
| D. | 把一正点电荷沿着b→d→c路径移动时,电场力做的功为负 |
9.两位同学分别在塔的同一高处,用两个轻重不同的小铁球做自由落体实验,已知甲球重力是乙球的两倍,则下落的过程中( )
| A. | 甲球的加速度是乙球的2倍 | B. | 甲、乙两球的加速度相间 | ||
| C. | 甲球先落地 | D. | 乙球先落地 |
 一辆平板车静止在水平地面上,质量M=2500kg.车上放一质量m=500kg的重物,重物前侧面到车前的距离为L=3m,如图所示.开始车以a=2m/s2的加速度匀加速启动,6s后改为匀速运动,有经过2s司机发现前方有障碍,立即制动刹车做匀减速运动直到静止,最终重物恰好滑动到车前壁处静止.已知平板车在加速和匀速运动过程中所受阻力大小为Ff=1000N,重物与平板间的动摩擦因数μ=0.4,认为重物与车平板间的最大静摩擦力等于滑动摩擦力,(g=10m/s2).求:
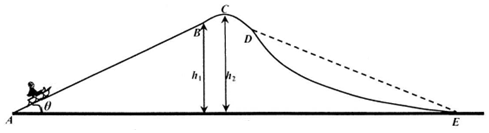
一辆平板车静止在水平地面上,质量M=2500kg.车上放一质量m=500kg的重物,重物前侧面到车前的距离为L=3m,如图所示.开始车以a=2m/s2的加速度匀加速启动,6s后改为匀速运动,有经过2s司机发现前方有障碍,立即制动刹车做匀减速运动直到静止,最终重物恰好滑动到车前壁处静止.已知平板车在加速和匀速运动过程中所受阻力大小为Ff=1000N,重物与平板间的动摩擦因数μ=0.4,认为重物与车平板间的最大静摩擦力等于滑动摩擦力,(g=10m/s2).求: 一轻弹簧下端栓接在倾角为θ的固定斜面底端,弹簧处于原长时上端位于斜面上的B点,B点以上光滑,B点到斜面底端粗糙,可视为质点的物体质量为m,以初速度v0从A点沿斜面向下运动,物体将弹簧压缩到最短后恰能被弹回到B点.AB间距离为L,物体与B点以下斜面的动摩擦因数为μ,已知重力加速度为g,不计空气阻力,求此过程中:
一轻弹簧下端栓接在倾角为θ的固定斜面底端,弹簧处于原长时上端位于斜面上的B点,B点以上光滑,B点到斜面底端粗糙,可视为质点的物体质量为m,以初速度v0从A点沿斜面向下运动,物体将弹簧压缩到最短后恰能被弹回到B点.AB间距离为L,物体与B点以下斜面的动摩擦因数为μ,已知重力加速度为g,不计空气阻力,求此过程中: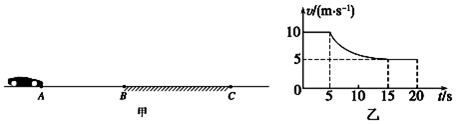
 如图所示,一个质量为10kg的物体放在光滑水平地面上,用50N的水平拉力F使物体由静止开始做匀加速直线运动.求:
如图所示,一个质量为10kg的物体放在光滑水平地面上,用50N的水平拉力F使物体由静止开始做匀加速直线运动.求: