题目内容
17.一宇宙飞船沿半径为2R(R为地球的半径)的圆轨道在地球赤道的正上方运行,其运行方向与地球自转同向,已知地球自转角速度为ω和地球表面的重力加速度g.(1)求出宇宙飞船的运行周期T;
(2)若某时刻,赤道上有一天文爱好者正好看到飞船在其正上方,问从此刻起天文爱好者能连续多长时间看到飞船.
分析 (1)宇宙飞船绕地球做匀速圆周运动,由地球的万有引力提供向心力,根据牛顿运动定律求解宇宙飞船的运行周期.
(2)宇宙飞船绕地球做匀速圆周运动,人随地球自转做匀速圆周运动,当宇宙飞船转过的角度与人转过的角度之差在$\frac{π}{2}$内时,天文爱好者可以连续观察到飞船.
解答 解:(1)宇宙飞船绕地球做圆周运动,万有引力提供向心力,由牛顿运动定律得:
G$\frac{Mm}{(2R)^{2}}$=m$(\frac{2π}{T})^{2}$•2R,
在地球表面的物体:G$\frac{Mm′}{{R}^{2}}$=m′g,
解得:T=4π$\sqrt{\frac{2R}{g}}$;
(2)以地面为参照物,宇宙飞船再次出现在天文爱好者上方时,当宇宙飞船转过的角度与人转过的角度之差在$\frac{π}{2}$内时,天文爱好者可以连续观察到飞船,即:
ω1△t-ω△t=$\frac{π}{2}$,
解得:△t=$\frac{π}{\sqrt{\frac{g}{2R}}-2ω}$
答:(1)出宇宙飞船的运行周期T为4π$\sqrt{\frac{2R}{g}}$;
(2)从此刻起天文爱好者能连续看到飞船的时间是:$\frac{π}{\sqrt{\frac{g}{2R}}-2ω}$.
点评 本题考查了求飞船的周期、天文爱好者观察到飞船的时间,考查了万有引力定律的应用,应用万有引力公式与牛顿第二定律可以解题,解题时注意“黄金代换”的应用.

练习册系列答案
相关题目
8.如图是某区域的电场线分布,A、B、C是电场中的三个点. 下列说法正确的是( )


| A. | A点的电场强度最强 | |
| B. | B点的电场强度最弱 | |
| C. | A、B、C三点的电场强度方向相同 | |
| D. | 正电荷、负电荷在B点受到的电场力方向相反 |
5. 如图所示为“割绳子”游戏中的一幅截图,游戏中割断左侧绳子糖果就会通过正下方第一颗星星,糖果一定能经过星星处吗?现将其中的物理问题抽象出来进行研究:三根不可伸长的轻绳共同系住一颗质量为m的糖果(可视为质点),设从左到右三根轻绳的长度分别为l1、l2和l3,其中最左侧的绳子处于竖直且张紧的状态,另两根绳均处于松弛状态,三根绳的上端分别固定在同一水平线上,且相邻两悬点间距离均为d,糖果正下方的第一颗星星与糖果距离为h.已知绳子由松弛到张紧时沿绳方向的速度分量即刻减为零,现将最左侧的绳子割断,以下选项正确的是( )
如图所示为“割绳子”游戏中的一幅截图,游戏中割断左侧绳子糖果就会通过正下方第一颗星星,糖果一定能经过星星处吗?现将其中的物理问题抽象出来进行研究:三根不可伸长的轻绳共同系住一颗质量为m的糖果(可视为质点),设从左到右三根轻绳的长度分别为l1、l2和l3,其中最左侧的绳子处于竖直且张紧的状态,另两根绳均处于松弛状态,三根绳的上端分别固定在同一水平线上,且相邻两悬点间距离均为d,糖果正下方的第一颗星星与糖果距离为h.已知绳子由松弛到张紧时沿绳方向的速度分量即刻减为零,现将最左侧的绳子割断,以下选项正确的是( )
 如图所示为“割绳子”游戏中的一幅截图,游戏中割断左侧绳子糖果就会通过正下方第一颗星星,糖果一定能经过星星处吗?现将其中的物理问题抽象出来进行研究:三根不可伸长的轻绳共同系住一颗质量为m的糖果(可视为质点),设从左到右三根轻绳的长度分别为l1、l2和l3,其中最左侧的绳子处于竖直且张紧的状态,另两根绳均处于松弛状态,三根绳的上端分别固定在同一水平线上,且相邻两悬点间距离均为d,糖果正下方的第一颗星星与糖果距离为h.已知绳子由松弛到张紧时沿绳方向的速度分量即刻减为零,现将最左侧的绳子割断,以下选项正确的是( )
如图所示为“割绳子”游戏中的一幅截图,游戏中割断左侧绳子糖果就会通过正下方第一颗星星,糖果一定能经过星星处吗?现将其中的物理问题抽象出来进行研究:三根不可伸长的轻绳共同系住一颗质量为m的糖果(可视为质点),设从左到右三根轻绳的长度分别为l1、l2和l3,其中最左侧的绳子处于竖直且张紧的状态,另两根绳均处于松弛状态,三根绳的上端分别固定在同一水平线上,且相邻两悬点间距离均为d,糖果正下方的第一颗星星与糖果距离为h.已知绳子由松弛到张紧时沿绳方向的速度分量即刻减为零,现将最左侧的绳子割断,以下选项正确的是( )| A. | 只要满足l2≥$\sqrt{({l}_{1}+h)^{2}+{d}^{2}}$,糖果就能经过正下方第一颗星星处 | |
| B. | 只要满足l3≥$\sqrt{({l}_{1}+h)^{2}+4{d}^{2}}$,糖果就能经过正下方第一颗星星处 | |
| C. | 糖果可能以$\frac{mg{{l}_{2}}^{2}}{{d}^{2}}$($\sqrt{{{l}_{2}}^{2}-{d}^{2}}$-l1)的初动能开始绕中间悬点做圆运动 | |
| D. | 糖果到达最低点的动能可能等于mg[l2-$\frac{({{l}_{2}}^{2}-{d}^{2})^{\frac{3}{2}}}{{{l}_{2}}^{2}}$-$\frac{{l}_{1}{d}^{2}}{{{l}_{2}}^{2}}$] |
5. 如图所示,半径为R的光滑圆环竖直放置,在环上套有小球A和B,A、B之间用一根长为2R的轻杆相连,并使小球能在环上自由滑动.已知A球质量为3m,B球质量为m,重力加速度为g,使小球从与圆心O等高处静止释放,在A球从初始位置滑到圆环最低点的过程中,轻杆对B球做的功为( )
如图所示,半径为R的光滑圆环竖直放置,在环上套有小球A和B,A、B之间用一根长为2R的轻杆相连,并使小球能在环上自由滑动.已知A球质量为3m,B球质量为m,重力加速度为g,使小球从与圆心O等高处静止释放,在A球从初始位置滑到圆环最低点的过程中,轻杆对B球做的功为( )
 如图所示,半径为R的光滑圆环竖直放置,在环上套有小球A和B,A、B之间用一根长为2R的轻杆相连,并使小球能在环上自由滑动.已知A球质量为3m,B球质量为m,重力加速度为g,使小球从与圆心O等高处静止释放,在A球从初始位置滑到圆环最低点的过程中,轻杆对B球做的功为( )
如图所示,半径为R的光滑圆环竖直放置,在环上套有小球A和B,A、B之间用一根长为2R的轻杆相连,并使小球能在环上自由滑动.已知A球质量为3m,B球质量为m,重力加速度为g,使小球从与圆心O等高处静止释放,在A球从初始位置滑到圆环最低点的过程中,轻杆对B球做的功为( )| A. | mgR | B. | 1.5mgR | C. | 2mgR | D. | 3mgR |
2.一定质量的气体,在体积不变的情况下,温度升高,压强增大的原因中,错误的是( )
| A. | 温度升高后,气体分子的平均速率变大 | |
| B. | 温度升高后,气体分子的平均动能变大 | |
| C. | 温度升高后,分子撞击器壁的平均作用力增大 | |
| D. | 温度升高后,单位体积内的分子数增多,撞击到单位面积器壁上的分子数增多了 |

 如图所示,弹簧一端固定于水平台面上,另一端与质量为m活塞栓接在一起,开口向下.质量为M的气缸与活塞一起封闭了一定质量的气体,气缸和活塞均可与外界进行热交换.由于外界环境的温度缓慢降低,被封闭气体向外界释放热量Q,同时其内能减少△U,已知大气压强为P0,气缸的横截面积为S,气缸壁厚忽略不计,重力加速度为g,则:
如图所示,弹簧一端固定于水平台面上,另一端与质量为m活塞栓接在一起,开口向下.质量为M的气缸与活塞一起封闭了一定质量的气体,气缸和活塞均可与外界进行热交换.由于外界环境的温度缓慢降低,被封闭气体向外界释放热量Q,同时其内能减少△U,已知大气压强为P0,气缸的横截面积为S,气缸壁厚忽略不计,重力加速度为g,则: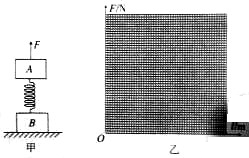 质量均为4kg的物体A、B用一劲度系数k=200N/m的轻质弹簧连接,将它们竖直静止放在水平面上,如图甲所示,现将一竖直向上的变力F作用在A上,使A开始向上做匀加速运动,经0.40s物体B刚要离开地面.取g=10m/s2
质量均为4kg的物体A、B用一劲度系数k=200N/m的轻质弹簧连接,将它们竖直静止放在水平面上,如图甲所示,现将一竖直向上的变力F作用在A上,使A开始向上做匀加速运动,经0.40s物体B刚要离开地面.取g=10m/s2 光滑斜面AB足够长,斜面倾角为θ=30°,斜面底端A处固定一挡板,现让物块1、2先后从A处以相同的初速度v=10m/s沿斜面向上运动,时间间隔T=2s,物块1、2质量分别为m1=2kg,m2=3kg.假设不考虑空气阻力,物块1、2间及物块2与挡板间的碰撞为弹性碰撞.且碰撞时间极短.g取10m/s2.求物块1、2第一次碰撞后瞬间各自的速度v1,v2.
光滑斜面AB足够长,斜面倾角为θ=30°,斜面底端A处固定一挡板,现让物块1、2先后从A处以相同的初速度v=10m/s沿斜面向上运动,时间间隔T=2s,物块1、2质量分别为m1=2kg,m2=3kg.假设不考虑空气阻力,物块1、2间及物块2与挡板间的碰撞为弹性碰撞.且碰撞时间极短.g取10m/s2.求物块1、2第一次碰撞后瞬间各自的速度v1,v2.