题目内容
2. 光滑斜面AB足够长,斜面倾角为θ=30°,斜面底端A处固定一挡板,现让物块1、2先后从A处以相同的初速度v=10m/s沿斜面向上运动,时间间隔T=2s,物块1、2质量分别为m1=2kg,m2=3kg.假设不考虑空气阻力,物块1、2间及物块2与挡板间的碰撞为弹性碰撞.且碰撞时间极短.g取10m/s2.求物块1、2第一次碰撞后瞬间各自的速度v1,v2.
光滑斜面AB足够长,斜面倾角为θ=30°,斜面底端A处固定一挡板,现让物块1、2先后从A处以相同的初速度v=10m/s沿斜面向上运动,时间间隔T=2s,物块1、2质量分别为m1=2kg,m2=3kg.假设不考虑空气阻力,物块1、2间及物块2与挡板间的碰撞为弹性碰撞.且碰撞时间极短.g取10m/s2.求物块1、2第一次碰撞后瞬间各自的速度v1,v2.
分析 物体沿光滑斜面上滑时做匀变速运动,由牛顿第二定律求得加速度.根据相遇时位移关系列式求出时间,再由速度公式求碰撞前两者的速度.对于碰撞,遵守动量守恒和动能守恒,由动量守恒定律和机械能守恒定律列式,可求出物块1、2第一次碰撞后瞬间各自的速度.
解答 解:两物块在斜面上运动的加速度大小均为 a=$\frac{mgsinθ}{m}$=gsinθ=5m/s2,方向沿斜面向下.
设物块2运动时间t后与物块1相遇,由运动学公式有:
vt-$\frac{1}{2}a{t}^{2}$=v(t+T)-$\frac{1}{2}a(t+T)^{2}$
规定沿斜面向上为正方向,设相遇时物块1、2的速度分别为v1′、v2′,由运动学公式有:
v1′=v-a(t+T)
v2′=v-at
碰撞过程中,由动量守恒定律和机械能守恒定律有:
m1v1′+m2v2′=m1v1+m2v2;
$\frac{1}{2}$m1v1′2+$\frac{1}{2}$m2v2′2=$\frac{1}{2}$m1v12+$\frac{1}{2}$m2v22;
联立解得:v1=7m/s,v2=-3m/s
答:物块1、2第一次碰撞后瞬间各自的速度v1、v2分别为7m/s,沿斜面向上和3m/s,沿斜面向下.
点评 解决本题的关键要抓住相遇时的位移关系,运用运动学公式求出时间.对于弹性碰撞,要抓住两大守恒定律:动量守恒定律和机械能守恒定律,注意选取正方向.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
16.下列物理量属于矢量的是( )
| A. | 电场强度E | B. | 电流强度I | C. | 功率P | D. | 周期T |
10. 如图所示,在网球的网前截击练习中,若练习者在球网正上方距地面H处,将球以速度v沿垂直球网的方向击出,球刚好落在底线上.已知球的质量为m,底线到网的距离为L,重力加速度为g,将球的运动视作平抛运动,下列叙述正确的是( )
如图所示,在网球的网前截击练习中,若练习者在球网正上方距地面H处,将球以速度v沿垂直球网的方向击出,球刚好落在底线上.已知球的质量为m,底线到网的距离为L,重力加速度为g,将球的运动视作平抛运动,下列叙述正确的是( )
 如图所示,在网球的网前截击练习中,若练习者在球网正上方距地面H处,将球以速度v沿垂直球网的方向击出,球刚好落在底线上.已知球的质量为m,底线到网的距离为L,重力加速度为g,将球的运动视作平抛运动,下列叙述正确的是( )
如图所示,在网球的网前截击练习中,若练习者在球网正上方距地面H处,将球以速度v沿垂直球网的方向击出,球刚好落在底线上.已知球的质量为m,底线到网的距离为L,重力加速度为g,将球的运动视作平抛运动,下列叙述正确的是( )| A. | 球的速度v等于L$\sqrt{\frac{g}{2H}}$ | |
| B. | 球从击球点至落地点的动能减少了$\frac{1}{2}$mv2 | |
| C. | 球从击球点至落地点的重力势能减少了mgH | |
| D. | 球从击球点至落地点的机械能减少了mgH+$\frac{1}{2}$mv2 |
14.某次军演飞机练习投弹实验中,甲乙两架飞机沿同向水平飞行的速度之比v甲:v乙=2:1,离地面的高度之比h甲:h乙=1:2,若要两飞机命中地面的同一目标,不计空气阻力,投弹时甲乙离目标的水平位移之比为( )
| A. | 1:2 | B. | 1:4 | C. | 1:$\sqrt{2}$ | D. | $\sqrt{2}$:1 |
11.下列说法正确的是( )
| A. | 物体受恒力作用,可能做匀速圆周运动,而做圆周运动,所受合外力却不一定指向圆心 | |
| B. | 做曲线运动速度方向一定时刻改变,而加速度方向不一定改变 | |
| C. | 平抛运动速度方向,速度变化量方向时刻改变,速度变化率方向不改变 | |
| D. | 物体受恒力作用可能先做减速曲线运动,直到速度最小值为零后做加速曲线运动 |
 如图所示,竖直平面内的光滑水平轨道的左边与墙壁对接,右边与一个足够高的$\frac{1}{4}$光滑圆孤轨道平滑相连.木块A、B静置于光滑水平轨道上,A、B的质量分别为1.5kg和0.5kg.现让A以5m/s的速度水平向左运动,之后与墙壁碰撞,碰撞的时间为0.3s,碰后的速度大小变为2m/s.当A与B碰撞后会立即粘在一起运动,g取10m/s2,求:
如图所示,竖直平面内的光滑水平轨道的左边与墙壁对接,右边与一个足够高的$\frac{1}{4}$光滑圆孤轨道平滑相连.木块A、B静置于光滑水平轨道上,A、B的质量分别为1.5kg和0.5kg.现让A以5m/s的速度水平向左运动,之后与墙壁碰撞,碰撞的时间为0.3s,碰后的速度大小变为2m/s.当A与B碰撞后会立即粘在一起运动,g取10m/s2,求: 如图是小飞同学在做“描绘小灯泡的伏安特性曲线”实验的实物连接图,根据题图在答题纸的方框中补全实验电路图.
如图是小飞同学在做“描绘小灯泡的伏安特性曲线”实验的实物连接图,根据题图在答题纸的方框中补全实验电路图.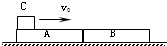 在光滑的水平面上,并排放置着两个质量为m、长L的完全相同的A、B长木板.一质量为2m的小滑块,以一定的初速度v0,从左侧冲上木板A,滑块与木板间的动摩擦因数为μ,要使滑块最终能停在木板B上,并以$\frac{5}{9}$v0的速度共同运动.重力加速度为g,求:
在光滑的水平面上,并排放置着两个质量为m、长L的完全相同的A、B长木板.一质量为2m的小滑块,以一定的初速度v0,从左侧冲上木板A,滑块与木板间的动摩擦因数为μ,要使滑块最终能停在木板B上,并以$\frac{5}{9}$v0的速度共同运动.重力加速度为g,求: