题目内容
3. 遥控赛车比赛中有一个规定项目:飞越“壕沟”.比赛要求:赛车从起点A由静止出发,沿水平直线轨道运动,在B点飞出后越过“壕沟”,落到平观EF段(如图所示).赛车通电后以额定功率P=1.5W工作,在AB段运动过程中,受到阻力恒为F1=0.3N,在空中运动的过程不计空气阻力.已知赛车质量m=0.1kg,AB的长度L=10.00m,BE的高度差h=1.25m,BE的水平距离s=1.50m.(重力加速度g=10m/s2).
遥控赛车比赛中有一个规定项目:飞越“壕沟”.比赛要求:赛车从起点A由静止出发,沿水平直线轨道运动,在B点飞出后越过“壕沟”,落到平观EF段(如图所示).赛车通电后以额定功率P=1.5W工作,在AB段运动过程中,受到阻力恒为F1=0.3N,在空中运动的过程不计空气阻力.已知赛车质量m=0.1kg,AB的长度L=10.00m,BE的高度差h=1.25m,BE的水平距离s=1.50m.(重力加速度g=10m/s2).(1)若赛车在AB轨道上能达到最大速度vm,求vm的大小;
(2)要使赛车完成比赛,赛车通电时间至少为多长?
分析 (1)赛车达到最大速度vm时,牵引力与阻力大小相等F=Ff又据P=Fv求解最大速度;
(2)通过平抛运动的轨道求出通过B点的速度,从而确定通过B点的最小速度,根据动能定理求出要使赛车完成比赛,电动机至少工作的时间.
解答 解:(1)赛车达到最大速度vm时,牵引力与阻力大小相等F=Ff
又据:P=Fv
解得:vm=$\frac{P}{f}$=$\frac{1.5}{0.3}$=5m/s
(2)设赛车越过壕沟需要的最小速度为v,由平抛运动的规律s=vt1…①
$h=\frac{1}{2}gt_1^2$…②
解①②得v=3m/s
设电动机工作时间至少为t2,
根据动能能定理得:$P{t_2}-{F_f}L=\frac{1}{2}m{v^2}$
1.5t2-0.3×10=$\frac{1}{2}$×0.1×32
由此可得:t2=2.3s
答:(1)若赛车在AB轨道上能达到最大速度vm为3m/s;
(2)要使赛车完成比赛,赛车通电时间至少2.3s.
点评 本题综合考查了动能定理、牛顿第二定律,涉及到直线运动、平抛运动,综合性较强,需加强这方面的训练.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
11.依据热学知识可知,下列说法正确的是( )
| A. | 已知一定质量物质的体积和该物质分子的体积,一定能估算出阿伏伽德罗常数 | |
| B. | 当分子力表现为斥力时,分子间距减小,分子势能将增大 | |
| C. | 要使一定质量的气体分子平均动能增大,外界一定向气体传热 | |
| D. | 外界对气体做功,气体压强增大,内能也增加 |
18. 如图所示,有两根和水平方向成θ角的光滑平行的金属轨道,上端接有可变电阻R,下端足够长,空间有垂直轨道平面的匀强磁场B,一根质量为m的金属杆MN从轨道上由静止滑下,经过足够长的时间后,流经金属棒的电流达到最大,金属杆做匀速运动,金属杆和轨道电阻均不计.则( )
如图所示,有两根和水平方向成θ角的光滑平行的金属轨道,上端接有可变电阻R,下端足够长,空间有垂直轨道平面的匀强磁场B,一根质量为m的金属杆MN从轨道上由静止滑下,经过足够长的时间后,流经金属棒的电流达到最大,金属杆做匀速运动,金属杆和轨道电阻均不计.则( )
 如图所示,有两根和水平方向成θ角的光滑平行的金属轨道,上端接有可变电阻R,下端足够长,空间有垂直轨道平面的匀强磁场B,一根质量为m的金属杆MN从轨道上由静止滑下,经过足够长的时间后,流经金属棒的电流达到最大,金属杆做匀速运动,金属杆和轨道电阻均不计.则( )
如图所示,有两根和水平方向成θ角的光滑平行的金属轨道,上端接有可变电阻R,下端足够长,空间有垂直轨道平面的匀强磁场B,一根质量为m的金属杆MN从轨道上由静止滑下,经过足够长的时间后,流经金属棒的电流达到最大,金属杆做匀速运动,金属杆和轨道电阻均不计.则( )| A. | 下滑过程中,金属杆中的电流方向为从M到N | |
| B. | 加速运动过程中,金属杆克服安培力做的功大于可变电阻R的产生的焦耳热 | |
| C. | 匀速运动过程中,金属杆的重力功率等于可变电阻R的发热功率 | |
| D. | 若R增大,流经金属棒的最大电流将减小 |
15. 如图所示,质量为m的物体静止在地面上,物体上边连着一个轻质弹簧,弹簧的劲度系数为K,用手拉住弹簧上端,使物体缓缓提高H,不计弹簧质量,则人做的功( )
如图所示,质量为m的物体静止在地面上,物体上边连着一个轻质弹簧,弹簧的劲度系数为K,用手拉住弹簧上端,使物体缓缓提高H,不计弹簧质量,则人做的功( )
 如图所示,质量为m的物体静止在地面上,物体上边连着一个轻质弹簧,弹簧的劲度系数为K,用手拉住弹簧上端,使物体缓缓提高H,不计弹簧质量,则人做的功( )
如图所示,质量为m的物体静止在地面上,物体上边连着一个轻质弹簧,弹簧的劲度系数为K,用手拉住弹簧上端,使物体缓缓提高H,不计弹簧质量,则人做的功( )| A. | 小于mgH | B. | 等于mgH | ||
| C. | 大于mgH | D. | 以上情况皆有可能 |
12. 如图所示,弧光灯发出的光经一狭缝后,在锌板上形成明暗相间的条纹,与锌板相连的验电器的铝箔有张角,则该实验能证明 ( )
如图所示,弧光灯发出的光经一狭缝后,在锌板上形成明暗相间的条纹,与锌板相连的验电器的铝箔有张角,则该实验能证明 ( )
(1)弧光灯发出的光具有波动性
(2)锌板上带电
(3)光通过狭缝时发生了衍射
(4)微观粒子具有波动性.
 如图所示,弧光灯发出的光经一狭缝后,在锌板上形成明暗相间的条纹,与锌板相连的验电器的铝箔有张角,则该实验能证明 ( )
如图所示,弧光灯发出的光经一狭缝后,在锌板上形成明暗相间的条纹,与锌板相连的验电器的铝箔有张角,则该实验能证明 ( )(1)弧光灯发出的光具有波动性
(2)锌板上带电
(3)光通过狭缝时发生了衍射
(4)微观粒子具有波动性.
| A. | (1)(2)(3) | B. | (3)(4) | C. | (1)(3) | D. | (2)(4) |
13.下列说法中正确的是( )
| A. | 只有体积很小的电荷才能看成点电荷 | |
| B. | 任何带电体的带电量一定是元电荷电量的整数倍 | |
| C. | 以场源电荷为圆心的圆周上各点电场强度相同 | |
| D. | 检验电荷的电性改变,所在位置的场强方向不发生改变 |
 如图所示,在第一象限存在匀强电场,场强沿y轴负方向;在第二象限有两块平行金属板M、N组成的加速电场,板间的电压为U.一电荷量为+q、质量为m的带电粒子,靠近M板由静止释放,经N板小孔沿x轴正方向飞出,经过y轴上y=h处的点P1进入匀强电场,然后,在经过x轴上P2点进入第四象限时其速度与x轴正方向的夹角θ=53°,不计粒子的重力,已知sin53°=0.8,cos53°=0.6,求:
如图所示,在第一象限存在匀强电场,场强沿y轴负方向;在第二象限有两块平行金属板M、N组成的加速电场,板间的电压为U.一电荷量为+q、质量为m的带电粒子,靠近M板由静止释放,经N板小孔沿x轴正方向飞出,经过y轴上y=h处的点P1进入匀强电场,然后,在经过x轴上P2点进入第四象限时其速度与x轴正方向的夹角θ=53°,不计粒子的重力,已知sin53°=0.8,cos53°=0.6,求:


 .
.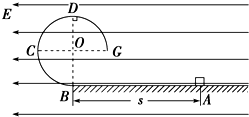 如图所示,BCDG是光滑绝缘的$\frac{3}{4}$圆形轨道,位于竖直平面内,轨道半径为R,下端与水平绝缘轨道在B点平滑连接,整个轨道处在水平向左的匀强电场中.现有一质量为m、带正电的小滑块(可视为质点)置于水平轨道上,滑块受到的电场力大小为$\frac{3}{4}$mg,滑块与水平轨道间的动摩擦因数为0.5,重力加速度为g.
如图所示,BCDG是光滑绝缘的$\frac{3}{4}$圆形轨道,位于竖直平面内,轨道半径为R,下端与水平绝缘轨道在B点平滑连接,整个轨道处在水平向左的匀强电场中.现有一质量为m、带正电的小滑块(可视为质点)置于水平轨道上,滑块受到的电场力大小为$\frac{3}{4}$mg,滑块与水平轨道间的动摩擦因数为0.5,重力加速度为g.