题目内容
8. 如图所示,让质量为m=0.2kg图中的位置A由静止开始下摆,正好摆到最低点B时摆线被拉断.设摆线长l=1.5m,悬点到地面的高度为h=6.5m,不计空气阻力.(g=10m/s2)
如图所示,让质量为m=0.2kg图中的位置A由静止开始下摆,正好摆到最低点B时摆线被拉断.设摆线长l=1.5m,悬点到地面的高度为h=6.5m,不计空气阻力.(g=10m/s2)(1)摆球运动至B点时的速率v;
(2)绳子所能承受的最大拉力T;
(3)摆球落地的速度大小.
分析 (1)摆球由A位置摆到最低点B位置的过程中,只有重力对摆球做功,其机械能守恒.由机械能守恒定律求出摆球摆到最低点B位置时的速度.
(2)摆球经过B位置时由重力和细线的拉力提供向心力,根据牛顿第二定律求解细线的拉力.
(3)根据动能定理求出落地时的速度.
解答 解:(1)摆球由A位置摆到最低点B位置的过程中,由机械能守恒得:
mg(L-L cos37°)=$\frac{1}{2}m{v}^{2}$
解得:v=$\sqrt{6}m/s$
(2)球经B点时,由牛顿第二定律有:
T-mg=m$\frac{{v}^{2}}{l}$
解得:
T=2.8N
(3)从B到C的过程中,根据动能定理得:
$\frac{1}{2}m{{v}_{C}}^{2}-\frac{1}{2}m{v}^{2}=mg(h-L)$
解得:${v}_{C}=\sqrt{106}$m/s
答:(1)摆球运动至B点时的速率v为$\sqrt{6}m/s$;
(2)绳子所能承受的最大拉力T为2.8N;
(3)摆球落地的速度大小为$\sqrt{106}$m/s.
点评 本题是圆周运动与平抛运动的综合,采用程序法分析求解.两个过程机械能都守恒.属于基础题.

练习册系列答案
相关题目
18.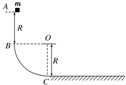 如图所示,BC是竖直面内的四分之一圆弧形光滑轨道,下端C与水平直轨道相切.一个小物块从B点正上方R处的A点处由静止释放,从B点刚好进入圆弧形光滑轨道下滑,已知圆弧形轨道半径为R=0.2m,小物块的质量为m=0.1kg,小物块与水平面间的动摩擦因数μ=0.5,取g=10m/s2.小物块在水平面上滑动的最大距离是( )
如图所示,BC是竖直面内的四分之一圆弧形光滑轨道,下端C与水平直轨道相切.一个小物块从B点正上方R处的A点处由静止释放,从B点刚好进入圆弧形光滑轨道下滑,已知圆弧形轨道半径为R=0.2m,小物块的质量为m=0.1kg,小物块与水平面间的动摩擦因数μ=0.5,取g=10m/s2.小物块在水平面上滑动的最大距离是( )
 如图所示,BC是竖直面内的四分之一圆弧形光滑轨道,下端C与水平直轨道相切.一个小物块从B点正上方R处的A点处由静止释放,从B点刚好进入圆弧形光滑轨道下滑,已知圆弧形轨道半径为R=0.2m,小物块的质量为m=0.1kg,小物块与水平面间的动摩擦因数μ=0.5,取g=10m/s2.小物块在水平面上滑动的最大距离是( )
如图所示,BC是竖直面内的四分之一圆弧形光滑轨道,下端C与水平直轨道相切.一个小物块从B点正上方R处的A点处由静止释放,从B点刚好进入圆弧形光滑轨道下滑,已知圆弧形轨道半径为R=0.2m,小物块的质量为m=0.1kg,小物块与水平面间的动摩擦因数μ=0.5,取g=10m/s2.小物块在水平面上滑动的最大距离是( )| A. | 0.1m | B. | 0.2m | C. | 0.6m | D. | 0.8m |
19.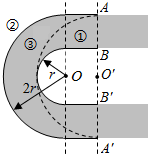 如图所示为赛车场的一个水平“U”形弯道,转弯处为圆心在O点的半圆,内外半径分别为r和2r,一辆质量为m的赛车通过AB线经弯道到达A′B′线,有如图所示的①、②、③三条路线,其中路线③是以O′为圆心的半圆,OO′=r,赛车沿圆弧路线行驶时,路面对轮胎的最大径向静摩擦力为Fmax,选择路线,赛车以不打滑的最大速率通过弯道(所选路线内赛车速率不变,发动机功率足够大),则( )
如图所示为赛车场的一个水平“U”形弯道,转弯处为圆心在O点的半圆,内外半径分别为r和2r,一辆质量为m的赛车通过AB线经弯道到达A′B′线,有如图所示的①、②、③三条路线,其中路线③是以O′为圆心的半圆,OO′=r,赛车沿圆弧路线行驶时,路面对轮胎的最大径向静摩擦力为Fmax,选择路线,赛车以不打滑的最大速率通过弯道(所选路线内赛车速率不变,发动机功率足够大),则( )
 如图所示为赛车场的一个水平“U”形弯道,转弯处为圆心在O点的半圆,内外半径分别为r和2r,一辆质量为m的赛车通过AB线经弯道到达A′B′线,有如图所示的①、②、③三条路线,其中路线③是以O′为圆心的半圆,OO′=r,赛车沿圆弧路线行驶时,路面对轮胎的最大径向静摩擦力为Fmax,选择路线,赛车以不打滑的最大速率通过弯道(所选路线内赛车速率不变,发动机功率足够大),则( )
如图所示为赛车场的一个水平“U”形弯道,转弯处为圆心在O点的半圆,内外半径分别为r和2r,一辆质量为m的赛车通过AB线经弯道到达A′B′线,有如图所示的①、②、③三条路线,其中路线③是以O′为圆心的半圆,OO′=r,赛车沿圆弧路线行驶时,路面对轮胎的最大径向静摩擦力为Fmax,选择路线,赛车以不打滑的最大速率通过弯道(所选路线内赛车速率不变,发动机功率足够大),则( )| A. | 选择路线①,赛车经过的路程最短 | |
| B. | 选择路线②,赛车的速率最小 | |
| C. | 选择路线③,赛车所用时间最短 | |
| D. | ①、②、③三条路线的圆弧上,赛车的向心加速度大小相等 |
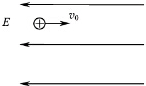
16.一带正电的小球向右水平抛入范围足够大的匀强电场,电场方向水平向左,不计空气阻力,则小球( )

| A. | 做直线运动 | B. | 做曲线运动 | ||
| C. | 速率先减小后增大 | D. | 速率先增大后减小 |
1.关于向心加速度的物理意义,下列说法中正确的是( )
| A. | 它只改变线速度的方向 | |
| B. | 它描述的是线速度大小变化的快慢 | |
| C. | 它描述的是角速度变化的快慢 | |
| D. | 匀速圆周运动的向心加速度是恒定不变的 |
18.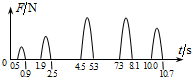 为了测量蹦床运动员从蹦床上跃起的高度,探究小组设计了如下的方法:在蹦床的弹性网上安装压力传感器,利用传感器记录运动员在运动过程中对弹性网的压力,来推测运动员跃起的高度.图为某段时间内蹦床的压力-时间图象.不计空气阻力,运动员仅在竖直方向上运动,且可视为质点,则可估算出运动员在这段时间内跃起的最大高度为(g取10m/s2)( )
为了测量蹦床运动员从蹦床上跃起的高度,探究小组设计了如下的方法:在蹦床的弹性网上安装压力传感器,利用传感器记录运动员在运动过程中对弹性网的压力,来推测运动员跃起的高度.图为某段时间内蹦床的压力-时间图象.不计空气阻力,运动员仅在竖直方向上运动,且可视为质点,则可估算出运动员在这段时间内跃起的最大高度为(g取10m/s2)( )
 为了测量蹦床运动员从蹦床上跃起的高度,探究小组设计了如下的方法:在蹦床的弹性网上安装压力传感器,利用传感器记录运动员在运动过程中对弹性网的压力,来推测运动员跃起的高度.图为某段时间内蹦床的压力-时间图象.不计空气阻力,运动员仅在竖直方向上运动,且可视为质点,则可估算出运动员在这段时间内跃起的最大高度为(g取10m/s2)( )
为了测量蹦床运动员从蹦床上跃起的高度,探究小组设计了如下的方法:在蹦床的弹性网上安装压力传感器,利用传感器记录运动员在运动过程中对弹性网的压力,来推测运动员跃起的高度.图为某段时间内蹦床的压力-时间图象.不计空气阻力,运动员仅在竖直方向上运动,且可视为质点,则可估算出运动员在这段时间内跃起的最大高度为(g取10m/s2)( )| A. | 3.2m | B. | 5.0m | C. | 6.4m | D. | 10.0m |
19.某学习小组欲探究小灯泡(额定电压为3V,额定电流约为0.5A)的伏安特性,可提供的实验器材如下:
A.干电池:电动势约4.5V,内阻可不计
B.双量程的电压表V1:量程为0~3V、内阻约为3kΩ;V2:量程为0~15V、内阻约为15kΩ
C.双量程的电流表 A1:量程为0~0.6A、内阻约为1Ω;A2:量程为0~3A、内阻约为0.1Ω
D.滑动变阻器R:阻值范围0~10Ω、允许通过最大电流为2A
E.开关S,导线若干
在尽量提高测量精度的情况下,请回答下列问题:
①根据以上器材,请你把实验电路原理图1补充完整,并在图1中标明所选器材的代号.
②根据选择的正确电路原理图,用笔画线代替导线将实物图2连接成完整电路.闭合开关前,滑动变阻器的滑动片应移到A端(选填“A”或“B”)

③按正确操作得到7组电压表和电流表示数如表所示,请图3所示的坐标纸上画出小灯泡的U-I图线.
④若将该小灯泡接在电动势为3.0V、内阻为2.0Ω的干电池两端,则此时该小灯泡的电阻为4.6Ω.(结果保留3个有效数字)
A.干电池:电动势约4.5V,内阻可不计
B.双量程的电压表V1:量程为0~3V、内阻约为3kΩ;V2:量程为0~15V、内阻约为15kΩ
C.双量程的电流表 A1:量程为0~0.6A、内阻约为1Ω;A2:量程为0~3A、内阻约为0.1Ω
D.滑动变阻器R:阻值范围0~10Ω、允许通过最大电流为2A
E.开关S,导线若干
在尽量提高测量精度的情况下,请回答下列问题:
①根据以上器材,请你把实验电路原理图1补充完整,并在图1中标明所选器材的代号.
②根据选择的正确电路原理图,用笔画线代替导线将实物图2连接成完整电路.闭合开关前,滑动变阻器的滑动片应移到A端(选填“A”或“B”)

③按正确操作得到7组电压表和电流表示数如表所示,请图3所示的坐标纸上画出小灯泡的U-I图线.
| 组数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| U/V | 0 | 0.28 | 0.58 | 0.92 | 1.50 | 2.00 | 3.00 |
| I/A | 0 | 0.10 | 0.20 | 0.30 | 0.40 | 0.45 | 0.49 |
 图为某种离子加速器的设计方案.两个半圆形金属盒内存在相同的垂直于纸面向外的匀强磁场.其中MN和M′N′是间距为h的两平行极板,其上分别有正对的两个小孔O和O′,O′N′=ON=d,P为靶点,O′P=kd(k为大于1的整数).极板间存在方向向上的匀强电场,两极板间电压为U.质量为m、带电量为q的正离子从O点由静止开始加速,经O′进入磁场区域.当离子打到极板上O′N′区域(含N′点)或外壳上时将会被吸收.两虚线之间的区域无电场和磁场存在,离子可匀速穿过.忽略相对论效应和离子所受的重力.求:
图为某种离子加速器的设计方案.两个半圆形金属盒内存在相同的垂直于纸面向外的匀强磁场.其中MN和M′N′是间距为h的两平行极板,其上分别有正对的两个小孔O和O′,O′N′=ON=d,P为靶点,O′P=kd(k为大于1的整数).极板间存在方向向上的匀强电场,两极板间电压为U.质量为m、带电量为q的正离子从O点由静止开始加速,经O′进入磁场区域.当离子打到极板上O′N′区域(含N′点)或外壳上时将会被吸收.两虚线之间的区域无电场和磁场存在,离子可匀速穿过.忽略相对论效应和离子所受的重力.求: