题目内容
在圆形磁场区域的磁场强度为B，一群速率为v的不计重力的带正电的粒子自M点沿半径方向射入磁场区域，已知磁场区域的半径为r，粒子飞出磁场区域时偏角为60，求：（1）粒子的回旋半径R=？
（2）粒子在磁场中运动时间t=？
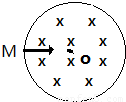
【答案】分析：（1）带电粒子进入磁场后受到洛伦兹力作用而做匀速圆周运动，作出轨迹，根据粒子速度的偏向角等于轨迹的圆心角，即可得到轨迹的圆心角为60°，由几何知识求出轨迹的半径．
（2）粒子在磁场中运动时间t=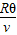
，R是粒子轨迹半径，θ是轨迹的圆心角．
解答：
解：（1）带电粒子进入磁场后受到洛伦兹力作用而做匀速圆周运动，作出轨迹如图，由推论得知：粒子速度的偏向角等于轨迹的圆心角，则得轨迹对应的圆心角θ=60°，由几何知识得：轨迹的半径为：R=rtan60°=
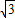r．
（2）粒子在磁场中运动时间：t=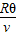
=
=
．
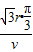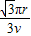答：
（1）粒子的回旋半径R为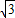
r．
（2）粒子在磁场中运动时间t为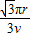
．
点评：本题容易出错的地方是将磁场范围半径与粒子轨迹半径混淆，死记公式r=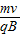
．
（2）粒子在磁场中运动时间t=
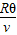，R是粒子轨迹半径，θ是轨迹的圆心角．解答：
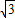解：（1）带电粒子进入磁场后受到洛伦兹力作用而做匀速圆周运动，作出轨迹如图，由推论得知：粒子速度的偏向角等于轨迹的圆心角，则得轨迹对应的圆心角θ=60°，由几何知识得：轨迹的半径为：R=rtan60°=r．（2）粒子在磁场中运动时间：t=
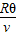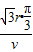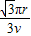==．答：
（1）粒子的回旋半径R为
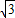r．（2）粒子在磁场中运动时间t为
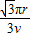．点评：本题容易出错的地方是将磁场范围半径与粒子轨迹半径混淆，死记公式r=
． 
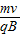练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
在半径为r的圆形区域内有一匀强磁场，磁场方向如图所示．一束速度不同的质子从磁场边缘的A点沿直径方向飞入磁场后，经不同路径飞出磁场，其中有三个质子分别到达磁场边缘的a，b，c三点．若不计质子间的相互作用力，比较这三个质子的运动情况，下面说法正确的是（ ）
在xOy平面上，一个以原点O为圆心，半径为4R的圆形磁场区域内存在着匀强磁场，磁场的方向垂直于纸面向里，在坐标为（-2R，0）的A处静止着一个具有放射性的原子核一氮（
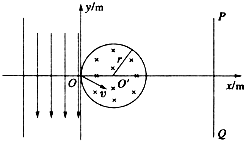如图所示，在xOy平面内，y轴左侧有一个方向竖直向下，水平宽度为