题目内容
8.如图甲所示,在水平面上固定一个匝数为10匝的等边三角形金属线框,总电阻为3Ω,边长为0.4m.金属框处于两个半径为0.1m的圆形匀强磁场中,顶点A恰好位于左边圆的圆心,BC边的中点恰好与右边圆的圆心重合.左边磁场方向垂直水平面向外,右边磁场垂直水平面向里,磁感应强度的变化规律如图乙所示,则下列说法中正确的是(π取3)( )
| A. | 线框中感应电流的方向是顺时针方向 | |
| B. | t=0.4s时,穿过线框的磁通量为0.005Wb | |
| C. | 经过t=0.4s,线框中产生的热量为0.3J | |
| D. | 前0.4s内流过线框的电量为0.2C |
分析 根据楞次定律判断感应电流的方向;根据磁通量Φ=BS求解;由q=$\overline{I}$t=$\frac{\overline{E}}{R}$t求解电荷量;由Q=I2Rt求解热量.
解答 解:A、由磁感应强度B1垂直水平面向里,大小随时间增大;B2垂直水平面向外,大小不变,故线框的磁通量增大,由楞次定律可得,线框中感应电流方向为逆时针方向,故A错误;
B、t=0.4s时刻穿过线框的磁通量为:
∅=B1×$\frac{1}{2}$×πr2-B2×$\frac{1}{6}$×πr2=5×0.5×3×0.12-4×$\frac{1}{6}$×3×0.12Wb=0.055Wb,故B错误;
C、由Q=I2Rt=($\frac{n△∅}{△t}$)2×$\frac{1}{R}$×△t=($\frac{10×(5-1)×\frac{1}{2}π×0.{1}^{2}}{0.4}$)2×$\frac{1}{3}$×0.4J=0.3J,故C正确;
D、在t=0.4s内通过线框中的电量q=$\overline{I}$t=$\frac{\overline{E}}{R}$t=$\frac{n△∅}{R}$=10×$\frac{5-1}{3}×\frac{1}{2}×π×0.{1}^{2}$C=0.2C,故D正确.
故选:CD.
点评 考查磁通量的定义,注意磁通量的正负,理解法拉第电磁感应定律与闭合电路欧姆定律的应用,及其焦耳定律,注意安培力大小计算与方向的判定.

练习册系列答案
相关题目
18. 如图所示是一列沿x轴传播的简谐横波在某时刻的波形图,已知质点a的运动状态总是滞后于质点b的运动状态0.5s,质点b和质点c之间的距离是5cm,下列说法中正确的是( )
如图所示是一列沿x轴传播的简谐横波在某时刻的波形图,已知质点a的运动状态总是滞后于质点b的运动状态0.5s,质点b和质点c之间的距离是5cm,下列说法中正确的是( )
 如图所示是一列沿x轴传播的简谐横波在某时刻的波形图,已知质点a的运动状态总是滞后于质点b的运动状态0.5s,质点b和质点c之间的距离是5cm,下列说法中正确的是( )
如图所示是一列沿x轴传播的简谐横波在某时刻的波形图,已知质点a的运动状态总是滞后于质点b的运动状态0.5s,质点b和质点c之间的距离是5cm,下列说法中正确的是( )| A. | 此列波沿x轴正方向传播x | B. | 此列波的频率为2Hz | ||
| C. | 此列波的波长为10cm | D. | 此列波的传播速度为5cm/s |
19. 如图所示,光滑绝缘细管与水平面成30°角,在管的右上方P点固定一个点电荷+Q,P点与细管在同一竖直平面内,管的顶端A与P点连线水平.图中PB垂直AC,B是AC的中点,带电荷量为-q的小球(小球直径略小于细管的内径)从管中A处由静止开始沿管向下运动,它在A处时的加速度为a.不考虑小球电荷量对+Q形成的电场的影响.则在电场中( )
如图所示,光滑绝缘细管与水平面成30°角,在管的右上方P点固定一个点电荷+Q,P点与细管在同一竖直平面内,管的顶端A与P点连线水平.图中PB垂直AC,B是AC的中点,带电荷量为-q的小球(小球直径略小于细管的内径)从管中A处由静止开始沿管向下运动,它在A处时的加速度为a.不考虑小球电荷量对+Q形成的电场的影响.则在电场中( )
 如图所示,光滑绝缘细管与水平面成30°角,在管的右上方P点固定一个点电荷+Q,P点与细管在同一竖直平面内,管的顶端A与P点连线水平.图中PB垂直AC,B是AC的中点,带电荷量为-q的小球(小球直径略小于细管的内径)从管中A处由静止开始沿管向下运动,它在A处时的加速度为a.不考虑小球电荷量对+Q形成的电场的影响.则在电场中( )
如图所示,光滑绝缘细管与水平面成30°角,在管的右上方P点固定一个点电荷+Q,P点与细管在同一竖直平面内,管的顶端A与P点连线水平.图中PB垂直AC,B是AC的中点,带电荷量为-q的小球(小球直径略小于细管的内径)从管中A处由静止开始沿管向下运动,它在A处时的加速度为a.不考虑小球电荷量对+Q形成的电场的影响.则在电场中( )| A. | A点的电势高于B点的电势 | |
| B. | B点的电场强度大小是A点的4倍 | |
| C. | 小球运动到C处的加速度为$\frac{g}{2}$-a | |
| D. | 小球从A到C的过程中电势能先减小后增大 |
3.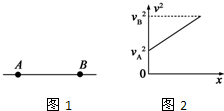 如图1所示,直线AB是某电场中的一条电场线,一电子仅在电场力作用下,由电场线上A点沿直线运动到B点,其速度平方v2与位移x的关系如图2所示.以下判断正确的是( )
如图1所示,直线AB是某电场中的一条电场线,一电子仅在电场力作用下,由电场线上A点沿直线运动到B点,其速度平方v2与位移x的关系如图2所示.以下判断正确的是( )
 如图1所示,直线AB是某电场中的一条电场线,一电子仅在电场力作用下,由电场线上A点沿直线运动到B点,其速度平方v2与位移x的关系如图2所示.以下判断正确的是( )
如图1所示,直线AB是某电场中的一条电场线,一电子仅在电场力作用下,由电场线上A点沿直线运动到B点,其速度平方v2与位移x的关系如图2所示.以下判断正确的是( )| A. | A点场强小于B点场强 | |
| B. | A点的电势低于B点的电势 | |
| C. | 电子从A点运动到B点,电场力做负功 | |
| D. | 电子在A点的电势能小于在B点的电势能 |
13. 一条弹性绳子呈水平状态,M为绳子中点,两端P、Q同时开始上下振动,一小段时间后产生的波形如图所示,对于其后绳上各点的振动情况,以下判断正确的是( )
一条弹性绳子呈水平状态,M为绳子中点,两端P、Q同时开始上下振动,一小段时间后产生的波形如图所示,对于其后绳上各点的振动情况,以下判断正确的是( )
 一条弹性绳子呈水平状态,M为绳子中点,两端P、Q同时开始上下振动,一小段时间后产生的波形如图所示,对于其后绳上各点的振动情况,以下判断正确的是( )
一条弹性绳子呈水平状态,M为绳子中点,两端P、Q同时开始上下振动,一小段时间后产生的波形如图所示,对于其后绳上各点的振动情况,以下判断正确的是( )| A. | 两列波将同时到达中点M | |
| B. | 两列波波速之比为1:2 | |
| C. | 中点M的振动总是加强的 | |
| D. | M点的位移大小在某时刻可能为零 | |
| E. | 绳的两端点P、Q开始振动的方向相同 |
20. 如图所示,A、B是竖直放置的平行板电容器的两个极板,与二极管D和电流连成电路,在平行板电容器A、B板间,有一带电小球悬挂且处于静止状态,现缓慢改变A、B两板间的距离,下列说法正确的是( )
如图所示,A、B是竖直放置的平行板电容器的两个极板,与二极管D和电流连成电路,在平行板电容器A、B板间,有一带电小球悬挂且处于静止状态,现缓慢改变A、B两板间的距离,下列说法正确的是( )
 如图所示,A、B是竖直放置的平行板电容器的两个极板,与二极管D和电流连成电路,在平行板电容器A、B板间,有一带电小球悬挂且处于静止状态,现缓慢改变A、B两板间的距离,下列说法正确的是( )
如图所示,A、B是竖直放置的平行板电容器的两个极板,与二极管D和电流连成电路,在平行板电容器A、B板间,有一带电小球悬挂且处于静止状态,现缓慢改变A、B两板间的距离,下列说法正确的是( )| A. | 增大两板间的距离,悬线与竖直方向的夹角不变 | |
| B. | 增大两板间的距离,悬线与竖直方向的夹角减小 | |
| C. | 减小两板间的距离,悬线与竖直方向的夹角增大 | |
| D. | 减小两板间的距离,悬线与竖直方向的夹角减小 |
17. 如图所示,足够长的平行金属导轨宽度为L=1m,与水平面间的倾角为兹=37°,导轨电阻不计,底端接有阻值为R=3Ω的定值电阻,磁感应强度为B=1T的匀强磁场垂直导轨平面向上穿过.有一质量为m=1kg、长也为L的导体棒始终与导轨垂直且接触良好,导体棒的电阻为R0=1Ω,它与导轨之间的动摩擦因数为μ=0.5.现让导体棒从导轨底部以平行斜面的速度v0=10m/s向上滑行,上滑的最大距离为s=4m(sin37°=0.6,cos37°=0.8,g=10m/s2).以下说法正确的是( )
如图所示,足够长的平行金属导轨宽度为L=1m,与水平面间的倾角为兹=37°,导轨电阻不计,底端接有阻值为R=3Ω的定值电阻,磁感应强度为B=1T的匀强磁场垂直导轨平面向上穿过.有一质量为m=1kg、长也为L的导体棒始终与导轨垂直且接触良好,导体棒的电阻为R0=1Ω,它与导轨之间的动摩擦因数为μ=0.5.现让导体棒从导轨底部以平行斜面的速度v0=10m/s向上滑行,上滑的最大距离为s=4m(sin37°=0.6,cos37°=0.8,g=10m/s2).以下说法正确的是( )
 如图所示,足够长的平行金属导轨宽度为L=1m,与水平面间的倾角为兹=37°,导轨电阻不计,底端接有阻值为R=3Ω的定值电阻,磁感应强度为B=1T的匀强磁场垂直导轨平面向上穿过.有一质量为m=1kg、长也为L的导体棒始终与导轨垂直且接触良好,导体棒的电阻为R0=1Ω,它与导轨之间的动摩擦因数为μ=0.5.现让导体棒从导轨底部以平行斜面的速度v0=10m/s向上滑行,上滑的最大距离为s=4m(sin37°=0.6,cos37°=0.8,g=10m/s2).以下说法正确的是( )
如图所示,足够长的平行金属导轨宽度为L=1m,与水平面间的倾角为兹=37°,导轨电阻不计,底端接有阻值为R=3Ω的定值电阻,磁感应强度为B=1T的匀强磁场垂直导轨平面向上穿过.有一质量为m=1kg、长也为L的导体棒始终与导轨垂直且接触良好,导体棒的电阻为R0=1Ω,它与导轨之间的动摩擦因数为μ=0.5.现让导体棒从导轨底部以平行斜面的速度v0=10m/s向上滑行,上滑的最大距离为s=4m(sin37°=0.6,cos37°=0.8,g=10m/s2).以下说法正确的是( )| A. | 导体棒滑行的整个过程中,它所受合力大小一直都在减小 | |
| B. | 导体棒最终可以匀速下滑到导轨底部 | |
| C. | 当导体棒向上滑行距离d=2m时,速度一定小于5$\sqrt{2}$m/s | |
| D. | 导体棒向上滑行的过程中,定值电阻R上产生的焦耳热为10J |
18.下列说法中与物理学史实相符的是( )
| A. | 牛顿认为力是改变物体运动状态的原因 | |
| B. | 亚里士多德认为力是维持物体运动的原因 | |
| C. | 笛卡尔通过扭秤实验第一个测出万有引力常量G的值 | |
| D. | 伽利略通过实验及合理外推,指出自由落体运动是一种匀变速直线运动 |
