题目内容
4. 如图所示,顶角为90°的“∨”型光滑金属导轨MON固定在倾角为θ的绝缘斜面上,M、N连线平行于斜面底端,导轨MO、NO的长度相等,M、N两点间的距离L=2m,整个装置处于磁感应强度大小B=0.5T、方向垂直于斜面向下的匀强磁场中.一根质量m=0.4kg,粗细均匀、单位长度电阻值r=0.5Ω/m的导体棒ab,受到平行于斜面向上且垂直于ab的变力F作用,以速度v=2m/s沿导轨向下匀速滑动.导体棒在运动过程中始终与导轨接触良好,不计导轨电阻,从导体棒在MN时开始计时.求:
如图所示,顶角为90°的“∨”型光滑金属导轨MON固定在倾角为θ的绝缘斜面上,M、N连线平行于斜面底端,导轨MO、NO的长度相等,M、N两点间的距离L=2m,整个装置处于磁感应强度大小B=0.5T、方向垂直于斜面向下的匀强磁场中.一根质量m=0.4kg,粗细均匀、单位长度电阻值r=0.5Ω/m的导体棒ab,受到平行于斜面向上且垂直于ab的变力F作用,以速度v=2m/s沿导轨向下匀速滑动.导体棒在运动过程中始终与导轨接触良好,不计导轨电阻,从导体棒在MN时开始计时.求:(1)t=0时,F=0,求斜面倾角θ;
(2)求0.2s内通过导体棒的电荷量q;
(3)求0.2S时导体棒所受外力F的功率.
分析 (1)导体棒匀速运动,沿斜面方向列出平衡方程,导体棒切割磁感线产生的感应电流为I,根据I=$\frac{E}{L×r}$ E=BLV可以求出I,就可以求出斜面倾角θ.
(2)导体棒的电荷量为q,根据q=It就可以求出电荷量q.
(3)沿斜面方向根据平衡方程可以求出外力F,根据功率P=Fv,就可以求出外力的功率.
解答 解:(1)导体棒开始运动时,回路中产生的感应电动势E=BLv
感应电流$I=\frac{E}{L•r}=\frac{Bv}{r}$
导体棒匀速运动,沿斜面方向:mgsinθ=BIL
代入数据得:0.4×10×sinθ=0.5×$\frac{0.5×2×2}{2×0.5}$×2
解得:$sinθ=\frac{1}{2}$,即θ=300
(2)由(1)知感应电流与导体棒的切割有效长度L无关
导体棒中的电流为I,则I=$\frac{E}{L×r}$=$\frac{BLV}{L×r}$=$\frac{BV}{r}$=2A
故0.2s内通过导体棒的电荷量为q=It=0.4C
(3)设导体棒经t时间沿导轨匀速向下运动的位移为x,
运动t=0.2s向下运动的位移为x=vt=0.4m
由几何关系可以求出此时切割的有效长度为l=1.2m
又mgsinθ=BIL+F
代入数据得:0.4×10×$\frac{1}{2}$=0.5×2×1.2+F
解得F=0.8N
外力F的功率为P,则P=Fv=0.8×2w=1.6w
答:(1)t=0时,F=0,求斜面倾角θ为30°;
(2)求0.2s内通过导体棒的电荷量q为0.4C;
(3)求0.2S时导体棒所受外力F的功率为1.6w.
点评 此题考查导体棒切割磁感线产生的感应电流,此题的关键是切割磁感线的有效长度,导体棒中的电流为I,则I=$\frac{E}{L×r}$=$\frac{BLV}{L×r}$=$\frac{BV}{r}$=2A,根据沿斜面方向受力平衡可以求出斜面的倾斜角度以及外力F

 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案 质量为m,电量为q的粒子以速度v从A点沿直径AOB方向射入磁场,从C点射出磁场,OC与OB成60°角,圆形磁场半径为R.不计重力,则粒子在磁场中的( )
质量为m,电量为q的粒子以速度v从A点沿直径AOB方向射入磁场,从C点射出磁场,OC与OB成60°角,圆形磁场半径为R.不计重力,则粒子在磁场中的( )| A. | 运动时间为$\frac{2πm}{3qB}$ | B. | 运动时间为$\frac{πm}{3qB}$ | ||
| C. | 运动半径为$\sqrt{3}$R | D. | 运动半径为$\frac{\sqrt{3}}{3}$R |
 将某均匀的长方体锯成如图所示的A、B两块后,放在水平桌面上并排放在一起,现用水平力F垂直于B的左边推B物体,使A、B整体仍保持矩形沿F方向匀速运动,则( )
将某均匀的长方体锯成如图所示的A、B两块后,放在水平桌面上并排放在一起,现用水平力F垂直于B的左边推B物体,使A、B整体仍保持矩形沿F方向匀速运动,则( )| A. | 物体A在水平方向上受三个力的作用,且合力为零 | |
| B. | 物体A在水平方向上受两个力的作用,且合力为零 | |
| C. | B对A的压力等于桌面对A的摩擦力 | |
| D. | B对A的作用力方向与F方向相同 |
 真空中三个同种点电荷固定在一条直线上,如图所示,三个点电荷的电荷量均为4.0×10-12 C,Q1、Q2相距0.1m,Q2、Q3相距0.2m,求Q1所受的静电力的大小和方向.
真空中三个同种点电荷固定在一条直线上,如图所示,三个点电荷的电荷量均为4.0×10-12 C,Q1、Q2相距0.1m,Q2、Q3相距0.2m,求Q1所受的静电力的大小和方向. 如图所示,有一根长L1=0.5m的木棍,悬挂在某房顶上,木棍的上端与窗台上沿的竖直距离h=4.55m,窗口高为L2=1.5m.某时刻木棍脱落,不计空气阻力,g取10m/s2.求:
如图所示,有一根长L1=0.5m的木棍,悬挂在某房顶上,木棍的上端与窗台上沿的竖直距离h=4.55m,窗口高为L2=1.5m.某时刻木棍脱落,不计空气阻力,g取10m/s2.求: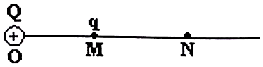 在真空中的0点放一点电荷Q=l.0×10 -9C,直线MN过O点,OM=30cm,M点放有一点电荷q=-2.0×10 -9C,如图所示.求:
在真空中的0点放一点电荷Q=l.0×10 -9C,直线MN过O点,OM=30cm,M点放有一点电荷q=-2.0×10 -9C,如图所示.求: 如图所示,滑块A和B用轻细绳连接在一起后放在水平桌面上,水平恒力F作用在B上,使A,B一起由静止开始沿水平桌面滑动.已知滑块A、B与水平桌面件的动摩擦因数为μ,力F作用时间t后,A,B件连线断开,此后力F仍作用于B,试求:滑块A刚刚停住时,滑块B的速度为多大?设滑块A,B的质量分别为mA,mB.
如图所示,滑块A和B用轻细绳连接在一起后放在水平桌面上,水平恒力F作用在B上,使A,B一起由静止开始沿水平桌面滑动.已知滑块A、B与水平桌面件的动摩擦因数为μ,力F作用时间t后,A,B件连线断开,此后力F仍作用于B,试求:滑块A刚刚停住时,滑块B的速度为多大?设滑块A,B的质量分别为mA,mB.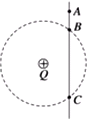 如图所示,光滑绝缘细杆竖直放置,它与以正电荷Q为圆心的某圆交于B、C两点,质量为m、带电荷量-q的有孔小球从杆上A点无初速度下滑,已知q?Q,AB=h,小球滑到B点时的速度大小为$\sqrt{7gh}$.求:
如图所示,光滑绝缘细杆竖直放置,它与以正电荷Q为圆心的某圆交于B、C两点,质量为m、带电荷量-q的有孔小球从杆上A点无初速度下滑,已知q?Q,AB=h,小球滑到B点时的速度大小为$\sqrt{7gh}$.求: 如图所示,竖直光滑杆上套有一个小球和两根弹簧,两弹簧的一端各与小球相连,另一端分别用销钉M、N固定于杆上,小球处于静止状态.设拔去销钉N瞬间,小球加速度的大小为12m/s2.若不拔去销钉N而拔去M销钉瞬间,小球的加速度可能是?(取g=10m/s2)
如图所示,竖直光滑杆上套有一个小球和两根弹簧,两弹簧的一端各与小球相连,另一端分别用销钉M、N固定于杆上,小球处于静止状态.设拔去销钉N瞬间,小球加速度的大小为12m/s2.若不拔去销钉N而拔去M销钉瞬间,小球的加速度可能是?(取g=10m/s2)