题目内容
20. 如图所示,A、B、C三个物体放在旋转圆台上,它们与圆台之间的动摩擦因数均为μ,A的质量为2m,B、C质量均为m,A、B离轴心距离为R,C离轴心2R,则当圆台旋转时(设A、B、C都没有滑动)( )
如图所示,A、B、C三个物体放在旋转圆台上,它们与圆台之间的动摩擦因数均为μ,A的质量为2m,B、C质量均为m,A、B离轴心距离为R,C离轴心2R,则当圆台旋转时(设A、B、C都没有滑动)( )| A. | 物体A的向心加速度最大 | B. | 物体B受到的静摩擦力最大 | ||
| C. | ω=$\sqrt{\frac{μg}{2R}}$是C开始滑动的临界角速度 | D. | 当圆台转速增加时,B比A先滑动 |
分析 抓住A、B、C的角速度相等,结合向心加速度公式比较向心加速度的大小,A、B、C做圆周运动,靠静摩擦力提供向心力,根据牛顿第二定律比较静摩擦力的大小.抓住最大静摩擦力提供向心力求出发生相对滑动的临界角速度,从而确定谁先滑动.
解答 解:A、A、B、C的角速度相等,根据a=rω2知,C的半径最大,则C的向心加速度最大,故A错误.
B、对A,${f}_{A}=2m•R{ω}^{2}$,对B,${f}_{B}=mR{ω}^{2}$,对C,${f}_{C}=m•2R{ω}^{2}=2mR{ω}^{2}$,可知A、C的静摩擦力最大,B受到的静摩擦力最小,故B错误.
C、根据μmg=m•2Rω2得,C发生相对滑动的临界角速度$ω=\sqrt{\frac{μg}{2R}}$,故C正确.
D、根据μmg=mrω2得,$ω=\sqrt{\frac{μg}{r}}$,A、B的半径相等,当圆台转速增加时,A、B同时滑动,故D错误.
故选:C.
点评 解决本题的关键知道物体做圆周运动向心力的来源,抓住临界状态,结合牛顿第二定律进行求解,难度不大.

练习册系列答案
相关题目
10.如图a,物体在水平恒力F作用下沿粗糙水平地面由静止开始运动,在t=1s时刻撤去恒力F.物体运动的v-t图象如图b.重力加速度g=10m/s2,则( )
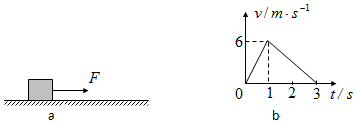
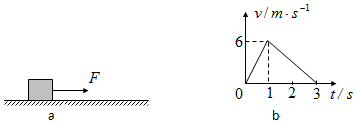
| A. | 物体在3s内的位移s=3m | |
| B. | 恒力F与摩擦力f大小之比F:f=3:1 | |
| C. | 物体与地面的动摩擦因数为μ=0.3 | |
| D. | 3s内恒力做功WF与克服摩擦力做功Wf之比WF:Wf=3:2 |
11. 如图,x轴在水平地面内,y轴沿竖直方向.图中画出了从y轴上沿x轴正向抛出的三个小球a、b和c的运动轨迹,其中b和c是从同一点抛出的,不计空气阻力,则( )
如图,x轴在水平地面内,y轴沿竖直方向.图中画出了从y轴上沿x轴正向抛出的三个小球a、b和c的运动轨迹,其中b和c是从同一点抛出的,不计空气阻力,则( )
 如图,x轴在水平地面内,y轴沿竖直方向.图中画出了从y轴上沿x轴正向抛出的三个小球a、b和c的运动轨迹,其中b和c是从同一点抛出的,不计空气阻力,则( )
如图,x轴在水平地面内,y轴沿竖直方向.图中画出了从y轴上沿x轴正向抛出的三个小球a、b和c的运动轨迹,其中b和c是从同一点抛出的,不计空气阻力,则( )| A. | a的飞行时间比b的短 | B. | b和c的飞行时间相同 | ||
| C. | a的水平速度比b的小 | D. | b的初速度比c的大 |
8.匀加速直线运动的物体的加速度为3m/s2,下列说法正确的是( )
| A. | 任意一秒末的速度总比前一秒初的速度大3m/s | |
| B. | 任意一秒初的速度总比前一秒末的速度大3m/s | |
| C. | 任意一秒的平均速度总比前一秒的平均速度大3m/s | |
| D. | 任意一秒内发生的位移总比前一秒发生的位移大3m |
15. 如图,在同一铁心上绕着两个线圈,单刀双掷开关原来接在1位置,现在它从1打向2位置,试判断此过程中,通过R的电流方向是( )
如图,在同一铁心上绕着两个线圈,单刀双掷开关原来接在1位置,现在它从1打向2位置,试判断此过程中,通过R的电流方向是( )
 如图,在同一铁心上绕着两个线圈,单刀双掷开关原来接在1位置,现在它从1打向2位置,试判断此过程中,通过R的电流方向是( )
如图,在同一铁心上绕着两个线圈,单刀双掷开关原来接在1位置,现在它从1打向2位置,试判断此过程中,通过R的电流方向是( )| A. | 始终是由Q到P | B. | 始终是由P到Q | ||
| C. | 先由P到Q,再由Q到P | D. | 先由Q到P,再由P到Q |
12.一弹簧枪可射出速度为10m/s的铅弹,现对准以6m/s的速度沿光滑桌面迎面滑来的软木块发射一颗铅弹,铅弹射入木块后未穿出,木块继续向前运动,但速度变为5m/s.如果想让木块停止运动,并且铅弹射入木块后都不会穿出,则再向木块迎面射入的铅弹数应为( )
| A. | 5颗 | B. | 6颗 | C. | 7颗 | D. | 8颗 |
15.把力F分解为两个不为零的分力,下列分解哪种是不可能的( )
| A. | 分力之一垂直于F | |
| B. | 两分力都跟F垂直 | |
| C. | 两分力都比F大 | |
| D. | 两分力在同一直线上,并与F方向相同 |