题目内容
5.如图甲所示,一轻弹簧的下端固定在倾角为30°的足够长光滑斜面的底端,上端放一小滑块,滑块与弹簧不拴接.沿斜面向下压滑块至离斜面底端l=0.1m处后由静止释放,滑块的动能Ek与距斜面底端的距离l的关系如图乙所示.其中从0.2m到0.35m范围内图象为直线,其余部分为曲线,不计空气阻力,取g=10m/s2,下列说法正确的是( )
| A. | 小滑块的质量为0.4kg | B. | 弹簧的最大形变量为0.2m | ||
| C. | 弹簧最大弹性势能为0.6J | D. | 弹簧的劲度系数为100N/m |
分析 物体离开弹簧后向上做匀减速运动,只有重力做功,动能转化为重力势能,结合动能定理(机械能守恒)即可求出滑块的质量;由图即可求出弹簧的最大形变量;结合功能关系即可求出弹簧最大弹性势能;
解答 解:A、物体离开弹簧后只有重力做功,动能转化为重力势能,结合动能定理得:-mgsinθ•△l1=△Ek,l1=0.35m-0.20m=0.15m
代入数据得:m=0.4kg.故A正确;
B、由图可知,在弹簧长度是0.2m处滑块与弹簧分离,所以弹簧的原长是0.2m,弹簧的最大形变量为0.2m-0.1m=0.1m.故B错误;
C、滑块释放后到滑块到达最高点时,弹簧的弹性势能转化为滑块的动能,所以:
EPm=-mgsinθ•△l2,l2=0.35m-0.10m=0.25m
与A中的两个公式联立可得:EPm=0.5J.故C错误.
D、根据弹簧的弹性势能的表达式:${E}_{P}=\frac{1}{2}k△{x}^{2}$
可得:$k=\frac{2{E}_{Pm}}{△{x}^{2}}=\frac{2×0.5}{(0.2-0.1)^{2}}=100$N/m.故D正确.
故选:AD
点评 本题结合图象考查动能定理与功能关系的综合应用,综合性较强,通过动能定理得出物体的质量是解决本题的关键.

练习册系列答案
相关题目
13.下列说法正确的是 ( )
| A. | 发现中子的核反应方程是${\;}_{4}^{9}$Be+${\;}_{2}^{4}$He→${\;}_{6}^{12}$C+${\;}_{0}^{1}$ | |
| B. | 结合能越大,原子核结构一定越稳定 | |
| C. | 如果使用某种频率的光不能使某金属发生光电效应,则需增大入射光的光照强度才行 | |
| D. | 发生β衰变时,元素原子核的质量数不变,电荷数增加1 | |
| E. | 在相同速率情况下,利用质子流比利用电子流制造的显微镜将有更高的分辨率 |
10. 表为如图所示“风光互补路灯”中风力发电机部分的配置参数.已知风轮机叶片旋转所扫过的面积为风力发电机可接受风能的面积,风力发电机的输出功率与单位时间内流向风轮机的最大风能P风成正比.则当风垂直通过叶片旋转扫过的平面且风速为6m/s时(忽略空气密度的变化),风力发电机的输出功率为( )
表为如图所示“风光互补路灯”中风力发电机部分的配置参数.已知风轮机叶片旋转所扫过的面积为风力发电机可接受风能的面积,风力发电机的输出功率与单位时间内流向风轮机的最大风能P风成正比.则当风垂直通过叶片旋转扫过的平面且风速为6m/s时(忽略空气密度的变化),风力发电机的输出功率为( )
 表为如图所示“风光互补路灯”中风力发电机部分的配置参数.已知风轮机叶片旋转所扫过的面积为风力发电机可接受风能的面积,风力发电机的输出功率与单位时间内流向风轮机的最大风能P风成正比.则当风垂直通过叶片旋转扫过的平面且风速为6m/s时(忽略空气密度的变化),风力发电机的输出功率为( )
表为如图所示“风光互补路灯”中风力发电机部分的配置参数.已知风轮机叶片旋转所扫过的面积为风力发电机可接受风能的面积,风力发电机的输出功率与单位时间内流向风轮机的最大风能P风成正比.则当风垂直通过叶片旋转扫过的平面且风速为6m/s时(忽略空气密度的变化),风力发电机的输出功率为( )| 最小启动风速 | 1.0m/s |
| 最小充电风速 | 2.0m/s |
| 最大限制风速 | 12.0m/s |
| 最大输出功率 | 400W |
| A. | 25 W | B. | 50 W | C. | 100 W | D. | 200 W |
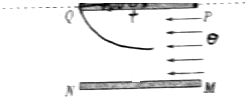 MN、PQ是长为d,间距为d的两块平行金属板,PQ板带正电,MN板带负电,在PQ板所处水平线上方足够大空间内有垂直纸面的匀强磁场,如图所示,一束粒子以相同的速度v0平行两极板射入电场,其中沿两板中线射入的粒子恰好能从PQ板左边缘射入磁场,然后又恰好从PQ板的右边缘射出磁场,已知粒子电荷量为q、质量为m,不计粒子重力、忽略电场的边缘效应,磁感应强度大小B=$\frac{2m{v}_{0}}{qd}$.
MN、PQ是长为d,间距为d的两块平行金属板,PQ板带正电,MN板带负电,在PQ板所处水平线上方足够大空间内有垂直纸面的匀强磁场,如图所示,一束粒子以相同的速度v0平行两极板射入电场,其中沿两板中线射入的粒子恰好能从PQ板左边缘射入磁场,然后又恰好从PQ板的右边缘射出磁场,已知粒子电荷量为q、质量为m,不计粒子重力、忽略电场的边缘效应,磁感应强度大小B=$\frac{2m{v}_{0}}{qd}$. 如图是一个多用表欧姆挡内部电路示意图.电流表满偏电流0.5mA、内阻10Ω;电池电动势1.5V、内阻1Ω;变阻器R0阻值0-5000Ω.
如图是一个多用表欧姆挡内部电路示意图.电流表满偏电流0.5mA、内阻10Ω;电池电动势1.5V、内阻1Ω;变阻器R0阻值0-5000Ω. 如图甲所示,在该磁场外部,有匝数为n、电阻为r、横截面积为S的螺线管和阻值为2r的电阻组成串联电路,螺线管内沿轴线方向存在按如图乙所示变化的磁场,磁场在t0时间内从零开始增大到B0.(to足够长),如图丙所示,两个共轴的正方形金属筒,外极板每边的中点各有一小孔,分别为a、b、c、d,正方形外筒的边长为L,内筒、外筒间距离为d0.在极板外面存在足够大且垂直截面向里的匀强磁场.两个共轴的正方形金属板与与螺线管用导线相连.在t=0时刻,从紧靠内筒且正对狭缝a的S点从静止释放一质量为m、带电量为+q的粒子,该粒子经过一段时间的运动之后恰好又回到出发点S,(不计重力,整个装置在真空中.)
如图甲所示,在该磁场外部,有匝数为n、电阻为r、横截面积为S的螺线管和阻值为2r的电阻组成串联电路,螺线管内沿轴线方向存在按如图乙所示变化的磁场,磁场在t0时间内从零开始增大到B0.(to足够长),如图丙所示,两个共轴的正方形金属筒,外极板每边的中点各有一小孔,分别为a、b、c、d,正方形外筒的边长为L,内筒、外筒间距离为d0.在极板外面存在足够大且垂直截面向里的匀强磁场.两个共轴的正方形金属板与与螺线管用导线相连.在t=0时刻,从紧靠内筒且正对狭缝a的S点从静止释放一质量为m、带电量为+q的粒子,该粒子经过一段时间的运动之后恰好又回到出发点S,(不计重力,整个装置在真空中.)
 如图所示,直角三角形ABC是一玻璃砖的横截面,AB=L,∠C=90°,∠A=60°.一束单色光PD从AB边上的D点射入玻璃砖,入射角为45°,DB=$\frac{L}{4}$,折射光DE恰好射到玻璃砖BC边的中点E,已知光在真空中的传播速度为C.求:
如图所示,直角三角形ABC是一玻璃砖的横截面,AB=L,∠C=90°,∠A=60°.一束单色光PD从AB边上的D点射入玻璃砖,入射角为45°,DB=$\frac{L}{4}$,折射光DE恰好射到玻璃砖BC边的中点E,已知光在真空中的传播速度为C.求: