题目内容
18.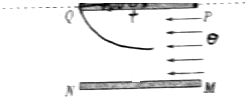 MN、PQ是长为d,间距为d的两块平行金属板,PQ板带正电,MN板带负电,在PQ板所处水平线上方足够大空间内有垂直纸面的匀强磁场,如图所示,一束粒子以相同的速度v0平行两极板射入电场,其中沿两板中线射入的粒子恰好能从PQ板左边缘射入磁场,然后又恰好从PQ板的右边缘射出磁场,已知粒子电荷量为q、质量为m,不计粒子重力、忽略电场的边缘效应,磁感应强度大小B=$\frac{2m{v}_{0}}{qd}$.
MN、PQ是长为d,间距为d的两块平行金属板,PQ板带正电,MN板带负电,在PQ板所处水平线上方足够大空间内有垂直纸面的匀强磁场,如图所示,一束粒子以相同的速度v0平行两极板射入电场,其中沿两板中线射入的粒子恰好能从PQ板左边缘射入磁场,然后又恰好从PQ板的右边缘射出磁场,已知粒子电荷量为q、质量为m,不计粒子重力、忽略电场的边缘效应,磁感应强度大小B=$\frac{2m{v}_{0}}{qd}$.(1)判断磁感应强度的方向;
(2)求两金属板间电压U的大小;
(3)若匀强磁场中距Q点左边的水平距离x=$\frac{2\sqrt{2}-1}{4}$d处有一竖直挡板,打在挡板上的粒子能被吸收,求粒子打在PQ板上表面的范围.
分析 (1)根据粒子在电场中偏转的方向,判断出粒子的电性,然后结合粒子在磁场中偏转的方向,由左手定则即可判断出磁场的方向;
(2)带电粒子在平行金属板间做的是类平抛运动,对物体受力分析,根据平抛运动的规律可以求得电压的大小;
(3)根据粒子在电场中做平抛运动的特点,求出能够射出电场的粒子的范围.以及粒子出射的方向;出电场后,粒子做匀速直线运动,结合运动学的公式求出粒子进入磁场的范围,在根据磁场中运动的规律判断出粒子打在PQ板上表面的范围.
解答 解:(1)根据粒子在电场中向正极偏转的特点,可以判断出粒子带负电;带负电的粒子在磁场中向右偏转,由左手定则可知磁场的方向向里.
(2)设带电粒子在平行金属板匀强电场中运动的时间为t,由类平抛运动可知:
d=v0t ①
$\frac{1}{2}$$d=\frac{1}{2}a{t}^{2}$ ②
$a=\frac{Eq}{m}$ ③
$E=\frac{U}{d}$ ④
由①②③④可解得:
U=$\frac{m{v}_{0}^{2}}{q}$ ⑤
(3)粒子出电场时:vy=at=$\frac{qU}{md}•\frac{d}{{v}_{0}}={v}_{0}$
设速度的偏转角为θ,则:$tanθ=\frac{{v}_{y}}{{v}_{0}}=1$
所以:θ=45°
粒子出电场时的速度:$v=\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}=\sqrt{2}{v}_{0}$ ⑥
带电粒子以速度v飞出电场后射入匀强磁场做匀速圆周运动,粒子在磁场中做圆周运动时洛伦兹力提供向心力有:
$qvB=m\frac{{v}^{2}}{R}$
则粒子运动的半径:$R=\frac{mv}{qB}=\frac{\sqrt{2}m{v}_{0}}{q•\frac{2m{v}_{0}}{qd}}=\frac{\sqrt{2}}{2}d$ ⑦
由类平抛运动的特点可知,射出电场的所有的粒子运动的方向都是相同的,速度的大小也相等,从Q点射入磁场的粒子运动的轨迹如图所示,进入磁场中的粒子若没有打到挡板上,则一定会到达极板PQ的上面,刚好与挡板相切的粒子假设从D点进入磁场,到达PQ上的H点,如图,由图可知,$\overline{PH}=\overline{QD}$,$\overline{PH}$即为粒子打在PQ板上表面的范围.
由几何关系可知,D点到挡板的距离:$x′=R-Rcos45°=R-\frac{\sqrt{2}}{2}R$=$\frac{\sqrt{2}}{2}d(1-\frac{\sqrt{2}}{2})=\frac{2\sqrt{2}-2}{4}d$
所以$\overline{QD}=x-x′=\frac{2\sqrt{2}-1}{4}d-\frac{2\sqrt{2}-2}{4}d$=$\frac{1}{4}d$
则:$\overline{PH}=\frac{1}{4}d$
答:(1)磁感应强度的方向垂直于纸面向里;
(2)两金属板间电压U的大小是$\frac{m{v}_{0}^{2}}{q}$;
(3)若匀强磁场中距Q点左边的水平距离x=$\frac{2\sqrt{2}-1}{4}$d处有一竖直挡板,打在挡板上的粒子能被吸收,粒子打在PQ板上表面的范围是在离P点$\frac{1}{4}$d的范围以内.
点评 本题考查带电粒子在匀强磁场中的运动和带电粒子在电场中的运动,重点是要掌握住半径公式、周期公式.在解答的过程中画出粒子的运动轨迹后,几何关系就比较明显了.

| A. | 气体的内能是所有分子热运动的动能和分子之间势能之和 | |
| B. | 一气球在加速上升的过程中,内部气体分子热运动的动能一定增加 | |
| C. | 液晶的光学性质不随所加电场的变化而变化 | |
| D. | 一定量的气体,在压强不变时,分子每秒对器壁单位面积平均碰撞次数随着温度升高而减小 | |
| E. | 一定量的气体,在温度不变时,分子每秒对器壁单位面积平均碰撞次数随着体积增加而减小 |
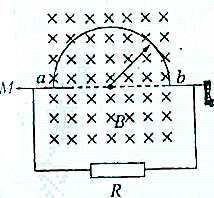 将硬导线中间一段折为半圆形是,使其半径为r(m),让它在磁感应强度为B(T)、方向如图所示的匀强磁场中绕轴MN匀速转动,转速为n(r/s),导线在a、b两处通过电刷与外电路连接,外电路接有阻值为R(Ω)的电阻,其余部分的电阻不计,则( )
将硬导线中间一段折为半圆形是,使其半径为r(m),让它在磁感应强度为B(T)、方向如图所示的匀强磁场中绕轴MN匀速转动,转速为n(r/s),导线在a、b两处通过电刷与外电路连接,外电路接有阻值为R(Ω)的电阻,其余部分的电阻不计,则( )| A. | 通过电阻R的电流恒为$\frac{Bn{π}^{2}{r}^{2}}{R}$ | |
| B. | 电阻R两端的电压的最大值为Bnπ2r2 | |
| C. | 半圆导线从图示位置转过180°的过程中,通过电阻R的电荷量为$\frac{Bπ{r}^{2}}{R}$ | |
| D. | 电阻R上消耗的电功率为$\frac{(Bb{π}^{2}{r}^{2})^{2}}{2R}$ |
 监控系统控制电路如图所示,电键S闭合时,系统白天和晚上都工作;电键S断开时,系统仅晚上工作.在电路中虚框处分别接入光敏电阻(受光照时阻值减小)和定值电阻,则电路中( )
监控系统控制电路如图所示,电键S闭合时,系统白天和晚上都工作;电键S断开时,系统仅晚上工作.在电路中虚框处分别接入光敏电阻(受光照时阻值减小)和定值电阻,则电路中( )| A. | C是“与门”,A是光敏电阻 | B. | C是“与门”,B是光敏电阻 | ||
| C. | C是“或门”,A是光敏电阻 | D. | C是“或门”,B是光敏电阻 |

| A. | 小滑块的质量为0.4kg | B. | 弹簧的最大形变量为0.2m | ||
| C. | 弹簧最大弹性势能为0.6J | D. | 弹簧的劲度系数为100N/m |
 如图所示,光滑圆弧BC与水平面和传送带分别相切于B,C两点,圆弧所对应的圆心角θ=37°,圆弧BC的半径R=7m,足够长的传送带以恒定速率v=4m/s顺时针转动,传送带CD与水平面的夹角也为θ,一质量m=1kg的小滑块从A点以大小v0=10m/s的初速度向B点运动,A,B间的距离s=3.6m,已知小滑块与水平面、传送带之间的动摩擦因数均为μ=0.5,重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.求:
如图所示,光滑圆弧BC与水平面和传送带分别相切于B,C两点,圆弧所对应的圆心角θ=37°,圆弧BC的半径R=7m,足够长的传送带以恒定速率v=4m/s顺时针转动,传送带CD与水平面的夹角也为θ,一质量m=1kg的小滑块从A点以大小v0=10m/s的初速度向B点运动,A,B间的距离s=3.6m,已知小滑块与水平面、传送带之间的动摩擦因数均为μ=0.5,重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.求: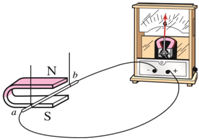 如图所示,是探究“什么情况下磁可以生电”的实验装置:
如图所示,是探究“什么情况下磁可以生电”的实验装置: 如图所示,一质量为m的小球,夹在斜面与竖直挡板之间保持静止,斜面倾角为30°,(不计一切摩擦).求:
如图所示,一质量为m的小球,夹在斜面与竖直挡板之间保持静止,斜面倾角为30°,(不计一切摩擦).求: