题目内容
16. 如图甲所示是研究光电效应规律的电路.用波长λ的光照射光电管的阴极K,实验测得流过G表的电流I与AK之间的电势差UAK满足如图乙所示规律,普朗克常数为h,从图中可得( )
如图甲所示是研究光电效应规律的电路.用波长λ的光照射光电管的阴极K,实验测得流过G表的电流I与AK之间的电势差UAK满足如图乙所示规律,普朗克常数为h,从图中可得( )| A. | 该阴极材料的极限频率为$\frac{{U}_{0}e}{h}$ | |
| B. | 该阴极材料的逸出功为U0e | |
| C. | 光电管每秒钟产生的光电子数为I0e | |
| D. | 光电管产生的光电子的最大初动能为U0e |
分析 根据乙图得出遏止电压的大小,结合动能定理求出光电子的最大初动能.光电子的最大初动能与逸出功不一定相等,根据饱和电流的大小,求出光电管每秒钟产生的光电子数.
解答 解:A、由乙图可知,遏止电压为U0,根据动能定理可知,光电子的最大初动能Ekm=eU0,光电子的最大初动能与逸出功不等,即逸出功不等于eU0,则材料的极限频率${v}_{0}≠\frac{e{U}_{0}}{h}$,故A、B错误,D正确.
C、由图可知,饱和电流为I0,则电流达到饱和时,光电管每秒产生的光电子数n=$\frac{{I}_{0}t}{e}=\frac{{I}_{0}}{e}$,故C错误.
故选:D.
点评 解决本题的关键理解遏止电压的含义,掌握光电效应方程以及电流的定义式,并能灵活运用.

练习册系列答案
相关题目
19.在物理学研究过程中科学家们创造了许多物理学研究方法,如理想实验法、控制变量法、极限法、等效替代法、理想模型法、微元法等,以下关于所用物理学研究方法的叙述错误的是( )
| A. | 根据速度定义式v=$\frac{△x}{△t}$,当△t非常小时,$\frac{△x}{△t}$就可以表示物体在t时刻的瞬时速度,该定义采用了极限法 | |
| B. | 在不需要考虑物体的大小和形状时,用质点来代替实际物体采用了等效替代的方法 | |
| C. | 加速度的定义式为a=$\frac{△v}{△t}$,采用的是比值定义法 | |
| D. | 在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加,这里采用了微元法 |
7.质量为m的物体在水平面上,只受摩擦力作用,以初动能E0做匀变速直线运动,经距离d后,动能减为$\frac{{E}_{0}}{3}$,则( )
| A. | 物体与水平面间的动摩擦因数为$\frac{2{E}_{0}}{3mgd}$ | |
| B. | 物体再前进$\frac{d}{3}$便停止 | |
| C. | 物体滑行距离d所用时间是滑行后面距离所用时间的$\sqrt{3}$倍 | |
| D. | 若要使此物体滑行的总距离为3d,其初动能应为2E0 |
4.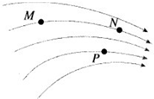 如图为某一电场的电场线,M、N、P为电场线上的三个点,M、N是同一电场线上两点.下列判断正确的是( )
如图为某一电场的电场线,M、N、P为电场线上的三个点,M、N是同一电场线上两点.下列判断正确的是( )
 如图为某一电场的电场线,M、N、P为电场线上的三个点,M、N是同一电场线上两点.下列判断正确的是( )
如图为某一电场的电场线,M、N、P为电场线上的三个点,M、N是同一电场线上两点.下列判断正确的是( )| A. | M、N、P三点中M点的场强最大 | |
| B. | M、N、P三点中N点的电势最高 | |
| C. | 负电荷在M点的电势能小于在N点的电势能 | |
| D. | 正电荷从M点自由释放,电荷将沿电场线运动到N点 |
11. 足球比赛中踢点球时,足球距球门14.00m,球正对球门踢出后恰好沿水平方向从横梁的下沿擦进球门,已知球门高度约2.45m,足球质量约400g,不计空气阻力,则该球员此次踢球过程中对足球做的功约为(g取10m/s2)( )
足球比赛中踢点球时,足球距球门14.00m,球正对球门踢出后恰好沿水平方向从横梁的下沿擦进球门,已知球门高度约2.45m,足球质量约400g,不计空气阻力,则该球员此次踢球过程中对足球做的功约为(g取10m/s2)( )
 足球比赛中踢点球时,足球距球门14.00m,球正对球门踢出后恰好沿水平方向从横梁的下沿擦进球门,已知球门高度约2.45m,足球质量约400g,不计空气阻力,则该球员此次踢球过程中对足球做的功约为(g取10m/s2)( )
足球比赛中踢点球时,足球距球门14.00m,球正对球门踢出后恰好沿水平方向从横梁的下沿擦进球门,已知球门高度约2.45m,足球质量约400g,不计空气阻力,则该球员此次踢球过程中对足球做的功约为(g取10m/s2)( )| A. | 30 J | B. | 60 J | C. | 90 J | D. | 120 J |
8. 如图所示,质量为m的物块放在地面上,在力F的作用下保持静止.经过时间t,重力的冲量是( )
如图所示,质量为m的物块放在地面上,在力F的作用下保持静止.经过时间t,重力的冲量是( )
 如图所示,质量为m的物块放在地面上,在力F的作用下保持静止.经过时间t,重力的冲量是( )
如图所示,质量为m的物块放在地面上,在力F的作用下保持静止.经过时间t,重力的冲量是( )| A. | mgt | B. | Ft | C. | (mg+F)t | D. | 0 |
5.某人将质量为1kg的物体由静止竖直向上提起1m时,物体的速度为2m/s,g取10m/s2,则( )
| A. | 合外力做功12J | B. | 合外力做功2J | ||
| C. | 手对物体的拉力做功12J | D. | 物体克服重力做功12J |
 如图所示,光滑水平AB与竖直面内的半圆形导轨在B点相切,半圆形导轨的半径为R.一个质量为m的物体获得某一向右的速度,当它经过B点进入导轨的瞬间对轨道的压力为其重力的8倍,之后向上运动恰能到达最高点C,已知C、O、B三点在同一竖直线上.不计空气阻力.试求:
如图所示,光滑水平AB与竖直面内的半圆形导轨在B点相切,半圆形导轨的半径为R.一个质量为m的物体获得某一向右的速度,当它经过B点进入导轨的瞬间对轨道的压力为其重力的8倍,之后向上运动恰能到达最高点C,已知C、O、B三点在同一竖直线上.不计空气阻力.试求: 一质量为m=40kg的小孩子站在电梯内的体重计上,电梯从t=0时刻由静止始上升,在0到6s内体重计示数F的变化如图.(取重力加速度g=10m/s2)试问:
一质量为m=40kg的小孩子站在电梯内的体重计上,电梯从t=0时刻由静止始上升,在0到6s内体重计示数F的变化如图.(取重力加速度g=10m/s2)试问: