题目内容
14. 质量为m的物块,沿着半径为R的半球形金属壳内壁滑下,半球形金属壳竖直固定放置,开口向上,滑到最低点时速度大小为v0,则物体在最低点时对金属壳的压力为mg+$\frac{mv_0^2}{R}$.
质量为m的物块,沿着半径为R的半球形金属壳内壁滑下,半球形金属壳竖直固定放置,开口向上,滑到最低点时速度大小为v0,则物体在最低点时对金属壳的压力为mg+$\frac{mv_0^2}{R}$.
分析 物体滑到半球形金属球壳最低点时,由重力和支持力提供向心力.根据牛顿第二定律求出支持力即可.
解答 解:根据牛顿第二定律得知,物体在最低点时的向心力Fn=N-mg=m$\frac{m{v}_{0}^{2}}{R}$
解得:N=mg+$\frac{mv_0^2}{R}$,根据牛顿第三定律可知,物体在最低点时对金属壳的压力为mg+$\frac{mv_0^2}{R}$.
故答案为:mg+$\frac{mv_0^2}{R}$
点评 本题是变速圆周运动动力学问题,关键是分析小球的受力情况,确定向心力的来源.难度不大,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.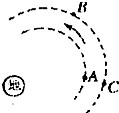 三颗人造地球卫星A、B、C在地球的大气层沿如图所示的方向做匀速圆周运动,已知mA=mB<mC,则三颗卫星( )
三颗人造地球卫星A、B、C在地球的大气层沿如图所示的方向做匀速圆周运动,已知mA=mB<mC,则三颗卫星( )
 三颗人造地球卫星A、B、C在地球的大气层沿如图所示的方向做匀速圆周运动,已知mA=mB<mC,则三颗卫星( )
三颗人造地球卫星A、B、C在地球的大气层沿如图所示的方向做匀速圆周运动,已知mA=mB<mC,则三颗卫星( )| A. | 线速度大小的关系是VA<VB=VC | |
| B. | 周期关系是TA>TB=TC | |
| C. | 向心力大小的关系是FA=FB<FC | |
| D. | 轨道半径和周期的关系是$\frac{{{R}_{A}}^{3}}{{{T}_{A}}^{2}}$=$\frac{{{R}_{B}}^{3}}{{{T}_{B}}^{2}}$=$\frac{{{R}_{C}}^{3}}{{{T}_{C}}^{2}}$ |
19.质点做匀速圆周运动时,下列说法正确的是( )
| A. | 速度的大小和方向都改变 | |
| B. | 匀速圆周运动是匀变速曲线运动 | |
| C. | 当物体做匀速圆周运动时,向心力就是所受合外力,所受合外力就是向心力 | |
| D. | 向心加速度大小不变,方向时刻改变 |
6. 如图,面积为0.1平方米的120匝矩形线圈放在与线圈垂直的匀强磁场中,线圈总电阻1.2欧姆,磁场变化如图,求:
如图,面积为0.1平方米的120匝矩形线圈放在与线圈垂直的匀强磁场中,线圈总电阻1.2欧姆,磁场变化如图,求:
(1)在0.3s内穿过线圈的磁通量的变化量;
(2)0.3s内通过线圈导线横截面的电量.
 如图,面积为0.1平方米的120匝矩形线圈放在与线圈垂直的匀强磁场中,线圈总电阻1.2欧姆,磁场变化如图,求:
如图,面积为0.1平方米的120匝矩形线圈放在与线圈垂直的匀强磁场中,线圈总电阻1.2欧姆,磁场变化如图,求:(1)在0.3s内穿过线圈的磁通量的变化量;
(2)0.3s内通过线圈导线横截面的电量.
14. 如图所示,a、b、c是地球的3颗卫星,轨道均为圆形,其中b、c为地球同步卫星.下列说法正确的是( )
如图所示,a、b、c是地球的3颗卫星,轨道均为圆形,其中b、c为地球同步卫星.下列说法正确的是( )
 如图所示,a、b、c是地球的3颗卫星,轨道均为圆形,其中b、c为地球同步卫星.下列说法正确的是( )
如图所示,a、b、c是地球的3颗卫星,轨道均为圆形,其中b、c为地球同步卫星.下列说法正确的是( )| A. | b、c的线速度大小相等,且大于7.9km/s | |
| B. | a的向心加速度最大,周期也最大 | |
| C. | b、c的轨道一定位于赤道平面 | |
| D. | a卫星由于阻力,轨道半径缓慢减小,其线速度将增大,机械能不变 |



