题目内容
15.已知某半径为R的质量分布均匀的天体,测得它的一个卫星的圆轨道的半径为r,卫星运行的周期为T.假设在该天体表面高度h处以初速度v0沿水平方向抛出一个物体,不计阻力,则水平位移为( )| A. | $\frac{{{v_0}TR}}{2π}\sqrt{\frac{2h}{{{{(r-R)}^3}}}}$ | B. | $\frac{{{v_0}TR}}{2π}\sqrt{\frac{h}{{{{(r-R)}^3}}}}$ | C. | $\frac{{{v_0}TR}}{2π}\sqrt{\frac{2h}{r^3}}$ | D. | $\frac{{{v_0}TR}}{2π}\sqrt{\frac{h}{r^3}}$ |
分析 根据万有引力提供向心力以及万有引力等于重力求出天体表面的重力加速度,根据高度求出平抛运动的时间,结合初速度和时间求出水平位移.
解答 解:根据万有引力提供向心力$G\frac{Mm}{{r}^{2}}=mr\frac{4{π}^{2}}{{T}^{2}}$得:$GM=\frac{4{π}^{2}{r}^{3}}{{T}^{2}}$,
根据$G\frac{Mm}{{R}^{2}}=mg$得天体表面的重力加速度为:g=$\frac{GM}{{R}^{2}}$=$\frac{4{π}^{2}{r}^{3}}{{R}^{2}{T}^{2}}$,
根据h=$\frac{1}{2}g{t}^{2}$得:t=$\sqrt{\frac{2h}{g}}$,则水平位移为:x=v0t=${v}_{0}\sqrt{\frac{2h}{g}}$=$\frac{{v}_{0}TR}{2π}\sqrt{\frac{2h}{{r}^{3}}}$.
故选:C.
点评 本题考查了平抛运动和万有引力定律的综合运用,掌握万有引力定律的两个重要理论:1、万有引力提供向心力,2、万有引力等于重力,并能灵活运用.

练习册系列答案
相关题目
1.以下说法正确的是( )
| A. | 物体速度越小,加速度一定越小 | |
| B. | 物体在某时刻速度为零,其加速度也一定为零 | |
| C. | 只要物体有加速度,其速度一定是越来越大 | |
| D. | 物体速度变化越慢,加速度一定越小 |
6. 如图所示,一轻绳绕过定滑轮,左右两端分别系有物块甲、乙,不计滑轮的摩擦,重力加速度为g.让物块由静止开始释放后,下列说法正确的是( )
如图所示,一轻绳绕过定滑轮,左右两端分别系有物块甲、乙,不计滑轮的摩擦,重力加速度为g.让物块由静止开始释放后,下列说法正确的是( )
 如图所示,一轻绳绕过定滑轮,左右两端分别系有物块甲、乙,不计滑轮的摩擦,重力加速度为g.让物块由静止开始释放后,下列说法正确的是( )
如图所示,一轻绳绕过定滑轮,左右两端分别系有物块甲、乙,不计滑轮的摩擦,重力加速度为g.让物块由静止开始释放后,下列说法正确的是( )| A. | 若甲、乙的质量均为m,则轻绳中的拉力大小为2mg | |
| B. | 若甲、乙的质量分别为m、2m,则轻绳中的拉力大小为3mg | |
| C. | 若甲、乙的质量分别为m、2m.则经绳中的拉力大于mg | |
| D. | 若甲、乙的质量分别为m、2m,则轻绳中的拉力小于2mg |
3. 如图物体A叠放在物体B上,B置于光滑水平面上.A,B质量分别为mA=4kg,mB=2kg,A,B之间的动摩擦因数μ=0.2,一水平向右的力F作用在A上,开始时F=10N,此后逐渐增加,在增大到21N的过程中,设最大静摩擦力等于滑动摩擦力,g取10m/s2,则( )
如图物体A叠放在物体B上,B置于光滑水平面上.A,B质量分别为mA=4kg,mB=2kg,A,B之间的动摩擦因数μ=0.2,一水平向右的力F作用在A上,开始时F=10N,此后逐渐增加,在增大到21N的过程中,设最大静摩擦力等于滑动摩擦力,g取10m/s2,则( )
 如图物体A叠放在物体B上,B置于光滑水平面上.A,B质量分别为mA=4kg,mB=2kg,A,B之间的动摩擦因数μ=0.2,一水平向右的力F作用在A上,开始时F=10N,此后逐渐增加,在增大到21N的过程中,设最大静摩擦力等于滑动摩擦力,g取10m/s2,则( )
如图物体A叠放在物体B上,B置于光滑水平面上.A,B质量分别为mA=4kg,mB=2kg,A,B之间的动摩擦因数μ=0.2,一水平向右的力F作用在A上,开始时F=10N,此后逐渐增加,在增大到21N的过程中,设最大静摩擦力等于滑动摩擦力,g取10m/s2,则( )| A. | 当拉力F<12N时,两物体均保持静止状态 | |
| B. | 两物体开始没有相对运动,当拉力超过8N时,开始相对滑动 | |
| C. | 两物体间从受力开始就有相对运动 | |
| D. | 两物体间始终没有相对运动 |
20.下列说法正确的是 ( )
| A. | 全息照相利用了激光方向性好的特点 | |
| B. | 光速不变原理指出光在真空中传播速度在不同惯性参考系中都是相同的 | |
| C. | 电磁波和机械波都能产生多普勒效应 | |
| D. | 门镜可以扩大视野是利用光的衍射现象 | |
| E. | 在光的双缝干涉实验中,条纹间距与缝的宽度无关. |
7.飞机以150m/s的水平速度匀速飞行,某时刻释放A球,相隔1s后又让B球落下,不计空气阻力,在以后的运动中关于A球与B球的相对位置关系,正确的是( )
| A. | A球在B球的前下方 | B. | A球在B球的后下方 | ||
| C. | A球在B球的正下方 | D. | 两球间的距离总是相距150m. |
5.关于动能定理的表达式W=Ek2-Ek1,下列说法正确的是( )
| A. | 公式中的W为不包含重力的其他力做的总功 | |
| B. | 动能定理适用于直线运动,但不适用于曲线运动,适用于恒力做功,但不适用于变力做功 | |
| C. | 公式中的Ek2-Ek1为动能的增量,当W>0时动能增加,当W<0时,动能减少 | |
| D. | 运动物体所受合外力不为零,则该物体一定做变速运动,其动能要变化 |
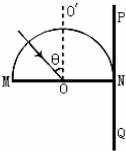 半径为R的固定半圆形玻璃砖的横截面如图所示,O点为圆心,OO′为直径MN的垂线.足够大的光屏PQ紧靠在玻璃砖的右侧且与MN垂直.一束复色光沿半径方向与OO′成θ=30°角射向O点,已知有两束折射率n1=$\sqrt{2}$,n2=$\sqrt{3}$的光束,因而光屏两个光斑.
半径为R的固定半圆形玻璃砖的横截面如图所示,O点为圆心,OO′为直径MN的垂线.足够大的光屏PQ紧靠在玻璃砖的右侧且与MN垂直.一束复色光沿半径方向与OO′成θ=30°角射向O点,已知有两束折射率n1=$\sqrt{2}$,n2=$\sqrt{3}$的光束,因而光屏两个光斑.