题目内容
1.人造地球卫星绕地球做匀速圆周运动,例如卫星的周期增大到原来的8倍,卫星仍做匀速圆周运动,则下列说法中正确的是( )| A. | 卫星的向心加速度增大到原来的4倍 | |
| B. | 卫星的角速度减小到原来的$\frac{1}{4}$ | |
| C. | 卫星的动能将增大到原来的4倍 | |
| D. | 卫星的线速度减小到原来的$\frac{1}{2}$ |
分析 人造地球卫星绕地球做匀速圆周运动,靠地球的万有引力提供向心力,根据牛顿第二定律和万有引力定律得出周期、向心加速度、角速度、线速度与轨道半径的关系,从而判断出它们大小的变化.
解答 解:A、卫星的向心力由地球的万有引力提供,由$G\frac{Mm}{{r}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}r$,得卫星运动的周期T=2πr$\sqrt{\frac{r}{GM}}$,可得卫星的周期增大到原来的8倍,轨道半径增大为原来的4倍.
由$G\frac{Mm}{{r}_{\;}^{2}}$=ma,得a=$\frac{GM}{{r}_{\;}^{2}}$,则知卫星的向心加速度减小到原来的$\frac{1}{16}$,故A错误.
B、由$G\frac{Mm}{{r}_{\;}^{2}}$=mω2r,得ω=$\sqrt{\frac{GM}{{r}_{\;}^{3}}}$,则知卫星的角速度减小到原来的$\frac{1}{8}$,故B错误.
CD、由$G\frac{Mm}{{r}_{\;}^{2}}$=m$\frac{{v}_{\;}^{2}}{r}$,解得:v=$\sqrt{\frac{GM}{r}}$,则知卫星的线速度减小到原来的$\frac{1}{2}$,由${E}_{k}^{\;}=\frac{1}{2}m{v}_{\;}^{2}$知,卫星的动能将减小到原来的$\frac{1}{4}$,故C错误,D正确.
故选:D
点评 解决本题的关键掌握万有引力提供向心力,能灵活选择向心力公式的形式,列式求解比例关系.

练习册系列答案
相关题目
10.质量为m的物体做自由落体运动,经过时间t落地.在物体下落的过程中,以下说法正确的是( )
| A. | 下落过程中,重力的平均功率为$\frac{1}{2}$mg2t | |
| B. | 下落过程中,重力的平均功率为mg2t | |
| C. | 落地前瞬间,重力的瞬时功率为$\frac{1}{2}$mg2t | |
| D. | 落地前瞬间,重力的瞬时功率为mg2t |
12.质量为m的物体,在距地面h高处以$\frac{1}{3}$g的加速度由静止竖直下落到地面,下列说法中正确的有( )
| A. | 物体的重力势能减少mgh | B. | 物体的机械能减少$\frac{2}{3}$mgh | ||
| C. | 物体的动能增加$\frac{1}{3}$mgh | D. | 重力做功$\frac{1}{3}$mgh |
9. 如图甲所示,固定斜面的倾角为30°,斜面足够长,粗糙情况相同,一质量为m的小物块自斜面底端以初速度v0沿斜面向上做匀减速运动,经过一段时间后,又沿斜面下滑回到底端,整个过程小物块的v-t图象如图乙所示.现使该物块从斜面底端以初速度2v0沿斜面向上滑,经一段时间返回出发点,则下列判断正确的是( )
如图甲所示,固定斜面的倾角为30°,斜面足够长,粗糙情况相同,一质量为m的小物块自斜面底端以初速度v0沿斜面向上做匀减速运动,经过一段时间后,又沿斜面下滑回到底端,整个过程小物块的v-t图象如图乙所示.现使该物块从斜面底端以初速度2v0沿斜面向上滑,经一段时间返回出发点,则下列判断正确的是( )
 如图甲所示,固定斜面的倾角为30°,斜面足够长,粗糙情况相同,一质量为m的小物块自斜面底端以初速度v0沿斜面向上做匀减速运动,经过一段时间后,又沿斜面下滑回到底端,整个过程小物块的v-t图象如图乙所示.现使该物块从斜面底端以初速度2v0沿斜面向上滑,经一段时间返回出发点,则下列判断正确的是( )
如图甲所示,固定斜面的倾角为30°,斜面足够长,粗糙情况相同,一质量为m的小物块自斜面底端以初速度v0沿斜面向上做匀减速运动,经过一段时间后,又沿斜面下滑回到底端,整个过程小物块的v-t图象如图乙所示.现使该物块从斜面底端以初速度2v0沿斜面向上滑,经一段时间返回出发点,则下列判断正确的是( )| A. | 滑块沿斜面上滑的整个过程中机械能减小$\frac{m{{v}_{0}}^{2}}{4}$ | |
| B. | 滑块沿斜面上滑的整个过程中机械能减小$\frac{m{{v}_{0}}^{2}}{2}$ | |
| C. | 滑块沿斜面下滑的整个过程中动能增加mv02 | |
| D. | 滑块沿斜面下滑的整个过程中动能增加$\frac{m{{v}_{0}}^{2}}{2}$ |
6.如图是物体做直线运动的v-t图象,由图可知,该物体( )


| A. | 第1s内和第3s内的运动方向相反 | B. | 第3s内和第4s内的加速度不相同 | ||
| C. | 第1s内和第4s内的位移大小相等 | D. | 0~2s和0~4s内的平均速度大小相等 |
13.摩天大楼的一部直通高层的电梯,行程超过百米.电梯的简化模型如图1所示,考虑安全、舒适、省时等因素,电梯的加速度a是随时间t而变化的.已知电梯在t=0时由静止开始上升,a-t图如图2所示.电梯总质量m=2.0×103kg,忽略一切阻力,重力加速度g取l0m/s2.则下列说法中正确的是( )


| A. | 电梯在上升过程中受到的最大拉力F1和最小拉力F2之比为11:9 | |
| B. | 类比是一种常用的研究方法,对于直线运动,教科书中讲解由v-t图象求位移的方法.请你借鉴此方法,对比加速度和速度的定义,根据图2所示a-I图象,可求出电梯在第2s末的速率v2=1.5m/s | |
| C. | 电梯以最大速率上升时,拉力做功的功率为2.0×105W | |
| D. | 0-11s内拉力和重力对电梯所做的总功为零 |
6.如图甲所示,竖直平面内的光滑轨道由倾斜直轨道AB和圆轨道BCD组成,AB和BCD相切于B点,CD连线是圆轨道竖直方向的直径(C、D为圆轨道的最低点和最高点),已知∠BOC=30°.可视为质点的小滑块从轨道AB上高H处的某点由静止滑下,用力传感器测出小滑块经过圆轨道最高点D时对轨道的压力为F,并得到如图乙所示的压力F与高度H的关系图象,取g=10m/s2.则( )
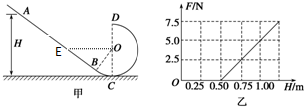

| A. | 圆轨道的半径为0.2m | |
| B. | 无法计算出小滑块的质量 | |
| C. | H取合适的值,可以使得小滑块经过最高点D后直接落到轨道AB上与圆心O等高的E点 | |
| D. | 由图乙可知,若H<0.50m,小滑块一定会在运动到D点之前脱离轨道 |
 如图,PQ⊥MN,其中一个为界面,一个为法线,光线在空气和介质的分界面上同时发生反射和折射的3条光线为a、b、c.由图可知该介质的折射率为n=$\sqrt{2}$,若光在真空中的速度为c,则光在该介质中的速度大小为$\frac{\sqrt{2}}{2}$c.
如图,PQ⊥MN,其中一个为界面,一个为法线,光线在空气和介质的分界面上同时发生反射和折射的3条光线为a、b、c.由图可知该介质的折射率为n=$\sqrt{2}$,若光在真空中的速度为c,则光在该介质中的速度大小为$\frac{\sqrt{2}}{2}$c. 如图所示,细线下面悬挂一钢球(可看作质点),钢球在水平面内以O′为圆心做匀速圆周运动.若测得钢球做圆周运动的轨道半径为r,悬点O到圆心O′之间的距离为h,钢球质量为m.忽略空气阻力,重力加速度为g.求:
如图所示,细线下面悬挂一钢球(可看作质点),钢球在水平面内以O′为圆心做匀速圆周运动.若测得钢球做圆周运动的轨道半径为r,悬点O到圆心O′之间的距离为h,钢球质量为m.忽略空气阻力,重力加速度为g.求: