题目内容
11. 如图所示,在光滑水平面上有一木块A质量为m,靠在竖直墙壁上,用一轻质弹簧与质量为2m的物体B相连,现用力向左推B,使弹簧压缩至弹性势能为E0,然后突然释放,求:
如图所示,在光滑水平面上有一木块A质量为m,靠在竖直墙壁上,用一轻质弹簧与质量为2m的物体B相连,现用力向左推B,使弹簧压缩至弹性势能为E0,然后突然释放,求:(1)木块A脱离墙壁瞬间物体B的速度大小
(2)木块A脱离墙壁后弹簧具有的最大弹性势能
(3)整个过程中木块A所获得的最大速度和最小速度.
分析 (1)当刚离开墙壁时,由机械能守恒求出A物块的速度大小
(2)当弹簧的弹性势能最大时,弹簧达到最大程度时,由动量定理求得共同速度,再由能量守恒定律求解.
(3)A离开墙壁后,弹簧第一次恢复原长时,木块A的速度最大,有能量守恒结合动量定理求解,最小速度为零.
解答 解:(1)当A离开墙壁时,B的速度为v0,由机械能守恒有:$\frac{1}{2}$2mv02=E0
解得:v0=$\sqrt{\frac{{E}_{0}}{m}}$
(2)以后运动中,当弹簧的弹性势能最大时,弹簧达到最大程度时,A、B速度相等,设为v,规定向右为正方向,由动量守恒有:
3mv=2mv0 解得:v=$\frac{2{v}_{0}}{3}$,
有能量守恒定律得:${E}_{P}=\frac{1}{2}2m{v}_{0}^{2}-\frac{1}{2}3m{v}^{2}=\frac{1}{3}m{v}_{0}^{2}$=$\frac{{E}_{0}}{3}$
(3)A离开墙壁后,弹簧第一次恢复原长时,木块A的速度最大,故:
2mv=mvA+2mvB
E0=$\frac{1}{2}$$m{v}_{A}^{2}+\frac{1}{2}m{v}_{B}^{2}$
解得:
vA=$\frac{4}{3}$$\sqrt{\frac{{E}_{0}}{m}}$或vA=0(舍去)
最小速度为零.
答:(1)木块A脱离墙壁瞬间物体B的速度大小$\sqrt{\frac{{E}_{0}}{m}}$
(2)木块A脱离墙壁后弹簧具有的最大弹性势能为$\frac{{E}_{0}}{3}$
(3)整个过程中木块A所获得的最大速度为$\frac{4}{3}$$\sqrt{\frac{{E}_{0}}{m}}$,最小速度为0.
点评 正确认识动量守恒条件和机械能守恒条件是解决本题的关键了.如果一个系统不受外力或所受外力的矢量和为零,那么这个系统的总动量保持不变;系统只有重力或弹力做功为机械能守恒条件.

 如图所示,一个质量为0.4kg的小物块从高h=0.05m的坡面顶端由静止释放,滑到水平台上,滑行一段距离后,从边缘O点水平飞出,击中平台右下侧挡板上的P点,现以O为原点在竖直面内建立如图所示的平面直角坐标系,挡板的形状满足方程y=x2-6(单位:m)不计一切摩擦和空气阻力,g=10m/s2,则下列说法正确的是( )
如图所示,一个质量为0.4kg的小物块从高h=0.05m的坡面顶端由静止释放,滑到水平台上,滑行一段距离后,从边缘O点水平飞出,击中平台右下侧挡板上的P点,现以O为原点在竖直面内建立如图所示的平面直角坐标系,挡板的形状满足方程y=x2-6(单位:m)不计一切摩擦和空气阻力,g=10m/s2,则下列说法正确的是( )| A. | 小物块从水平台上O点飞出的速度大小为1m/s | |
| B. | 小物块从O点运动到P点的时间为1s | |
| C. | 小物块刚到P点时速度方向与水平方向夹角的正切值等于5 | |
| D. | 小物块刚到P点时速度的大小为10m/s |
 如图所示,真空中有一个半径r=0.5m的圆形磁场,与坐标原点相切,磁场的磁感应强度大小B=2.0×10-3T,方向垂直于纸面向里,在x=r处的虚线右侧有一个方向竖直向上的宽度为L1=0.5m的匀强电场区域,电场强度E=1.5×103N/C,在x=2m处有一垂直x方向的足够长的荧光屏,从O点处向不同方向发射出速率相同的荷质比$\frac{q}{m}$=1.0×109C/kg带负电的粒子,粒子的运动轨迹在纸面内.一个速度方向沿y轴正方向射入磁场的粒子甲,恰能从磁场与电场的相切处进入电场.不计重力及阻力的作用.求:
如图所示,真空中有一个半径r=0.5m的圆形磁场,与坐标原点相切,磁场的磁感应强度大小B=2.0×10-3T,方向垂直于纸面向里,在x=r处的虚线右侧有一个方向竖直向上的宽度为L1=0.5m的匀强电场区域,电场强度E=1.5×103N/C,在x=2m处有一垂直x方向的足够长的荧光屏,从O点处向不同方向发射出速率相同的荷质比$\frac{q}{m}$=1.0×109C/kg带负电的粒子,粒子的运动轨迹在纸面内.一个速度方向沿y轴正方向射入磁场的粒子甲,恰能从磁场与电场的相切处进入电场.不计重力及阻力的作用.求:

 如图所示,AB为半径为R的金属导轨,a,b为分别沿导轨上下两表面做圆周运动的小球,要使小球不致脱离导轨,则a,b在导轨最高点的速度va,vb应满足什么条件?
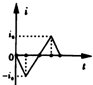
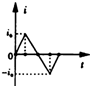
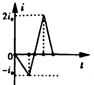
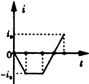
如图所示,AB为半径为R的金属导轨,a,b为分别沿导轨上下两表面做圆周运动的小球,要使小球不致脱离导轨,则a,b在导轨最高点的速度va,vb应满足什么条件?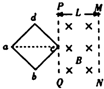 如图所示,宽度为L的匀强磁场的方向垂直纸面向里,正方形线圈abcd的对角线ac与磁场边界PQ垂直,对角线ac的长度也为L,现让正方形线圈abcd以速度v匀速穿过匀强磁场,规定线圈中的电流以顺时针方向为正方向,则在线圈穿过磁场的过程中.电流i随时间t变化的大致情况为( )
如图所示,宽度为L的匀强磁场的方向垂直纸面向里,正方形线圈abcd的对角线ac与磁场边界PQ垂直,对角线ac的长度也为L,现让正方形线圈abcd以速度v匀速穿过匀强磁场,规定线圈中的电流以顺时针方向为正方向,则在线圈穿过磁场的过程中.电流i随时间t变化的大致情况为( )