题目内容
16．物体质量m=5kg，放在动摩擦因数为μ=0.2的水平地面上，受到F=15N的水平力作用静止起移动s1=4m后撤去F，再移动s2=1m，求此时物体速度的大小．分析 根据牛顿第二定律求出物体的加速度，通过位移速度公式求出物体的速度；撤去拉力后，通过牛顿第二定律求出加速度的大小，根据速度位移公式求出物体的速度．
解答 解：根据牛顿第二定律得：a1=$\frac{F-μmg}{m}$=$\frac{15-0.2×5×10}{5}$m/s2=1m/s2．
则物体运动的速度为：v1=$\sqrt{2{a}_{1}{s}_{1}}$=$\sqrt{2×1×4}$=$\sqrt{8}$m/s．
撤去F匀减速运动的加速度为：a2=$\frac{μmg}{m}$=μg=2m/s2
则根据速度位移公式知：v=$\sqrt{2{a}_{2}{s}_{2}+{v}_{0}^{2}}$=$\sqrt{-2×2×1+8}$=2m/s．
答：物体速度的大小为2m/s．
点评 本题考查了牛顿第二定律和运动学公式的基本运用，知道加速度是联系力学和运动学的桥梁．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，闭合的单匝线圈放在匀强磁场中，以角速度ω=300rad/s绕中心轴oo′逆时针匀速转动（沿oo′方向看）．oo′轴垂直磁场方向．线圈的ab边长为0.1m，bc边长为0.2m，线圈的总电阻R=0.05Ω，B=0.5T．从中性面开始转动，求：
7．
“嫦娥一号”探月卫星沿地月转移轨道直奔月球，在距月球表面200km的P点进行第一次变轨后被月球捕获，先进入椭圆轨道Ⅰ绕月飞行，如图所示．之后，卫星在P点又经过两次变轨，最后在距月球表面200km的圆形轨道Ⅲ上绕月球做匀速圆周运动．对此，下列说法正确的是（ ）
“嫦娥一号”探月卫星沿地月转移轨道直奔月球，在距月球表面200km的P点进行第一次变轨后被月球捕获，先进入椭圆轨道Ⅰ绕月飞行，如图所示．之后，卫星在P点又经过两次变轨，最后在距月球表面200km的圆形轨道Ⅲ上绕月球做匀速圆周运动．对此，下列说法正确的是（ ）| A． | 卫星在轨道Ⅲ上运动的速度等于月球的第一宇宙速度 | |
| B． | 卫星在轨道Ⅲ上运动周期比在轨道Ⅰ上短 | |
| C． | 卫星在轨道Ⅲ上运动的加速度大于沿轨道Ⅰ运动到P点时的加速度 | |
| D． | Ⅰ、Ⅱ、Ⅲ三种轨道运行相比较，卫星在轨道Ⅲ上运行的机械能最小 |
如图所示，在光滑水平面上有一木块A质量为m，靠在竖直墙壁上，用一轻质弹簧与质量为2m的物体B相连，现用力向左推B，使弹簧压缩至弹性势能为E0，然后突然释放，求：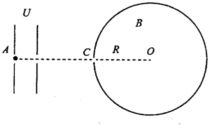
在光滑绝缘的水平面上，左侧平行极板间有水平方向匀强电场，右侧圆筒内有竖直方向匀强磁场，磁感应强度大小为B，俯视图如图所示，圆的圆心为O点，半径大小为R，一质量为m、电荷量大小为q的带电小球（可视为质点），初速位置在A点，现由静止经电场加速后从C孔沿直径射入磁场区域，粒子和圆筒壁的碰撞没有动能和电荷量损失，B、R、m、q为已知量，圆筒仅有一个出入口C．
如图所示，真空中存在空间范围足够大、方向水平向右的匀强磁场，在电场中，一个质量为m、电荷量为q的离子，以大小为V0的初速度从O点以与电场负方向成θ=45°角的方向向上做直线运动．
16．一弹簧振子，当t=0时，物体处在x=-$\frac{A}{2}$（A为振幅）处且向负方向运动，则它的初相为（ ）
| A． | $\frac{π}{3}$ | B． | -$\frac{π}{3}$ | C． | -$\frac{2π}{3}$ | D． | $\frac{2π}{3}$ |