题目内容
9.质量为2×103kg、额定功率为100kw的汽车,在某平直公路上行驶时所受阻力恒定,所能达到的最大速度为20m/s.若汽车从静止开始以2m/s2的加速度作匀加速直线运动,且经25s达到最大速度,求:(1)汽车在该平直公路上行驶时所受的阻力大小;
(2)汽车作匀加速运动的最长时间为多少?
(3)25s内通过的总路程为多少?
分析 这题考的知识点是汽车的两种启动方式,恒定加速度启动和恒定功率启动.本题属于恒定加速度启动方式,由于牵引力不变,根据p=Fv可知随着汽车速度的增加,汽车的实际功率在增加,此过程汽车做匀加速运动,当实际功率达到额定功率时,功率不能增加了,要想增加速度,就必须减小牵引力,当牵引力减小到等于阻力时,加速度等于零,速度达到最大值.
解答 解:(1)当阻力等于牵引力时,汽车达到最大速度为vm=$\frac{P}{f}$,则有:f=$\frac{P}{{v}_{m}}=\frac{100000}{20}$=5000N;
(2)根据牛顿第二定律得:F-f=ma;
解得:F=ma+f=2000×2+5000=9000N
匀加速运动的最大速度为:v=$\frac{P}{F}=\frac{100000}{9000}$=$\frac{100}{9}m/s$
所以匀加速运动的时间:t=$\frac{v}{a}=\frac{100}{18}=5.6s$,
(3)对25s内的过程中,根据动能定理得:
$\frac{1}{2}m{{v}_{m}}^{2}=F•\frac{1}{2}a{t}^{2}+P×(25-t)-fs$,其中t=5.6s
解得:s=364.44m.
答:(1)汽车在该平直公路上行驶时所受的阻力大小wei 5000N;
(2)汽车作匀加速运动的最长时间为5.6s;
(3)25s内通过的总路程为364.44m.
点评 本题考查的是机车启动的两种方式,即恒定加速度启动和恒定功率启动.要求同学们能对两种启动方式进行动态分析,能画出动态过程的方框图,公式p=Fv,p指实际功率,F表示牵引力,v表示瞬时速度.当牵引力等于阻力时,机车达到最大速度.

练习册系列答案
相关题目
12.法国科学家拉普拉斯曾说过:“认识一位巨人的研究方法对于科学的进步并不比发现本身有更少的用处…”.在物理学的重大发现中科学家们创造出了许多物理学方法,如观察、实验、建立模型、物理类比和物理假说等方法.其中物理假说,是根据一定的科学事实和科学理论对研究的问题提出假说性的看法或说明,以下不是属于物理假说的是( )
| A. | 安培分子电流 | B. | 麦克斯韦电磁场理论 | ||
| C. | 爱因斯坦光子说 | D. | 法拉第发现电磁感应现象 |
20. 倾角为θ的斜面上部存在竖直向下的匀强电场.两带电量分别为q1q2质量分别为m1、m2的粒子以速度v1、v2垂直电场射入,并在斜面上某点以速度v1′、v2′射出,在电场中的时间分别为t1、t2.入射速度为v2的粒子射的更远,如图所示,不计粒子重力.下列说法正确的是( )
倾角为θ的斜面上部存在竖直向下的匀强电场.两带电量分别为q1q2质量分别为m1、m2的粒子以速度v1、v2垂直电场射入,并在斜面上某点以速度v1′、v2′射出,在电场中的时间分别为t1、t2.入射速度为v2的粒子射的更远,如图所示,不计粒子重力.下列说法正确的是( )
 倾角为θ的斜面上部存在竖直向下的匀强电场.两带电量分别为q1q2质量分别为m1、m2的粒子以速度v1、v2垂直电场射入,并在斜面上某点以速度v1′、v2′射出,在电场中的时间分别为t1、t2.入射速度为v2的粒子射的更远,如图所示,不计粒子重力.下列说法正确的是( )
倾角为θ的斜面上部存在竖直向下的匀强电场.两带电量分别为q1q2质量分别为m1、m2的粒子以速度v1、v2垂直电场射入,并在斜面上某点以速度v1′、v2′射出,在电场中的时间分别为t1、t2.入射速度为v2的粒子射的更远,如图所示,不计粒子重力.下列说法正确的是( )| A. | 若v1<v2,则t1<t2 | B. | 若v1=v2,则$\frac{{q}_{1}}{{m}_{1}}$>$\frac{{q}_{2}}{{m}_{2}}$ | ||
| C. | 若v1>v2,则v1′<v2′ | D. | 若v1=v2,则v1′=v2′ |
17.同步卫星是指相对于地面不动的人造地球卫星,下列判断正确的是( )
| A. | 它可以静止在地面上任意一点的正上方,离地心的距离可按需要选择不同的值 | |
| B. | 它可以静止在地面上任意一点的正上方,但离地心的距离是一定的 | |
| C. | 它只能静止在赤道的正上方,但离地心的距离可按需要选择不同的值 | |
| D. | 它只能静止在赤道的正上方,且离地心的距离是一定的 |
14. 如图所示,位于介质Ⅰ和Ⅱ分界面上的波源S,产生两列分别沿x轴负方向与正方向传播的机械波.若在两种介质中波的频率及传播速度分别为f1、f2和v1、v2,则( )
如图所示,位于介质Ⅰ和Ⅱ分界面上的波源S,产生两列分别沿x轴负方向与正方向传播的机械波.若在两种介质中波的频率及传播速度分别为f1、f2和v1、v2,则( )
 如图所示,位于介质Ⅰ和Ⅱ分界面上的波源S,产生两列分别沿x轴负方向与正方向传播的机械波.若在两种介质中波的频率及传播速度分别为f1、f2和v1、v2,则( )
如图所示,位于介质Ⅰ和Ⅱ分界面上的波源S,产生两列分别沿x轴负方向与正方向传播的机械波.若在两种介质中波的频率及传播速度分别为f1、f2和v1、v2,则( )| A. | f1=2f2,v1=v2 | B. | f1=f2,v1=2v2 | C. | f1=f2,v1=v2 | D. | f1=f2,v1=0.5v2 |
18.当一个做匀速圆周运动的人造卫星的轨道半径变为原来的2倍时,下列说法正确的是( )
| A. | 卫星的线速度变为原来的$\frac{{\sqrt{2}}}{2}$倍 | B. | 卫星的角速度变为原来的$\frac{{\sqrt{2}}}{2}$倍 | ||
| C. | 卫星所需的向心力变为原来的$\frac{1}{2}$倍 | D. | 卫星的周期变为原来的2$\sqrt{2}$倍 |
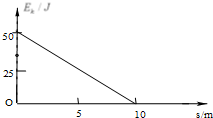 质量为2kg的物体以50J的初动能在粗糙的水平面上滑行,其动能变化与位移的关系如图所示,则物体在水平面上滑行的时间为$2\sqrt{2}$;若该物体以30J的初动能在同一粗糙的水平面上滑行时,其可滑行的最远距离为6m.
质量为2kg的物体以50J的初动能在粗糙的水平面上滑行,其动能变化与位移的关系如图所示,则物体在水平面上滑行的时间为$2\sqrt{2}$;若该物体以30J的初动能在同一粗糙的水平面上滑行时,其可滑行的最远距离为6m. 如图所示是自行车传动部分的结构示意图,牙盘A 通过链条和飞轮B相连,飞轮与后轮C同轴,已知牙盘A、飞轮B和后轮C的半径分别为20cm、10cm、30cm,则当人踩踏脚板使自行车以3m/s的速度在平直的水平路面上匀速前进时,求:
如图所示是自行车传动部分的结构示意图,牙盘A 通过链条和飞轮B相连,飞轮与后轮C同轴,已知牙盘A、飞轮B和后轮C的半径分别为20cm、10cm、30cm,则当人踩踏脚板使自行车以3m/s的速度在平直的水平路面上匀速前进时,求: 倾角为30°的足够长光滑斜面下端与一足够长光滑水平面相接,连接处用一光滑小圆弧过渡,斜面上距水平面高度分别为h1=5m和h2=0.2m的两点上,各固定一小球A和B.某时刻由静止开始释放A球,经过一段时间t后,同样由静止开始释放B球.g取10m/s2,则:
倾角为30°的足够长光滑斜面下端与一足够长光滑水平面相接,连接处用一光滑小圆弧过渡,斜面上距水平面高度分别为h1=5m和h2=0.2m的两点上,各固定一小球A和B.某时刻由静止开始释放A球,经过一段时间t后,同样由静止开始释放B球.g取10m/s2,则: