题目内容
4.某行星自转角速度为ω0,一颗低轨道卫星环绕该行星做匀速圆周运动,若已知卫星的线速度v,向心加速度a和万有引力常量G,则由此可推算出( )| A. | 卫星的轨道半径为$\frac{{v}^{2}}{a}$ | |
| B. | 卫星运行的周期为$\frac{2π}{{ω}_{0}}$ | |
| C. | 行星的质量为$\frac{{v}^{4}}{Ga}$ | |
| D. | 行星的同步卫星的线速度为$\root{3}{\frac{{v}^{4}{ω}_{0}}{Ga}}$ |
分析 根据匀速圆周运动线速度与加速度的关系式,周期公式,以及向心加速度的公式可求解
解答 解:A、根据匀速圆周运动线速度与角速度的关系式a=$\frac{{v}^{2}}{r}$可求出轨道半径r=$\frac{{v}^{2}}{a}$,故A正确;
B、再根据公式T=$\frac{2πr}{v}$=$\frac{2πv}{a}$,由于低轨道卫星的角速度不一定等于自转的角速度,故B错误;
C、根据万有引力充当向心力知G$\frac{Mm}{{R}^{2}}$=ma,由于低轨道可以认为R=r,故M=$\frac{a{R}^{2}}{G}$=$\frac{a{r}^{2}}{G}$=$\frac{{v}^{4}}{Ga}$,故C正确;
D、由$\frac{GMm}{{r}^{2}}$=mω2r知r同步=$\root{3}{\frac{GM}{{ω}_{0}^{2}}}$,又v=ω0r同步=$\root{3}{\frac{{v}^{4}{ω}_{0}}{Ga}}$,故D正确;
故选:ACD
点评 此题考查万有引力充当向心力以及圆周运动物理量之间关系,要熟练掌握描述匀速圆周运动的物理量及对应的公式.

练习册系列答案
相关题目
15.某课题研究小组野外考察时登上一山峰,欲测出所处位置高度,做了如下实验:用细线拴好小石块系在树枝上做成一个简易单摆,用随身携带的钢卷尺测出悬点到石块重心的长度L:然后将石块拉开一个小角度,由静止释放,使其在竖直平面内摆动,用电子手表测出单摆完成n次全振动所用的时间t.若已知地球半径为R,海平面处重力加速度为g0由此可算出他们所处位置的海拔高度为( )
| A. | $\frac{2πn}{Rt}$$\sqrt{\frac{{g}_{0}}{L}}$-R | B. | $\frac{Rt}{2πn}$$\sqrt{\frac{L}{{g}_{0}}}$-R | C. | $\frac{2πRt}{n}$$\sqrt{\frac{L}{{g}_{0}}}$-R | D. | $\frac{Rt}{2πn}$$\sqrt{\frac{{g}_{0}}{L}}$-R |
19.下列说法正确的是( )
| A. | 康普顿效应说明光具有粒子性 | |
| B. | ${\;}_{92}^{235}$U的半衰期约为7亿年,随地球环境的变化,半衰期可能变短 | |
| C. | 在α射线、β射线、γ射线中,β射线是高速电子流,电离作用最强 | |
| D. | -束光照射到金属上,从金属表面逸出光电子,仅增加光的强度,光电子最大初动能不变 | |
| E. | 氢原子的核外电子由较高能级跃迁到较低能级时,要释放一定频率的光子,同时电子的动能增加,电势能减小 |
9.某列简谐横波在t1=0时刻的波形如图甲中实线所示,t2=3.0s时刻的波形如图甲中虚线所示,若图乙是图甲a、b、c、d四点中某质点的振动图象,则( )


| A. | 这列波沿x轴负方向传播 | |
| B. | 波速为0.5m/s | |
| C. | 图乙是质点b的振动图象 | |
| D. | 从t1=0s到t2=3.0s这段时间内,质点a通过的路程为1.5m | |
| E. | t3=9.5s时刻质点c沿y轴正向运动 |
16.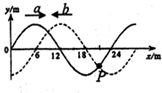 两列振幅为2cm、波长24cm和波速12m/s简谐横波a和b,分别沿x轴正方向和负方向传播.在t=0时刻的部分波形图如图所示,则( )
两列振幅为2cm、波长24cm和波速12m/s简谐横波a和b,分别沿x轴正方向和负方向传播.在t=0时刻的部分波形图如图所示,则( )
 两列振幅为2cm、波长24cm和波速12m/s简谐横波a和b,分别沿x轴正方向和负方向传播.在t=0时刻的部分波形图如图所示,则( )
两列振幅为2cm、波长24cm和波速12m/s简谐横波a和b,分别沿x轴正方向和负方向传播.在t=0时刻的部分波形图如图所示,则( )| A. | 图中x=15m处的质点是加强点 | |
| B. | 图中x=21m处的P质点经时间t=0.75出现速度最大值 | |
| C. | 此两列波相遇不能发生干涉现象 | |
| D. | 该两波如要发生明显的衍射现象,所遇到的障碍物的尺寸一般不大于2cm |
13.下列说法正确的是( )
| A. | 太阳辐射的能量主要来自太阳内部的轻核聚变 | |
| B. | 轻核聚变与重核裂变的能量均来自核反应过程中的质量亏损 | |
| C. | 原子核的比结合能越大表示该原子核越不稳定 | |
| D. | 实验表明,只要照射光的强度足够大,就一定能发生光电效应现象 | |
| E. | 光电管是应用光电效应原理制成的光电转换器件 |
 雨后彩虹是太阳光经过天空中小水珠折射后形成的,太阳光经过小水珠折射后某色光的光路如图所示.虚线是入射光线和出射光线延长线,α是两虚线夹角.由于太阳光是复色光,而水对不同色光折射率不同,光频率越高,折射率越大.则红色光在水珠中的传播速度最大;红光和紫光经过小水珠折射后,α红>α紫(选填“>”、“=”或“<”).
雨后彩虹是太阳光经过天空中小水珠折射后形成的,太阳光经过小水珠折射后某色光的光路如图所示.虚线是入射光线和出射光线延长线,α是两虚线夹角.由于太阳光是复色光,而水对不同色光折射率不同,光频率越高,折射率越大.则红色光在水珠中的传播速度最大;红光和紫光经过小水珠折射后,α红>α紫(选填“>”、“=”或“<”).
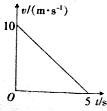 质量为2kg的物体置于水平面上,在运动方向上受拉力F作用沿水平面作匀变速运动,物体运动的v-t图象如图所示,若物体与地面间的动摩擦因数为0.5g,g取10m/s2,求5s内拉力与摩擦力做功各为多少?
质量为2kg的物体置于水平面上,在运动方向上受拉力F作用沿水平面作匀变速运动,物体运动的v-t图象如图所示,若物体与地面间的动摩擦因数为0.5g,g取10m/s2,求5s内拉力与摩擦力做功各为多少?