题目内容
15.某课题研究小组野外考察时登上一山峰,欲测出所处位置高度,做了如下实验:用细线拴好小石块系在树枝上做成一个简易单摆,用随身携带的钢卷尺测出悬点到石块重心的长度L:然后将石块拉开一个小角度,由静止释放,使其在竖直平面内摆动,用电子手表测出单摆完成n次全振动所用的时间t.若已知地球半径为R,海平面处重力加速度为g0由此可算出他们所处位置的海拔高度为( )| A. | $\frac{2πn}{Rt}$$\sqrt{\frac{{g}_{0}}{L}}$-R | B. | $\frac{Rt}{2πn}$$\sqrt{\frac{L}{{g}_{0}}}$-R | C. | $\frac{2πRt}{n}$$\sqrt{\frac{L}{{g}_{0}}}$-R | D. | $\frac{Rt}{2πn}$$\sqrt{\frac{{g}_{0}}{L}}$-R |
分析 单摆完成一次全振动的时间是一个周期.单摆完成n次全振动所用的时间t,求出周期.由单摆的周期公式得出重力加速度的表达式.根据重力等于万有引力,列式得出海拔高度与重力加速度的关系,即可求解.
解答 解:由题,单摆完成n次全振动所用的时间t,则得单摆的周期为 T=$\frac{t}{n}$.①
设山峰处重力加速度为g,由单摆的周期公式 T=2π$\sqrt{\frac{L}{g}}$ ②
又mg=G$\frac{Mm}{(R+h)^{2}}$,③
mg0=G$\frac{Mm}{{R}^{2}}$,④
由③④得:g=$\frac{{R}^{2}}{(R+h)^{2}}{g}_{0}$ ⑤
由①②⑤联立解得:h=$\frac{Rt}{2πn}$$\sqrt{\frac{{g}_{0}}{L}}$-R
故选:D.
点评 单摆的周期采用累积法测量,周期的表达式为T=$\frac{t}{n}$.关键要抓住单摆周期与万有引力之间联系的纽带:重力加速度g,由重力等于万有引力,研究重力加速度与高度的关系.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
5. 用等势线描绘电场,是研究电场的一种科学方法.如图所示,A、B为水平放置的平行板电容器,两板间所加电压为120V,两板间距为12cm,图中所绘实线为平行板电容器部分等势线.a、b是等 势线上的两点,b点的场强大小为Eb.下列判断可能正确的是( )
用等势线描绘电场,是研究电场的一种科学方法.如图所示,A、B为水平放置的平行板电容器,两板间所加电压为120V,两板间距为12cm,图中所绘实线为平行板电容器部分等势线.a、b是等 势线上的两点,b点的场强大小为Eb.下列判断可能正确的是( )
 用等势线描绘电场,是研究电场的一种科学方法.如图所示,A、B为水平放置的平行板电容器,两板间所加电压为120V,两板间距为12cm,图中所绘实线为平行板电容器部分等势线.a、b是等 势线上的两点,b点的场强大小为Eb.下列判断可能正确的是( )
用等势线描绘电场,是研究电场的一种科学方法.如图所示,A、B为水平放置的平行板电容器,两板间所加电压为120V,两板间距为12cm,图中所绘实线为平行板电容器部分等势线.a、b是等 势线上的两点,b点的场强大小为Eb.下列判断可能正确的是( )| A. | Eb=1000V/m,电子由a点移到b点电势能增加60eV | |
| B. | Eb=1000V/m,电子由a点移到b点电势能减少30eV | |
| C. | Eb=700V/m,电子由a点移到b点电势能增加60eV | |
| D. | Eb=700V/m,电子由a点移到b点电势能减少30eV |
6.如图1所示,将一小物块从斜面顶端由静止释放,小物块经过A点后到达底端B点,小明测出了AB之间的距离和小物块经过AB所用的时间,改变A的位置,测出多组AB间距及经过AB所用的时间t,小明作出了AB段平均速度$\overline{v}$与经过时间t的图象,下列说法正确的是( )


| A. | 由图象可求出小物块到达B点的速度 | |
| B. | 由图象可知小物块做匀减速直线运动 | |
| C. | 图线和t轴所围的面积等于斜面的长度 | |
| D. | 有图象可知小物块运动的加速度大小等于$\frac{v}{2{t}_{0}}$ |
10.如图甲所示,一质量为1kg的带电小木块放置在绝缘的粗糙水平地面上做直线运动.木块和地而间的动摩擦因数为μ=0.4,空间存在水平方向的匀强电场,场强方向和大小均可变,t=0时刻小木块受到电场力F的作用.且向右运动,其速度-时间图象如图乙所示,取向右为正方向.则( )


| A. | 在0~4s内小木块做匀减速运动 | B. | 在2~4s内电场力F的方向向右 | ||
| C. | 在0~6s内电场力F一直做正功 | D. | 在0~6s内小木块的位移为4m |
20.下列说法中正确的( )
| A. | 康普顿效应说明光具粒子性,光子具有动量 | |
| B. | 光的偏振现象说明光是一种横波 | |
| C. | 在光的双链干涉实验中,若仅将入射光由绿光改为红光,则干涉条纹间距变宽 | |
| D. | 麦克斯韦预言电磁波存在,后来由他又用实验证实电磁波的存在 |
4.某行星自转角速度为ω0,一颗低轨道卫星环绕该行星做匀速圆周运动,若已知卫星的线速度v,向心加速度a和万有引力常量G,则由此可推算出( )
| A. | 卫星的轨道半径为$\frac{{v}^{2}}{a}$ | |
| B. | 卫星运行的周期为$\frac{2π}{{ω}_{0}}$ | |
| C. | 行星的质量为$\frac{{v}^{4}}{Ga}$ | |
| D. | 行星的同步卫星的线速度为$\root{3}{\frac{{v}^{4}{ω}_{0}}{Ga}}$ |


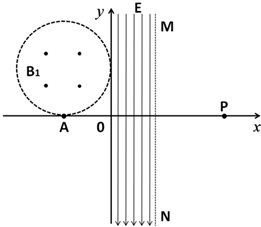 如图所示,第二象限,半径为r的圆形区域内存在方向垂直纸面向外的匀强磁场,磁场边界恰好与两坐标轴相切.x轴上切点A处有一粒子源,能个向x轴上方发射速率相等,均为v,质量为m,电量为+q的粒子,粒子重力不计.圆形区域磁场的磁感应强度B1=$\frac{mv}{qr}$,y轴右侧0<y<r的范围内存在沿y轴负方向的匀强电场,已知某粒子从A处沿+y方向射入磁场后,再进入匀强电场,发现粒子从电场右边界MN射出,速度方向与x轴正方向成45°角斜向下,求:
如图所示,第二象限,半径为r的圆形区域内存在方向垂直纸面向外的匀强磁场,磁场边界恰好与两坐标轴相切.x轴上切点A处有一粒子源,能个向x轴上方发射速率相等,均为v,质量为m,电量为+q的粒子,粒子重力不计.圆形区域磁场的磁感应强度B1=$\frac{mv}{qr}$,y轴右侧0<y<r的范围内存在沿y轴负方向的匀强电场,已知某粒子从A处沿+y方向射入磁场后,再进入匀强电场,发现粒子从电场右边界MN射出,速度方向与x轴正方向成45°角斜向下,求: