题目内容
5. 如图,一个物体静止放在水平面上,在跟竖直方向成θ角为37度的斜向下的推力F=20N的作用下沿水平移动的距离s=5m,若物体的质量为m=0.4kg,物体与地面之间的动摩擦因数μ=0.2,(g=10m/s2,sin37.=0.6,cos37.=0.8)求:
如图,一个物体静止放在水平面上,在跟竖直方向成θ角为37度的斜向下的推力F=20N的作用下沿水平移动的距离s=5m,若物体的质量为m=0.4kg,物体与地面之间的动摩擦因数μ=0.2,(g=10m/s2,sin37.=0.6,cos37.=0.8)求:(1)力F做的功
(2)摩擦力做的功
(3)物体沿水平面移动了距离s=5m时的动能.
分析 (1)据功的定义式W=Fscosα求解即可;(2)据功的定义式和滑动摩擦力求出即可.(3)利用动能定理求出移动5米的动能即可.
解答 解:(1)据题意和图可知,力的方向与位移方向的夹角:α=90°-θ
功的定义式W=Fscosα=20×5×0.6J=60J
(2)功的定义式W=Fscosα得:Wf=-fs…①
据题知:FN=mg+Fcosθ…②
又因为:f=uFN…③
联立①②③代入数据解得:Wf=-20J
(3)据动能定理得:W+Wf=Ek
所以:Ek=60J-20J=40J
答:(1)力F做的功60J.
(2)摩擦力做的功-20J.
(3)物体沿水平面移动了距离s=5m时的动能40J.
点评 此题注要考查了功的求法和滑动摩擦力的表述方法,此题实质是动能定理的应用,只是把过程分解了;还需注意角度间的关系.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
7. 如图所示,倾角为的斜面体C置于水平地面上,通过细绳跨过光滑的定滑轮和物体A相连接,连接B的一段细绳与斜面平行,A、B、C都处于静止状态.则( )
如图所示,倾角为的斜面体C置于水平地面上,通过细绳跨过光滑的定滑轮和物体A相连接,连接B的一段细绳与斜面平行,A、B、C都处于静止状态.则( )
 如图所示,倾角为的斜面体C置于水平地面上,通过细绳跨过光滑的定滑轮和物体A相连接,连接B的一段细绳与斜面平行,A、B、C都处于静止状态.则( )
如图所示,倾角为的斜面体C置于水平地面上,通过细绳跨过光滑的定滑轮和物体A相连接,连接B的一段细绳与斜面平行,A、B、C都处于静止状态.则( )| A. | B受到C的摩擦力一定不为零 | |
| B. | C受地面的摩擦力一定为零 | |
| C. | C有沿地面向右滑动的趋势,一定受到地面向左的摩擦力 | |
| D. | 将细绳剪断,若B依然静止在斜面上,此时地面对C的摩擦力水平向左 |
13.下列说法正确的是( )
| A. | 波在传播过程中,质点的振动频率等于波源的振动频率 | |
| B. | 当某列声波发生多普勒效应时,相应声源的振动频率一定发生变化 | |
| C. | 物体做受迫振动时,驱动力频率越高,受迫振动的物体振幅越大 | |
| D. | 爱因斯坦狭义相对论指出,真空中的光速在不同的惯性参考系中都是相同的 | |
| E. | X射线的频率比无线电波的频率高 |
20. 如图所示,球与斜面光滑接触,用水平推力F缓慢推动斜面使球升到A端(此时绳子接近水平位置),在此过程中,绳子的拉力为T,球对斜面的压力为N,则( )
如图所示,球与斜面光滑接触,用水平推力F缓慢推动斜面使球升到A端(此时绳子接近水平位置),在此过程中,绳子的拉力为T,球对斜面的压力为N,则( )
 如图所示,球与斜面光滑接触,用水平推力F缓慢推动斜面使球升到A端(此时绳子接近水平位置),在此过程中,绳子的拉力为T,球对斜面的压力为N,则( )
如图所示,球与斜面光滑接触,用水平推力F缓慢推动斜面使球升到A端(此时绳子接近水平位置),在此过程中,绳子的拉力为T,球对斜面的压力为N,则( )| A. | N不断增大,T先减小后增大 | B. | N不断增大,T不断减小 | ||
| C. | N不变,T不断增大 | D. | N不变,T先减小后增大 |
17.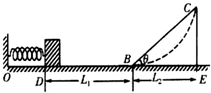 如图是一探究功能关系的实验装置,水平面与斜面交于B点,轻弹簧左端固定于竖直墙面,用质量为m的滑块压缩弹簧至D点,由静止释放,滑块脱离弹簧后恰好能滑到斜面最高点C;然后,去掉斜面改用圆弧形轨道,让滑块由相同位置D静止释放,滑块沿圆弧轨道上升至某点.已知水平面、斜面BC、圆弧形轨道和滑块间的动摩擦因数均为μ,BD=L1,斜面底边BE=L2,倾角为θ.滑块可视为质点,不计滑块在B点的机械能损失,则( )
如图是一探究功能关系的实验装置,水平面与斜面交于B点,轻弹簧左端固定于竖直墙面,用质量为m的滑块压缩弹簧至D点,由静止释放,滑块脱离弹簧后恰好能滑到斜面最高点C;然后,去掉斜面改用圆弧形轨道,让滑块由相同位置D静止释放,滑块沿圆弧轨道上升至某点.已知水平面、斜面BC、圆弧形轨道和滑块间的动摩擦因数均为μ,BD=L1,斜面底边BE=L2,倾角为θ.滑块可视为质点,不计滑块在B点的机械能损失,则( )
 如图是一探究功能关系的实验装置,水平面与斜面交于B点,轻弹簧左端固定于竖直墙面,用质量为m的滑块压缩弹簧至D点,由静止释放,滑块脱离弹簧后恰好能滑到斜面最高点C;然后,去掉斜面改用圆弧形轨道,让滑块由相同位置D静止释放,滑块沿圆弧轨道上升至某点.已知水平面、斜面BC、圆弧形轨道和滑块间的动摩擦因数均为μ,BD=L1,斜面底边BE=L2,倾角为θ.滑块可视为质点,不计滑块在B点的机械能损失,则( )
如图是一探究功能关系的实验装置,水平面与斜面交于B点,轻弹簧左端固定于竖直墙面,用质量为m的滑块压缩弹簧至D点,由静止释放,滑块脱离弹簧后恰好能滑到斜面最高点C;然后,去掉斜面改用圆弧形轨道,让滑块由相同位置D静止释放,滑块沿圆弧轨道上升至某点.已知水平面、斜面BC、圆弧形轨道和滑块间的动摩擦因数均为μ,BD=L1,斜面底边BE=L2,倾角为θ.滑块可视为质点,不计滑块在B点的机械能损失,则( )| A. | 释放滑块前弹簧的弹性势能为μmg(L1+L2)+mgL2tanθ | |
| B. | 滑块由D点滑到B点时动能为μmgL2+mgL2tanθ | |
| C. | 在两次运动过程中滑块上升的高度相同 | |
| D. | 在两次运动过程中滑块的机械能损失均为μmg(L1+$\frac{{L}_{2}}{cosθ}$) |
14. 简谐横波某时刻的波形如图所示,P为介质中的一个质点,波沿x轴的正方向传播.下列说法正确的是( )
简谐横波某时刻的波形如图所示,P为介质中的一个质点,波沿x轴的正方向传播.下列说法正确的是( )
 简谐横波某时刻的波形如图所示,P为介质中的一个质点,波沿x轴的正方向传播.下列说法正确的是( )
简谐横波某时刻的波形如图所示,P为介质中的一个质点,波沿x轴的正方向传播.下列说法正确的是( )| A. | 质点P此时刻的速度沿y轴的负方向 | |
| B. | 质点P此时刻的加速度沿y轴的正方向 | |
| C. | 再过半个周期时,质点P的位移为负值 | |
| D. | 经过一个周期,质点P通过的路程为2a |
15. 如图所示,金属棒MN两端由等长的轻质细线水平悬挂,处于竖直向上的匀强磁场中,棒中通以由M向N的电流,平衡时两悬线与竖直方向夹角均为θ.如果仅改变下列某一个条件,θ角的相应变化情况是( )
如图所示,金属棒MN两端由等长的轻质细线水平悬挂,处于竖直向上的匀强磁场中,棒中通以由M向N的电流,平衡时两悬线与竖直方向夹角均为θ.如果仅改变下列某一个条件,θ角的相应变化情况是( )
 如图所示,金属棒MN两端由等长的轻质细线水平悬挂,处于竖直向上的匀强磁场中,棒中通以由M向N的电流,平衡时两悬线与竖直方向夹角均为θ.如果仅改变下列某一个条件,θ角的相应变化情况是( )
如图所示,金属棒MN两端由等长的轻质细线水平悬挂,处于竖直向上的匀强磁场中,棒中通以由M向N的电流,平衡时两悬线与竖直方向夹角均为θ.如果仅改变下列某一个条件,θ角的相应变化情况是( )| A. | 棒中的电流变大,θ角变小 | B. | 两悬线等长变短,θ角变小 | ||
| C. | 金属棒质量变大,θ角变小 | D. | 磁感应强度变大,θ角变小 |
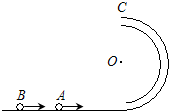 如图所示,半径为R,内径很小的光滑半圆细管竖直放置,两个质量均为m的小球A、B,以不同的速率进入管内,若A球通过圆周最高点C,对管壁上部的压力为3mg,B球通过最高点C时,对管壁内、外侧的压力均为0,求A、B球落地点间的距离.
如图所示,半径为R,内径很小的光滑半圆细管竖直放置,两个质量均为m的小球A、B,以不同的速率进入管内,若A球通过圆周最高点C,对管壁上部的压力为3mg,B球通过最高点C时,对管壁内、外侧的压力均为0,求A、B球落地点间的距离. 如图所示,空间内有方向垂直纸面(竖直面)向里的有界匀强磁场区域Ⅰ、Ⅱ,磁感应强度大小未知.区域I内有竖直向上的匀强电场,区域Ⅱ内有水平向右的匀强电场,两区域内的电场强度大小相等.现有一质量m=1×10-2kg、电荷量q=1×10-2C的带正电滑块从区域I左侧边界N点以v0=4m/s的初速度沿光滑的水平面向右运动,进入区域Ⅰ后,滑块立即在区域I竖直平面内做匀速圆周运动,并落在与边界MN相距L=2m的A点,取重力加速度g=10m/s2.
如图所示,空间内有方向垂直纸面(竖直面)向里的有界匀强磁场区域Ⅰ、Ⅱ,磁感应强度大小未知.区域I内有竖直向上的匀强电场,区域Ⅱ内有水平向右的匀强电场,两区域内的电场强度大小相等.现有一质量m=1×10-2kg、电荷量q=1×10-2C的带正电滑块从区域I左侧边界N点以v0=4m/s的初速度沿光滑的水平面向右运动,进入区域Ⅰ后,滑块立即在区域I竖直平面内做匀速圆周运动,并落在与边界MN相距L=2m的A点,取重力加速度g=10m/s2.