题目内容
18.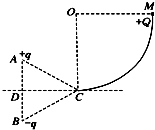 如图所示,竖直平面内$\frac{1}{4}$光滑圆弧轨道半径为R,等边三角形ABC的边长为L,顶点C恰好位于圆周最低点,CD是AB边的中垂线.在A、B两顶点上放置一对等量异种电荷.现把质量为m带电荷量为+Q的小球由圆弧的最高点M处静止释放,到最低点C时速度为v0.不计+Q对原电场的影响,取无穷远处为零电势,静电力常量为k,则( )
如图所示,竖直平面内$\frac{1}{4}$光滑圆弧轨道半径为R,等边三角形ABC的边长为L,顶点C恰好位于圆周最低点,CD是AB边的中垂线.在A、B两顶点上放置一对等量异种电荷.现把质量为m带电荷量为+Q的小球由圆弧的最高点M处静止释放,到最低点C时速度为v0.不计+Q对原电场的影响,取无穷远处为零电势,静电力常量为k,则( )| A. | 小球在圆弧轨道上运动过程机械能守恒 | |
| B. | C点电势与D点电势相同 | |
| C. | M点电势为$\frac{1}{2Q}$(mv02-2mgR) | |
| D. | 小球对轨道最低点C处的压力大小为mg+m$\frac{{{v}_{0}}^{2}}{R}$+k$\frac{Qq}{{L}^{2}}$ |
分析 此题属于电场力与重力场的复合场,根据机械能守恒的条件:只有重力或弹力做功,分析机械能是否守恒.根据电场线的分布情况,分析C与D两点的电势关系.由动能定理求MC间的电势差,从而求得M点的电势.由牛顿定律求小球对轨道最低点C处的压力大小.
解答 解:A、小球在圆弧轨道上运动的过程中,重力对小球做功,还有电场力对小球要做功,所以其机械能不守恒,故A错误;
B、C、D两点位于AB两电荷产生的电场的等势能面上,电势相同,故B正确;
C、小球从M到C的过程中,根据动能定理得:qUMC+mgR=$\frac{1}{2}$mv02,取无穷远处电势为零,可知,CD所在等势面电势为零,C点的电势为零.由UMC=φM-φC,
联立两式解得,M点的电势为 φM=$\frac{1}{2Q}$(mv02-2mgR),故C正确;
D、小球对轨道最低点C处时,+q和-q两个点对小球的库仑力大小均为k$\frac{Qq}{{L}^{2}}$,它们的夹角为120°,根据几何知识可知库仑力的合力大小为 k$\frac{Qq}{{L}^{2}}$,方向向下.
根据牛顿第二定律得 N-k$\frac{Qq}{{L}^{2}}$-mg=m$\frac{{v}_{0}^{2}}{R}$,得 N=mg+m$\frac{{{v}_{0}}^{2}}{R}$+k$\frac{Qq}{{L}^{2}}$,由牛顿第三定律知:小球对轨道的压力为mg+m$\frac{{{v}_{0}}^{2}}{R}$+k$\frac{Qq}{{L}^{2}}$,故D正确;
故选:BCD
点评 此题的难度在于计算小球到最低点时的电场力的大小,注意AB处有等量异种电荷,CD是AB边的中垂线,则CD是一条等势线,且一直延伸到无穷远处.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
13.如图所示是静电场的一部分电场线分布,下列说法中正确的是( )


| A. | 点电荷q在A点处受到的静电力比在B点处受到的静电力大 | |
| B. | 这个电场可能是负点电荷的电场 | |
| C. | 点电荷q在A点处的瞬时加速度比在B点处的瞬时加速度小(不计重力) | |
| D. | 负电荷在B点处受到的静电力的方向沿B点切线方向 |
3. 如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点仅在静电力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )
如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点仅在静电力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )
 如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点仅在静电力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )
如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点仅在静电力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )| A. | 三个等势面中,a的电势最高 | B. | 带电质点通过P点时的电势能较大 | ||
| C. | 带电质点通过P点时的动能较大 | D. | 带电质点通过P点时的加速度较大 |
7. 如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点仅在电场力作用下通过该区域时的运动轨迹,P、R、Q是这条轨迹上的三点,R同时也在等势面b上,据此可知( )
如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点仅在电场力作用下通过该区域时的运动轨迹,P、R、Q是这条轨迹上的三点,R同时也在等势面b上,据此可知( )
 如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点仅在电场力作用下通过该区域时的运动轨迹,P、R、Q是这条轨迹上的三点,R同时也在等势面b上,据此可知( )
如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点仅在电场力作用下通过该区域时的运动轨迹,P、R、Q是这条轨迹上的三点,R同时也在等势面b上,据此可知( )| A. | 三个等势面中,a的电势最低 | |
| B. | 带电质点在P点的电势能比在Q点的大 | |
| C. | 带电质点在P点的动能与电势能之和比在Q点的小 | |
| D. | 带电质点在R点的加速度方向垂直于等势面b |
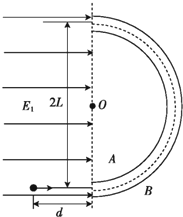 如图所示,两块直径为2L的同心半圆形带电金属板A、B固定在竖直平面内,两板间的距离很近,可认为A、B间的电场场强大小处处相等、方向都指向圆心O.在A、B左侧有方向水平向右、场强大小为E的匀强电场.现从正对A、B板间隙、到两板的一端距离为d处由静止释放一个质量为m、电荷量为q的带正电微粒(不计重力),发现此微粒恰能在两板间运动而不与板发生相互作用.
如图所示,两块直径为2L的同心半圆形带电金属板A、B固定在竖直平面内,两板间的距离很近,可认为A、B间的电场场强大小处处相等、方向都指向圆心O.在A、B左侧有方向水平向右、场强大小为E的匀强电场.现从正对A、B板间隙、到两板的一端距离为d处由静止释放一个质量为m、电荷量为q的带正电微粒(不计重力),发现此微粒恰能在两板间运动而不与板发生相互作用. 


 某班级同学用如图(a)所示的装置验证加速度a和力F、质量m 的关系.甲、乙两辆小车放在倾斜轨道上,小车甲上固定一个力传感器,小车乙上固定一个加速度传感器(可以测量乙在任意时刻的加速度大小),力传感器和小车乙之间用-根不可伸长的细线连接(细绳与倾斜轨道平行),在弹簧拉力的作用下两辆小车 一起开始运动,利用两个传感器可以釆集记录同一时刻小车乙受到的拉力和加速度的大小.
某班级同学用如图(a)所示的装置验证加速度a和力F、质量m 的关系.甲、乙两辆小车放在倾斜轨道上,小车甲上固定一个力传感器,小车乙上固定一个加速度传感器(可以测量乙在任意时刻的加速度大小),力传感器和小车乙之间用-根不可伸长的细线连接(细绳与倾斜轨道平行),在弹簧拉力的作用下两辆小车 一起开始运动,利用两个传感器可以釆集记录同一时刻小车乙受到的拉力和加速度的大小. 一空间探测器从某一星球表面竖直升空,若探测器升空一段时间后,发动机突然关闭,其速度随时间的变化情况如图所示,图线上A、B、C 三点对应的时刻分别为 9s、25s 和 45s.已知该星球表面没有空气.试求:
一空间探测器从某一星球表面竖直升空,若探测器升空一段时间后,发动机突然关闭,其速度随时间的变化情况如图所示,图线上A、B、C 三点对应的时刻分别为 9s、25s 和 45s.已知该星球表面没有空气.试求: