题目内容
6.在探究物体的加速度a与物体所受外力F、物体质量M间的关系时,采用如图a所示的实验装置.小车及车中的砝码质量用M表示,盘及盘中的砝码质量用m表示.
(1)若已平衡好摩擦,在小车做匀加速直线运动过程中绳子拉力T=$\frac{M}{M+m}mg$,当M与m的大小关系满足M>>m时,才可以认为绳对小车的拉力大小等于盘和盘中砝码的重力.
(2)某一组同学先保持盘及盘中的砝码质量m一定来做实验,其具体操作步骤如下,以下做法正确的是C.
A.平衡摩擦力时,应将盘及盘中的砝码用细绳通过定滑轮系在小车上
B.每次改变小车的质量时,需要重新平衡摩擦力
C.实验时,先接通打点计时器的电源,再放开小车
D.用天平测出m以及小车质量M,小车运动的加速度可直接用公式a=$\frac{mg}{M}$求出
(3)某小组同学保持小车及车中的砝码质量M一定,探究加速度a与所受外力F的关系,由于他们操作不当,这组同学得到的a-F关系图象如图b所示,其原因是:①平衡摩擦力不够或没有平衡摩擦力;②没有满足M>>m
(4)图c是某次实验中得到的纸带.已知打点计时器使用的交流电频率为50Hz,每相邻两个计数点间还有4个点未画出,求出小车下滑的加速度为1.58rn/s2.(结果保留三位有效数字)

分析 解决实验问题首先要掌握该实验原理,了解实验的操作步骤和数据处理以及注意事项.
该实验采用的是控制变量法研究,其中加速度、质量、合力三者的测量很重要;
根据连续相等时间内的位移之差是一恒量,运用逐差法求出小车的加速度.
解答 解:(1)该实验的研究对象是小车,采用控制变量法研究.当质量一定时,研究小车的加速度和小车所受合力的关系.那么小车的合力怎么改变和测量呢?为消除摩擦力对实验的影响,可以把木板D的右端适当垫高,以使小车的重力沿斜面分力和摩擦力抵消,那么小车的合力就是绳子的拉力.
根据牛顿第二定律得:
对m:mg-T=ma
对M:T=Ma
解得:T=$\frac{M}{M+m}$mg
当M>>m时,即当砝码和盘的总重力要远小于小车的重力,绳子的拉力近似等于砝码和盘的总重力.
(2)A、平衡摩擦力时,应将绳从小车上拿去,轻轻推动小车,是小车沿木板运动,通过打点计时器打出来的纸带判断小车是否匀速运动.故A错误.
B、每次改变小车的质量时,小车的重力沿斜面分力和摩擦力仍能抵消,不需要重新平衡摩擦力.故B错误.
C、实验时,若先放开小车,再接通打点计时器电源,由于小车运动较快,可能会使打出来的点很少,不利于数据的采集和处理.故C正确.
D、小车运动的加速度是利用打点计时器测量,如果用天平测出m以及小车质量M,直接用公式求出,这是在直接运用牛顿第二定律计算的,而我们实验是在探究加速度与物体所受合外力和质量间的关系.故D错误.
故选C
(3)当F≠0时,a=0.也就是说当绳子上有拉力时小车的加速度还为0,说明小车的摩擦力与绳子的拉力抵消呢.该组同学实验操作中遗漏了平衡摩擦力或平衡摩擦力不足这个步骤,随着F的增大,即砂和砂桶质量的增大,不在满足砂和砂桶远小于小车的质量,因此曲线上部出现弯曲现象.
(4)由于每相邻两个计数点间还有4个点没有画出,所以相邻的计数点间的时间间隔T=0.1s,
根据△x=aT2,运用逐差法得,
a=$\frac{{x}_{CF}-{x}_{OC}}{9{T}^{2}}$=$\frac{(7.57+9.10+10.71)-(2.80+4.40+5.95)}{9×0.{1}^{2}}$×10-2=1.58m/s2.
故答案为:(1)$\frac{M}{M+m}mg$,M>>m; (2)C;
(3)①平衡摩擦力不够或没有平衡摩擦力;②没有满足M>>m; (4)1.58.
点评 教科书本上的实验,我们要从实验原理、实验仪器、实验步骤、实验数据处理、实验注意事项这几点去搞清楚,同时注意整体法和隔离法的应用.
注意其中平衡摩擦力的原因以及做法在实验中应当清楚.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 一带电粒子从电场中的A点运动到B点,径迹如图中虚线所示,图中实线为电场线,不计粒子所受重力,则( )
一带电粒子从电场中的A点运动到B点,径迹如图中虚线所示,图中实线为电场线,不计粒子所受重力,则( )| A. | 粒子带正电 | B. | A点的场强小于B点场强 | ||
| C. | 粒子加速度逐渐减小 | D. | 粒子的速度一定在不断增大 |
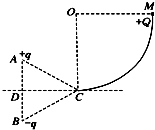 如图所示,竖直平面内$\frac{1}{4}$光滑圆弧轨道半径为R,等边三角形ABC的边长为L,顶点C恰好位于圆周最低点,CD是AB边的中垂线.在A、B两顶点上放置一对等量异种电荷.现把质量为m带电荷量为+Q的小球由圆弧的最高点M处静止释放,到最低点C时速度为v0.不计+Q对原电场的影响,取无穷远处为零电势,静电力常量为k,则( )
如图所示,竖直平面内$\frac{1}{4}$光滑圆弧轨道半径为R,等边三角形ABC的边长为L,顶点C恰好位于圆周最低点,CD是AB边的中垂线.在A、B两顶点上放置一对等量异种电荷.现把质量为m带电荷量为+Q的小球由圆弧的最高点M处静止释放,到最低点C时速度为v0.不计+Q对原电场的影响,取无穷远处为零电势,静电力常量为k,则( )| A. | 小球在圆弧轨道上运动过程机械能守恒 | |
| B. | C点电势与D点电势相同 | |
| C. | M点电势为$\frac{1}{2Q}$(mv02-2mgR) | |
| D. | 小球对轨道最低点C处的压力大小为mg+m$\frac{{{v}_{0}}^{2}}{R}$+k$\frac{Qq}{{L}^{2}}$ |
 一实验兴趣小组做了一次实验,实验时让某同学从桌子上跳下,自由下落H后双脚触地,他顺势弯曲双腿,他的重心又下降了h后停住,利用传感器和计算机显示该同学受到地面的支持力F随时间变化的图象如图所示.根据图象提供的信息,以下判断正确的是( )
一实验兴趣小组做了一次实验,实验时让某同学从桌子上跳下,自由下落H后双脚触地,他顺势弯曲双腿,他的重心又下降了h后停住,利用传感器和计算机显示该同学受到地面的支持力F随时间变化的图象如图所示.根据图象提供的信息,以下判断正确的是( )| A. | t2时刻该同学的脚刚接触地面 | |
| B. | t3时刻该同学的加速度为零 | |
| C. | 在t2至t3时间内该同学处于下落阶段 | |
| D. | 在t3至t4时间内该同学处于加速下落阶段 |
 一斜面AB长为5m,倾角为30°,一质量为2kg的小物体(大小不计)从斜面顶端A点由静止释放,如图所示.斜面与物体间的动摩擦因数为$\frac{\sqrt{3}}{6}$,求
一斜面AB长为5m,倾角为30°,一质量为2kg的小物体(大小不计)从斜面顶端A点由静止释放,如图所示.斜面与物体间的动摩擦因数为$\frac{\sqrt{3}}{6}$,求 在图所示电路中,已知Uac=3V,Uab=2v,试分别以a点和c点作为参考点,求b点的电位和b,c两点间的电压.
在图所示电路中,已知Uac=3V,Uab=2v,试分别以a点和c点作为参考点,求b点的电位和b,c两点间的电压.
