题目内容
17.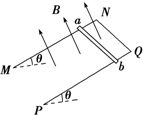 如图,足够长的U形光滑金属导轨平面与水平面成θ角(0<θ<90°),其中MN与PQ平行且间距为L,导轨平面与磁感应强度为B的匀强磁场垂直,导轨电阻不计.金属棒ab由静止开始沿导轨下滑,并与两导轨始终保持垂直且良好接触,ab棒接入电路的电阻为R,当流过ab棒某一横截面的电荷量为q时,金属棒的速度大小为v,则金属棒ab在这一过程中( )
如图,足够长的U形光滑金属导轨平面与水平面成θ角(0<θ<90°),其中MN与PQ平行且间距为L,导轨平面与磁感应强度为B的匀强磁场垂直,导轨电阻不计.金属棒ab由静止开始沿导轨下滑,并与两导轨始终保持垂直且良好接触,ab棒接入电路的电阻为R,当流过ab棒某一横截面的电荷量为q时,金属棒的速度大小为v,则金属棒ab在这一过程中( )| A. | ab棒运动的平均速度大小为$\frac{1}{2}$v | B. | 沿导轨方向的位移大小为$\frac{qR}{BL}$ | ||
| C. | 产生的焦耳热为qBLv | D. | 受到的最大安培力大小为$\frac{{{B^2}{L^2}v}}{R}$ |
分析 金属棒ab由静止开始沿导轨下滑,做加速度逐渐减小的变加速运动.由牛顿第二定律,法拉第电磁感应定律、能量守恒定律等研究处理.
解答 解:A、金属棒ab开始做加速运动,速度增大,感应电动势增大,所以感应电流也增大,导致金属棒受到的安培力增大,所以加速度减小,即金属板做加速度逐渐减小的变加速运动,
因此运动的平均速度大小大于$\frac{1}{2}$v,故A错误;
B、由电量计算公式q=It=$\frac{E}{R}$t=$\frac{n△∅}{R}$=$\frac{BLs}{R}$ 可得,下滑的位移大小为s=$\frac{qR}{BL}$,故B正确;
C、产生的焦耳热Q=I2Rt=qIR,而这里的电流I比棒的速度大小为v时的电流I′=$\frac{BLv}{R}$小,故这一过程产生的焦耳热小于qBLv.故C错误;
D、金属棒ab受到的最大安培力大小为F=BIL=B•$\frac{BLv}{R}$•L=$\frac{{B}^{2}{L}^{2}v}{R}$,故D正确.
故选:BD.
点评 电磁感应综合题中,常常用到这个经验公式:感应电量q=$\frac{n△∅}{R+r}$常用来求位移,但在计算题中,不能直接作为公式用,要推导.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
3.下列物理量为矢量的是( )
| A. | 长度 | B. | 速度 | C. | 时间 | D. | 质量 |
4. 如图所示,装有足够多的沙子的圆筒上方有大小相同的实心钢球和木球,现从同一高度由静止释放,不计空气阻力,下列说法正确的是( )
如图所示,装有足够多的沙子的圆筒上方有大小相同的实心钢球和木球,现从同一高度由静止释放,不计空气阻力,下列说法正确的是( )
 如图所示,装有足够多的沙子的圆筒上方有大小相同的实心钢球和木球,现从同一高度由静止释放,不计空气阻力,下列说法正确的是( )
如图所示,装有足够多的沙子的圆筒上方有大小相同的实心钢球和木球,现从同一高度由静止释放,不计空气阻力,下列说法正确的是( )| A. | 钢球比木球先到达沙子表面 | |
| B. | 钢球到达沙子表面的速度比木球大 | |
| C. | 钢球陷入沙子全过程的速度变化量比木球大 | |
| D. | 钢球陷入沙子全过程克服阻力做的功比木球大 |
2. 如图所示,平行金属板内存在匀强电场.一个电量为+q、质量为m的粒子(不计重力)以初速度v0从A点沿水平方向射入电场,而从B点射出时速度为v,则( )
如图所示,平行金属板内存在匀强电场.一个电量为+q、质量为m的粒子(不计重力)以初速度v0从A点沿水平方向射入电场,而从B点射出时速度为v,则( )
 如图所示,平行金属板内存在匀强电场.一个电量为+q、质量为m的粒子(不计重力)以初速度v0从A点沿水平方向射入电场,而从B点射出时速度为v,则( )
如图所示,平行金属板内存在匀强电场.一个电量为+q、质量为m的粒子(不计重力)以初速度v0从A点沿水平方向射入电场,而从B点射出时速度为v,则( )| A. | 若该粒子以速度-v从B点射入,则刚好以速度-v0从A点射出 | |
| B. | 若该粒子以速度-v0从B点射入,它刚好以速度-v从A点射出 | |
| C. | 若将-q、质量为m的粒子以速度v0从A点射入,它刚好以速度v从B点射出 | |
| D. | 若将-q、质量为m的粒子以速度-v从B点射入,它刚好以速度-v0从A点射出 |
9.下列物理量是不是矢量的是( )
| A. | 时间 | B. | 加速度 | C. | 位移 | D. | 速度 |
6. 如图所示,建筑工地上载人升降机用不计质量的细钢绳跨过定滑轮与一电动机相连,通电后电动机带动升降机沿竖直方向先匀加速上升后匀速上升.摩擦及空气阻力均不计.则( )
如图所示,建筑工地上载人升降机用不计质量的细钢绳跨过定滑轮与一电动机相连,通电后电动机带动升降机沿竖直方向先匀加速上升后匀速上升.摩擦及空气阻力均不计.则( )
 如图所示,建筑工地上载人升降机用不计质量的细钢绳跨过定滑轮与一电动机相连,通电后电动机带动升降机沿竖直方向先匀加速上升后匀速上升.摩擦及空气阻力均不计.则( )
如图所示,建筑工地上载人升降机用不计质量的细钢绳跨过定滑轮与一电动机相连,通电后电动机带动升降机沿竖直方向先匀加速上升后匀速上升.摩擦及空气阻力均不计.则( )| A. | 升降机匀加速上升过程中,升降机底板对人做的功等于人增加的动能 | |
| B. | 升降机匀加速上升过程中,升降机底板对人做的功等于人增加的机械能 | |
| C. | 升降机匀速上升过程中,升降机底板对人做的功等于人增加的机械能 | |
| D. | 升降机上升的全过程中,升降机拉力做的功大于升降机和人增加的机械能 |
7.下列关于磁通量的说法正确的是( )
| A. | 放在匀强磁场中的平面垂直于磁场方向时,穿过平面的磁通量最大 | |
| B. | 放在匀强磁场中的平面平行于磁场方向时,穿过平面的磁通量为零 | |
| C. | 穿过线圈的磁通量为零,则该处的磁感应强度一定为零 | |
| D. | 磁通量发生变化,不一定是磁场发生变化引起的 |

 如图所示K与虚线MN之间是加速电场.虚线MN与PQ之间是匀强电场,虚线PQ与荧光屏之间是匀强磁场,且MN、PQ与荧光屏三者互相平行.电场和磁场的方向如图所示.图中A点与O点的连线垂直于荧光屏.一带正电的粒子从A点离开加速电场,速度方向垂直于偏转电场方向射入偏转电场,在离开偏转电场后进入匀强磁场,最后恰好垂直地打在图中的荧光屏上.已知电场和磁场区域在竖直方向足够长,加速电场电压与偏转电场的场强关系为U=$\frac{Ed}{2}$,式中的d是偏转电场的宽度且为已知量,磁场的磁感应强度B与偏转电场的电场强度E和带电粒子离开加速电场的速度v0关系符合表达式v0=$\frac{E}{B}$,如图所示,试求:
如图所示K与虚线MN之间是加速电场.虚线MN与PQ之间是匀强电场,虚线PQ与荧光屏之间是匀强磁场,且MN、PQ与荧光屏三者互相平行.电场和磁场的方向如图所示.图中A点与O点的连线垂直于荧光屏.一带正电的粒子从A点离开加速电场,速度方向垂直于偏转电场方向射入偏转电场,在离开偏转电场后进入匀强磁场,最后恰好垂直地打在图中的荧光屏上.已知电场和磁场区域在竖直方向足够长,加速电场电压与偏转电场的场强关系为U=$\frac{Ed}{2}$,式中的d是偏转电场的宽度且为已知量,磁场的磁感应强度B与偏转电场的电场强度E和带电粒子离开加速电场的速度v0关系符合表达式v0=$\frac{E}{B}$,如图所示,试求: