题目内容
2.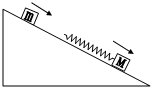 质量m和M的两木块分别以V1和V2的速度沿粗糙无限长的斜面匀速下滑.已知斜面固定,V1>V2.求两木块发生相互作用的过程中,轻质弹簧能达到的最大弹性势能.
质量m和M的两木块分别以V1和V2的速度沿粗糙无限长的斜面匀速下滑.已知斜面固定,V1>V2.求两木块发生相互作用的过程中,轻质弹簧能达到的最大弹性势能.
分析 两木块碰撞过程系统动量守恒,当两者速度相等时,弹簧的压缩量最大,弹簧弹性势能最大,应用动量守恒定律与能量守恒定律求出最大弹性势能.
解答 解:将两物块视为整体时,系统遵循动量守恒.且两物块速度相等时,轻质弹簧达到的弹性势能最大,
以平行与斜面向下为正方向,由动量守恒定律得:m1v1+m2v2=(m1+m2)v,
由能量守恒定律得:${E_{pm}}=\frac{1}{2}{m_1}v_1^2+\frac{1}{2}{m_2}v_2^2-\frac{1}{2}({m_1}+{m_2}){v^2}$,
联立方程得:${E_{pm}}=\frac{1}{2}{m_1}v_1^2+\frac{1}{2}{m_2}v_2^2-\frac{{{{({m_1}{v_1}+{m_2}{v_2})}^2}}}{{2({m_1}+{m_2})}}$;
答:轻质弹簧能达到的最大弹性势能为:$\frac{1}{2}$m1v12+$\frac{1}{2}$m2v22-$\frac{({m}_{1}{v}_{1}+{m}_{2}{v}_{2})^{2}}{2({m}_{1}+{m}_{2})}$.
点评 本题考查了求弹簧的弹性势能,分析清楚木块运动过程,应用动量守恒定律与能量守恒定律即可正确解题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.人站在台阶式自动扶梯上不动,随扶梯向上匀速运动,下列说法中错误的是( )
| A. | 重力对人做负功 | B. | 摩擦力对人做正功 | ||
| C. | 支持力对人做正功 | D. | 合力对人做功为零 |
10.水平桌面上重300N的物体,与桌面间的动摩擦因数是0.2,当用65N的水平力时,刚好能推动,当依次用15N、45NT和80N的水平力推此物体时,物体受到的摩擦力依次是( )
| A. | 15N、45N、80N | B. | 0N、60N、60N | C. | 15N、45N、65N | D. | 15N、45N、60N |
17. 内壁光滑的环形凹槽半径为R,固定在竖直平面内,一根长度为$\sqrt{2}$R的轻杆,一端固定有质量m的小球甲,另一端固定有质量为2m的小球乙.现将两小球放入凹槽内,初始时刻小球乙位于凹槽的最低点(如图所示),由静止释放后( )
内壁光滑的环形凹槽半径为R,固定在竖直平面内,一根长度为$\sqrt{2}$R的轻杆,一端固定有质量m的小球甲,另一端固定有质量为2m的小球乙.现将两小球放入凹槽内,初始时刻小球乙位于凹槽的最低点(如图所示),由静止释放后( )
 内壁光滑的环形凹槽半径为R,固定在竖直平面内,一根长度为$\sqrt{2}$R的轻杆,一端固定有质量m的小球甲,另一端固定有质量为2m的小球乙.现将两小球放入凹槽内,初始时刻小球乙位于凹槽的最低点(如图所示),由静止释放后( )
内壁光滑的环形凹槽半径为R,固定在竖直平面内,一根长度为$\sqrt{2}$R的轻杆,一端固定有质量m的小球甲,另一端固定有质量为2m的小球乙.现将两小球放入凹槽内,初始时刻小球乙位于凹槽的最低点(如图所示),由静止释放后( )| A. | 下滑过程中甲球减少的机械能总是等于乙球增加的机械能 | |
| B. | 下滑过程中甲球减少的重力势能总是等于乙球增加的重力势能 | |
| C. | 甲球沿凹槽下滑不可能到达槽的最低点 | |
| D. | 杆从右向左滑回时,乙球一定不能回到凹槽的最低点 |
7. 在如图所示的电路中,E、r为电源的电动势和内阻,R1和R3为定值电阻,R2为滑动变阻器.当R2的滑动触点在a端时合上开关S,此时三个电表A1、A2和V的示数分别为I1、I2和U.现将R2的滑动触点向b端移动,则三个电表示数的变化情况是( )
在如图所示的电路中,E、r为电源的电动势和内阻,R1和R3为定值电阻,R2为滑动变阻器.当R2的滑动触点在a端时合上开关S,此时三个电表A1、A2和V的示数分别为I1、I2和U.现将R2的滑动触点向b端移动,则三个电表示数的变化情况是( )
 在如图所示的电路中,E、r为电源的电动势和内阻,R1和R3为定值电阻,R2为滑动变阻器.当R2的滑动触点在a端时合上开关S,此时三个电表A1、A2和V的示数分别为I1、I2和U.现将R2的滑动触点向b端移动,则三个电表示数的变化情况是( )
在如图所示的电路中,E、r为电源的电动势和内阻,R1和R3为定值电阻,R2为滑动变阻器.当R2的滑动触点在a端时合上开关S,此时三个电表A1、A2和V的示数分别为I1、I2和U.现将R2的滑动触点向b端移动,则三个电表示数的变化情况是( )| A. | I1增大,I2不变,U增大 | B. | I1增大,I2减小,U增大 | ||
| C. | I1减小,I2增大,U减小 | D. | I1减小,I2不变,U减小 |
14.如图,开关S闭合,当滑片P左移时,关于两表的读数说法正确的是( )


| A. | 电流表变小,电压表变小 | B. | 电流表变大,电压表变大 | ||
| C. | 电流表变大,电压表变小 | D. | 电流表变小,电压表变大 |
11.一条船沿垂直河岸的方向航行,它在静水中航行速度大小一定,当船行驶到河中心时,河水流速突然增大,这使得该船( )
| A. | 渡河时间增大 | B. | 到达对岸时的速度不变 | ||
| C. | 渡河通过的路程增大 | D. | 渡河通过的路程比位移大 |
 如图甲所示,一个带负电的小物块正以速度v0沿斜面匀速下滑(设斜面足够长),若在运动过程中,加上一个垂直纸面向外的匀强磁场,则小物块运动v-t 的图象可能是图乙中的( )
如图甲所示,一个带负电的小物块正以速度v0沿斜面匀速下滑(设斜面足够长),若在运动过程中,加上一个垂直纸面向外的匀强磁场,则小物块运动v-t 的图象可能是图乙中的( )


