题目内容
15.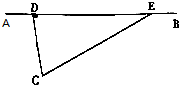 如图所示,AB、CD为互相垂直的丁字形公路,CE为通向公路AB的一条岔路,CD长sCD=300m,CE长sCE=500m,一逃犯骑着摩托车以v1=72km/h的速度正沿AB公路逃窜.当逃犯途经路口D处时,守候在C处的公安干警接到报告,立即分两路追捕,甲路沿CDB路径追捕逃犯,乙路沿CEB路径追捕逃犯,两路警车均以大小a=2.5m/s2的加速度匀加速度启动警车,当警车在匀加速运动的过程中速度大小达到vm=126km/h后,再以此速度匀速行驶,试问哪一路公安干警先追捕到逃犯,并求其追捕所用的时间.(不考虐警车转向速度大小的变化及时间)
如图所示,AB、CD为互相垂直的丁字形公路,CE为通向公路AB的一条岔路,CD长sCD=300m,CE长sCE=500m,一逃犯骑着摩托车以v1=72km/h的速度正沿AB公路逃窜.当逃犯途经路口D处时,守候在C处的公安干警接到报告,立即分两路追捕,甲路沿CDB路径追捕逃犯,乙路沿CEB路径追捕逃犯,两路警车均以大小a=2.5m/s2的加速度匀加速度启动警车,当警车在匀加速运动的过程中速度大小达到vm=126km/h后,再以此速度匀速行驶,试问哪一路公安干警先追捕到逃犯,并求其追捕所用的时间.(不考虐警车转向速度大小的变化及时间)
分析 先计算出警车到达最大速度所用的时间和距离,然后计算出逃犯在此时间内的位移,根据两者此时的距离差除以两者的速度差即可求出时间,也能求出此时的位置,第二问同理可得.
解答 解:(1)摩托车的速度为:v=20m/s,警车的最大速度为:vm≈35m/s.
警车达最大速度的时为:${t}_{1}=\frac{{v}_{m}}{a}$=$\frac{35}{2.5}$=14s,行驶的距离为:${s}_{1}=\frac{1}{2}a{{t}_{1}}^{2}$=245m,此时车还没有到达D点,也没有到达E点.
在t1时间内摩托车行驶的距离为:s1′=vt1=20×14=280m.
此时沿CD方向的警车与逃犯之间的距离:△s1=s1′+sCD-s1=280+300-245=335m
设需再经时间t2,警车才能追上摩托车,则有:t2=$\frac{△s}{{v}_{m}-v}$=$\frac{335}{35-20}$=22.33 s.
从而,截获逃犯总共所需时间为:t=t1+t2=14+22.33=36.33 s.
(2)由几何关系可知:DE=$\sqrt{{s}_{CE}^{2}-{s}_{CD}^{2}}=\sqrt{50{0}^{2}-30{0}^{2}}=400$m<s,
沿CE方向的车到达E点的时间为::${t}_{3}={t}_{1}+\frac{{s}_{CE}-{s}_{1}}{{v}_{m}}=14+\frac{500-245}{35}$=21.3s
此过程中逃犯的位移为:s1″=vt3=20×21.3=426m>DE
设需再经时间t4,警车才能追上摩托车,则有:t4=$\frac{s″-DE}{{v}_{m}-v}=\frac{426-400}{35-20}=1.73$s.
从而,截获逃犯总共所需时间为:t′=t3+t4=21.3+1.73=23.03 s<t.
答:沿CE方向的警车先追上.
点评 仔细分析警车和摩托车的运动过程,寻找两者在运动时间和路程上的联系,此类问题就不难得到顺利解决.

| A. | 向心加速度将变小 | B. | 线速度将变小 | ||
| C. | 周期将变大 | D. | 加速度将变大 |
 如图甲,一带电物块无初速度地放上皮带轮底端,皮带轮以恒定大小的速率沿顺时针传动,该装置处于垂直纸面向里的匀强磁场中,物块由底端E运动至皮带轮顶端F的过程中,其v-t图象如图乙所示,物块全程运动的时间为4.5s,关于带电物块及运动过程的说法正确的是( )
如图甲,一带电物块无初速度地放上皮带轮底端,皮带轮以恒定大小的速率沿顺时针传动,该装置处于垂直纸面向里的匀强磁场中,物块由底端E运动至皮带轮顶端F的过程中,其v-t图象如图乙所示,物块全程运动的时间为4.5s,关于带电物块及运动过程的说法正确的是( )| A. | 该物块可能带负电 | |
| B. | 若已知皮带的长度,可求出该过程中物块与皮带发生的相对位移 | |
| C. | 皮带轮的传动速度大小可能为2m/s | |
| D. | 在2s-4.5s内,物块与皮带仍可能有相对运动 |
 如图所示,图线a是线圈在匀强磁场中匀速转动时所产生正弦交流电的图象,当调整线圈转速后,所产生正弦交流电的图象如图线b所示,以下关于这两个正弦交流电的说法正确的是( )
如图所示,图线a是线圈在匀强磁场中匀速转动时所产生正弦交流电的图象,当调整线圈转速后,所产生正弦交流电的图象如图线b所示,以下关于这两个正弦交流电的说法正确的是( )| A. | 在图中t=0时刻穿过线圈的磁通量均为零 | |
| B. | 线圈先后两次转速之比为3:2 | |
| C. | 交流电a的瞬时值为u=10sintπt V | |
| D. | 交流电b的最大值为$\frac{20}{3}$V |
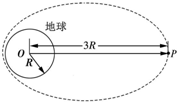 2015年12月10日,我国成功将中星1C卫星发射升空,卫星顺利进入预定转移轨道.如图所示是某卫星沿椭圆轨道绕地球运动的示意图,已知地球半径为R,地球表面的重力加速度为g,卫星远地点P距地心O的距离为3R.则( )
2015年12月10日,我国成功将中星1C卫星发射升空,卫星顺利进入预定转移轨道.如图所示是某卫星沿椭圆轨道绕地球运动的示意图,已知地球半径为R,地球表面的重力加速度为g,卫星远地点P距地心O的距离为3R.则( )| A. | 卫星在远地点的速度大于$\frac{\sqrt{3gR}}{3}$ | |
| B. | 卫星经过远地点时速度最小 | |
| C. | 卫星经过远地点时的加速度大小为$\frac{g}{9}$ | |
| D. | 卫星经过远地点时加速,卫星将不能再次经过远地点 |
| A. | 只有红色和绿色的双缝干涉,其他颜色的双缝干涉纹消失 | |
| B. | 任何颜色的双缝干涉条纹都不存在,但屏上仍有光亮 | |
| C. | 红色和绿色的双缝干涉条纹消失,其他颜色的双缝干涉条纹依然存在 | |
| D. | 屏上无任何光亮 |
 如图所示,质量为M=8kg的木板,放在水平地面上,木板向右运动的速度v0=5m/s时,在木板前端轻放一个大小不计,质量为m=2kg的小物块.木板与地面、物块与木板间的动摩擦因数均为μ=0.2,g=10m/s2,求:
如图所示,质量为M=8kg的木板,放在水平地面上,木板向右运动的速度v0=5m/s时,在木板前端轻放一个大小不计,质量为m=2kg的小物块.木板与地面、物块与木板间的动摩擦因数均为μ=0.2,g=10m/s2,求: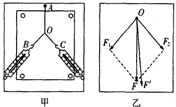 “验证力的平行四边形定则”的实验情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的图.
“验证力的平行四边形定则”的实验情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的图.