题目内容
20. 如图所示,一质量为M的斜面体静止在水平地面上,斜面体高度为h.质量为m的木块从顶端匀加速下滑到底端,速度大小由v1增大到v2,所用时间为t,木块下滑过程中斜面体始终保持静止.则在此过程中( )
如图所示,一质量为M的斜面体静止在水平地面上,斜面体高度为h.质量为m的木块从顶端匀加速下滑到底端,速度大小由v1增大到v2,所用时间为t,木块下滑过程中斜面体始终保持静止.则在此过程中( )| A. | 斜面体受水平地面的摩擦力为零 | |
| B. | 木块沿斜面下滑的距离为$\frac{{v}_{1}+{v}_{2}}{2}$t | |
| C. | 木块下滑过程中克服摩擦力所做的功为mgh-$\frac{1}{2}$mv22+$\frac{1}{2}$mv12 | |
| D. | 如果木块以初速度v2冲上斜面,它沿斜面上升到h高处时速度为v1 |
分析 应用整体法,由牛顿第二定律可分析地面对斜面体的摩擦力方向;由平均速度与时间的乘积可求得下滑距离;根据动能定理可求得克服摩擦力所做的功.根据下滑与上升加速度关系分析上升到h高处的速度.
解答 解:A、木块沿斜面匀加速下滑,加速度沿斜面向下,有水平向左的加速度,对整体分析可知,根据牛顿第二定律可知,整体在水平方向一定有水平向左的外力,所以地面与斜面间一定有静摩擦力;故A错误;
B、木块做匀加速运动,其下滑的平均速度为:$\overline{v}$=$\frac{{v}_{1}+{v}_{2}}{2}$,故下滑的距离为:x=$\overline{v}$t=$\frac{{v}_{1}+{v}_{2}}{2}$t;故B正确;
C、由动能定理可得:mgh-Wf=$\frac{1}{2}m{v}_{2}^{2}$-$\frac{1}{2}m{v}_{1}^{2}$;故木块下滑过程中克服摩擦力所做的功为:Wf=mgh+$\frac{1}{2}m{v}_{1}^{2}$-$\frac{1}{2}m{v}_{2}^{2}$;故C正确;
D、由于物体在斜面上受摩擦力,故沿斜面上升的加速度一定大于下滑的加速度,故上升h时的速度一定小于v1;故D错误;
故选:BC
点评 本题关键在于分析清楚运动过程并做好各过程的受力分析,应用能量守恒定律即可正确解题.

练习册系列答案
相关题目
10.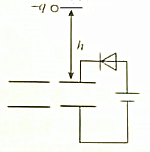 如图所示,平行板电容器水平放置,电源通过二极管给电容充电,上、下极板正中有一小孔,质量为m,电荷量为+q的小球从小孔正上方高h处由静止开始下落,穿过小孔到达下极板小孔处速度恰为零(空气阻力忽略不计,极板间电场可视为匀强电场)( )
如图所示,平行板电容器水平放置,电源通过二极管给电容充电,上、下极板正中有一小孔,质量为m,电荷量为+q的小球从小孔正上方高h处由静止开始下落,穿过小孔到达下极板小孔处速度恰为零(空气阻力忽略不计,极板间电场可视为匀强电场)( )
 如图所示,平行板电容器水平放置,电源通过二极管给电容充电,上、下极板正中有一小孔,质量为m,电荷量为+q的小球从小孔正上方高h处由静止开始下落,穿过小孔到达下极板小孔处速度恰为零(空气阻力忽略不计,极板间电场可视为匀强电场)( )
如图所示,平行板电容器水平放置,电源通过二极管给电容充电,上、下极板正中有一小孔,质量为m,电荷量为+q的小球从小孔正上方高h处由静止开始下落,穿过小孔到达下极板小孔处速度恰为零(空气阻力忽略不计,极板间电场可视为匀强电场)( )| A. | 若将上极板稍向上移动,则小球到达下极板小孔处速度恰为零 | |
| B. | 若将上极板稍向下移动,则小球到达下极板小孔处速度恰为零 | |
| C. | 若将下极板稍向上移动,则小球到达下极板小孔前速度就已为零 | |
| D. | 若将上极板稍向下移动,则小球到达下极板小孔处速度仍不为零 |
8. 如图所示,三维坐标系O-xyz的z轴方向竖直向上,所在空间存在沿y轴正方向的匀强电场.一质量为m、电荷量为+q的小球从z轴上的A点以速度v沿x轴正方向水平抛出,A点坐标为(0,0,L),重力加速度为g,场强E=$\frac{mg}{q}$.则下列说法中正确的是( )
如图所示,三维坐标系O-xyz的z轴方向竖直向上,所在空间存在沿y轴正方向的匀强电场.一质量为m、电荷量为+q的小球从z轴上的A点以速度v沿x轴正方向水平抛出,A点坐标为(0,0,L),重力加速度为g,场强E=$\frac{mg}{q}$.则下列说法中正确的是( )
 如图所示,三维坐标系O-xyz的z轴方向竖直向上,所在空间存在沿y轴正方向的匀强电场.一质量为m、电荷量为+q的小球从z轴上的A点以速度v沿x轴正方向水平抛出,A点坐标为(0,0,L),重力加速度为g,场强E=$\frac{mg}{q}$.则下列说法中正确的是( )
如图所示,三维坐标系O-xyz的z轴方向竖直向上,所在空间存在沿y轴正方向的匀强电场.一质量为m、电荷量为+q的小球从z轴上的A点以速度v沿x轴正方向水平抛出,A点坐标为(0,0,L),重力加速度为g,场强E=$\frac{mg}{q}$.则下列说法中正确的是( )| A. | 小球运动的轨迹为抛物线 | |
| B. | 小球在xOz平面内的分运动为非平抛运动 | |
| C. | 小球到达xOy平面时的速度大小为$\sqrt{{v^2}+2gL}$ | |
| D. | 小球的运动轨迹与xOy平面交点的坐标为(v$\sqrt{\frac{L}{g}}$,L,0) |
15. 如图所示,质量为M,内壁光滑的半球形绝缘容器静止在粗糙水平地面上,O为球心.两个完全相同的小球A、B质量均为m,带有同种电荷,带电量分别为qA、qB,A、B处于静止状态,两球与O的连线与水平面均成30°角,此时容器对A球的弹力为FN1.由于缓慢的漏电,A、B两球缓慢移动,经过时间t,A球与O的连线与水平面成60°角,此时A、B两球的带电量分别为qA′、qB′,容器对A球的弹力为FN2.关于此过程的说法正确的是( )
如图所示,质量为M,内壁光滑的半球形绝缘容器静止在粗糙水平地面上,O为球心.两个完全相同的小球A、B质量均为m,带有同种电荷,带电量分别为qA、qB,A、B处于静止状态,两球与O的连线与水平面均成30°角,此时容器对A球的弹力为FN1.由于缓慢的漏电,A、B两球缓慢移动,经过时间t,A球与O的连线与水平面成60°角,此时A、B两球的带电量分别为qA′、qB′,容器对A球的弹力为FN2.关于此过程的说法正确的是( )
 如图所示,质量为M,内壁光滑的半球形绝缘容器静止在粗糙水平地面上,O为球心.两个完全相同的小球A、B质量均为m,带有同种电荷,带电量分别为qA、qB,A、B处于静止状态,两球与O的连线与水平面均成30°角,此时容器对A球的弹力为FN1.由于缓慢的漏电,A、B两球缓慢移动,经过时间t,A球与O的连线与水平面成60°角,此时A、B两球的带电量分别为qA′、qB′,容器对A球的弹力为FN2.关于此过程的说法正确的是( )
如图所示,质量为M,内壁光滑的半球形绝缘容器静止在粗糙水平地面上,O为球心.两个完全相同的小球A、B质量均为m,带有同种电荷,带电量分别为qA、qB,A、B处于静止状态,两球与O的连线与水平面均成30°角,此时容器对A球的弹力为FN1.由于缓慢的漏电,A、B两球缓慢移动,经过时间t,A球与O的连线与水平面成60°角,此时A、B两球的带电量分别为qA′、qB′,容器对A球的弹力为FN2.关于此过程的说法正确的是( )| A. | 地面对容器有水平方向的摩擦力 | B. | FN1:FN2=1:$\sqrt{3}$ | ||
| C. | 地面对容器的弹力小于(M+2m)g | D. | (qAqB):(qA′qB′)=9:1 |
5. 如图所示,微粒A位于一定高度处,其质量m=1×10-4kg、带电荷量q=+1×10-6C,塑料长方体空心盒子B位于水平地面上,与地面间的动摩擦因数μ=0.1.B上表面的下方存在着竖直向上的匀强电场,场强大小E=2×103N/C,B上表面的上方存在着竖直向下的匀强电场,场强大小为$\frac{E}{2}$.B上表面开有一系列略大于A的小孔,孔间距满足一定的关系,使得A进出B的过程中始终不与B接触.当A以υ1=1m/s的速度从孔1竖直向下进入B的瞬间,B恰以υ2=0.6m/s的速度向右滑行.设B足够长、足够高且上表面的厚度忽略不计,取g=10m/s2,A恰能顺次从各个小孔进出B.则( )
如图所示,微粒A位于一定高度处,其质量m=1×10-4kg、带电荷量q=+1×10-6C,塑料长方体空心盒子B位于水平地面上,与地面间的动摩擦因数μ=0.1.B上表面的下方存在着竖直向上的匀强电场,场强大小E=2×103N/C,B上表面的上方存在着竖直向下的匀强电场,场强大小为$\frac{E}{2}$.B上表面开有一系列略大于A的小孔,孔间距满足一定的关系,使得A进出B的过程中始终不与B接触.当A以υ1=1m/s的速度从孔1竖直向下进入B的瞬间,B恰以υ2=0.6m/s的速度向右滑行.设B足够长、足够高且上表面的厚度忽略不计,取g=10m/s2,A恰能顺次从各个小孔进出B.则( )
 如图所示,微粒A位于一定高度处,其质量m=1×10-4kg、带电荷量q=+1×10-6C,塑料长方体空心盒子B位于水平地面上,与地面间的动摩擦因数μ=0.1.B上表面的下方存在着竖直向上的匀强电场,场强大小E=2×103N/C,B上表面的上方存在着竖直向下的匀强电场,场强大小为$\frac{E}{2}$.B上表面开有一系列略大于A的小孔,孔间距满足一定的关系,使得A进出B的过程中始终不与B接触.当A以υ1=1m/s的速度从孔1竖直向下进入B的瞬间,B恰以υ2=0.6m/s的速度向右滑行.设B足够长、足够高且上表面的厚度忽略不计,取g=10m/s2,A恰能顺次从各个小孔进出B.则( )
如图所示,微粒A位于一定高度处,其质量m=1×10-4kg、带电荷量q=+1×10-6C,塑料长方体空心盒子B位于水平地面上,与地面间的动摩擦因数μ=0.1.B上表面的下方存在着竖直向上的匀强电场,场强大小E=2×103N/C,B上表面的上方存在着竖直向下的匀强电场,场强大小为$\frac{E}{2}$.B上表面开有一系列略大于A的小孔,孔间距满足一定的关系,使得A进出B的过程中始终不与B接触.当A以υ1=1m/s的速度从孔1竖直向下进入B的瞬间,B恰以υ2=0.6m/s的速度向右滑行.设B足够长、足够高且上表面的厚度忽略不计,取g=10m/s2,A恰能顺次从各个小孔进出B.则( )| A. | 从A第一次进入B至B停止运动的过程中,B通过的总路程s为0.18m | |
| B. | 为了保证A始终不与B接触,B上的小孔个数至少有5个 | |
| C. | 为了保证A始终不与B接触,B上表面孔间距最小值为0.04m | |
| D. | 为了保证A始终不与B接触,B上表面孔间距最大值为0.1m |
 如图所示,在xOy平面内,0<x<2L的区域内有一方向竖直向上的匀强电场,2L<x<3L的区域内有一方向竖直向下的匀强电场,两电场强度大小相等.x>3L的区域内有一方向垂直于xOy平面向外的匀强磁场.某时刻,一带正电的粒子从坐标原点以沿x轴正方向的初速度v0进入电场;之后的另一时刻,一带负电粒子以同样的初速度从坐标原点进入电场.正、负粒子从电场进入磁场时速度方向与电场和磁场边界的夹角分别为60°和30°,两粒子在磁场中分别运动半周后在某点相遇.已经两粒子的重力以及两粒子之间的相互作用都可忽略不计,两粒子带电量大小相等.求:
如图所示,在xOy平面内,0<x<2L的区域内有一方向竖直向上的匀强电场,2L<x<3L的区域内有一方向竖直向下的匀强电场,两电场强度大小相等.x>3L的区域内有一方向垂直于xOy平面向外的匀强磁场.某时刻,一带正电的粒子从坐标原点以沿x轴正方向的初速度v0进入电场;之后的另一时刻,一带负电粒子以同样的初速度从坐标原点进入电场.正、负粒子从电场进入磁场时速度方向与电场和磁场边界的夹角分别为60°和30°,两粒子在磁场中分别运动半周后在某点相遇.已经两粒子的重力以及两粒子之间的相互作用都可忽略不计,两粒子带电量大小相等.求:

 如图所示,汽缸长为L=1m(汽缸的厚度可忽略不计),固定在水平面上,汽缸中有横截面积为S=100cm2的光滑活塞,活塞封闭了一定质量的理想气体,当温度为t=27℃,大气压为p0=1×105 Pa时,气柱长度为L0=0.4m.现缓慢拉动活塞,拉力最大值为F=500N,求:如果温度保持不变,能否将活塞从汽缸中拉出?
如图所示,汽缸长为L=1m(汽缸的厚度可忽略不计),固定在水平面上,汽缸中有横截面积为S=100cm2的光滑活塞,活塞封闭了一定质量的理想气体,当温度为t=27℃,大气压为p0=1×105 Pa时,气柱长度为L0=0.4m.现缓慢拉动活塞,拉力最大值为F=500N,求:如果温度保持不变,能否将活塞从汽缸中拉出?