��Ŀ����
12�� ��ͼ�����ô��ʹ�װ��ú���ʾ��ͼ�����д��ʹ���L=6m����Ǧ�=37�㣬ú���봫�ʹ���Ķ�Ħ��������=0.8�����ʹ��������ֺʹӶ��ְ뾶��ȣ��������ᶥ������ú���װ�������߶�H=1.8m������ú���������ĵ�ˮƽ����x=l.2m�����ڴ��ʹ����ɾ�ֹ�ͷ�һЩú�飨����Ϊ�ʵ㣩������m=5kg��ú���ڴ��ʹ������������͵��ߴ���Ҫʹú�����ֵ���ߵ�ˮƽ�׳������ڳ������ģ�ȡg=10m/s2��sin37��=0.6��cos37��=0.8����
��ͼ�����ô��ʹ�װ��ú���ʾ��ͼ�����д��ʹ���L=6m����Ǧ�=37�㣬ú���봫�ʹ���Ķ�Ħ��������=0.8�����ʹ��������ֺʹӶ��ְ뾶��ȣ��������ᶥ������ú���װ�������߶�H=1.8m������ú���������ĵ�ˮƽ����x=l.2m�����ڴ��ʹ����ɾ�ֹ�ͷ�һЩú�飨����Ϊ�ʵ㣩������m=5kg��ú���ڴ��ʹ������������͵��ߴ���Ҫʹú�����ֵ���ߵ�ˮƽ�׳������ڳ������ģ�ȡg=10m/s2��sin37��=0.6��cos37��=0.8������1��ú�����ֵ���ߵ�ˮƽ�׳�ʱ���ٶȣ�
��2�������ֺʹӶ��ֵİ뾶R��
��3���綯������ú������ĵĵ��ܣ�
���� ��1������ƽ���˶��Ĺ�����������ƽ���˶��ij��ٶȣ�
��2����Ϊƽ���˶��ij��ٶȵ��ڴ��ʹ������˶����ٶȣ����ú�鵽���ֵ���ߵ�ʱ���ֵ�ѹ��Ϊ�㣬����ţ�ٵڶ���������뾶�Ĵ�С��
��3������ţ�ٵڶ�����ú���ȼ���ֱ���˶��ļ��ٶȣ�ͨ���ٶ�ʱ�乫ʽ���ú���ڴ��ʹ����ɾ�ֹ��ʼ�������봫�ʹ��ٶ���ͬ��������ʱ�䣻���������غ㶨��������ʹ����ڴ���ú������ĵĵ��ܣ�
��� �⣺�� l ����ƽ���˶��Ĺ�ʽ���ã�
x=vt
H=$\frac{1}{2}$gt2
�������ݽ�ã�
v=x•$\sqrt{\frac{g}{2H}}$=1.2��$\sqrt{\frac{10}{2��1.8}}$=2m/s��
��2��Ҫʹú�����ֵ���ߵ���ƽ���˶�����ú�鵽���ֵ���ߵ�ʱ���ֵ�ѹ��Ϊ�㣬��ţ�ٵڶ����ɣ��ã�
mg=m$\frac{{v}^{2}}{R}$
�������ݣ��ã�
R=$\frac{{v}^{2}}{g}$=$\frac{4}{10}$=0.4m
��3����ţ�ٵڶ�����F=ma��
a=$\frac{F}{m}$=��gcos��-gsin��=0.8��10��0.8-10��0.6=0.4m/s2
��v=v0+at�ã����ٹ���ʱ��t=$\frac{v}{a}$=$\frac{2}{0.4}$=5s
����s=$\frac{1}{2}$at2 �ã�S=5m
S��=vt=2��5=10m
��S=S��-S=10-5=5m
�������غ�ã�
E=mgLsin37��+$\frac{1}{2}$mv2+f��S=5��10��6��0.6+$\frac{1}{2}$��5��4+0.8��50��0.8��5J=350J��
�𣺣�1�����ʹ������˶����ٶ�Ϊ2m/s��
��2���Ӷ��ֵİ뾶������0.4m��
��3�����ʹ����ڴ���ú�������350J���ܣ�
���� �����ۺϿ�����ƽ���˶���Բ���˶��Ĺ��ɣ�����ţ�ٵڶ����ɡ������غ㶨���Լ��˶�ѧ��ʽ��֪�����ٶ�����ϵ��ѧ���˶�ѧ��������

 ��ͼ��ʾ�����һͷP�ù⻬��̶�����ֱǽ���ϣ��˿���P��ת��������һͷO������������ǽ��A�㣬һ���屻������O�㣬��ǡ��ˮƽ�����ڽ�ǽ���������ҵ����ƣ�ͬʱ�ӳ�����ʹ���Ա���ˮƽ������������ѹ��������������������˵����ȷ���ǣ�������
��ͼ��ʾ�����һͷP�ù⻬��̶�����ֱǽ���ϣ��˿���P��ת��������һͷO������������ǽ��A�㣬һ���屻������O�㣬��ǡ��ˮƽ�����ڽ�ǽ���������ҵ����ƣ�ͬʱ�ӳ�����ʹ���Ա���ˮƽ������������ѹ��������������������˵����ȷ���ǣ�������| A�� | ���߾���С | B�� | ���߾����� | ||
| C�� | �����ѹ������������������С | D�� | �����ѹ����С���������������� |
| A�� | ��������� m��=$\frac{{g{R^2}}}{G}$ | |
| B�� | ̫��������m̫=$\frac{{4{��^2}L_2^3}}{GT_2^2}$ | |
| C�� | ���������m��=$\frac{{4{��^2}L_1^3}}{GT_1^2}$ | |
| D�� | �������������M��֪������������̫�����ܶ� |
 ��ͼ����ʾ��AB�ǵ糡�е�һ���糡�ߣ�������ijһ���ٶȴ�A����������ڵ糡����������ֱ�ߴ�A���˶���B�㣬����λ�õĵ������A��ľ���仯�Ĺ�����ͼ����ʾ��������˵����ȷ���ǣ�������
��ͼ����ʾ��AB�ǵ糡�е�һ���糡�ߣ�������ijһ���ٶȴ�A����������ڵ糡����������ֱ�ߴ�A���˶���B�㣬����λ�õĵ������A��ľ���仯�Ĺ�����ͼ����ʾ��������˵����ȷ���ǣ�������| A�� | A��B������ٶ�vA��vB | B�� | A��B����ĵ糡ǿ��EA��EB | ||
| C�� | A��B����ĵ���ϕA��ϕB | D�� | ������A��B����ĵ�����EpA��EpB |
| A�� | �����������������¶��йأ������������� | |
| B�� | ������¶�Խ�ߣ������з��������˶�Խ���� | |
| C�� | �����˶���Һ����ӵ��˶�����˵����������ͣϢ���������˶� | |
| D�� | ������ѹ��ʱ�����Ӽ���ڳ��������������� |
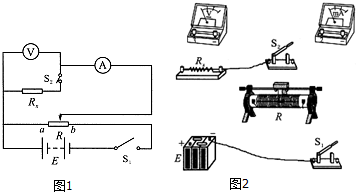
 ijͬѧ����ͼ��ʵ��װ�ò����������ٶȣ������������˶����������ܵĺ������ǡ�̽�����ܶ�����ʵ��Ҫ�����һ����Ҫ���⣮
ijͬѧ����ͼ��ʵ��װ�ò����������ٶȣ������������˶����������ܵĺ������ǡ�̽�����ܶ�����ʵ��Ҫ�����һ����Ҫ���⣮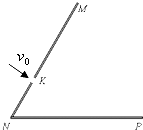 ��ͼ��ʾ����б����NM�ϵ�һ��С��K��NM��ˮƽ����NP��60��ǣ�K��N��ľ���$\overline{KN}$=a����������Ϊm�������Ϊq������������ɵ�����������ֱ����б����NM�����ٶ�v0�������룬�����������ܵ�������
��ͼ��ʾ����б����NM�ϵ�һ��С��K��NM��ˮƽ����NP��60��ǣ�K��N��ľ���$\overline{KN}$=a����������Ϊm�������Ϊq������������ɵ�����������ֱ����б����NM�����ٶ�v0�������룬�����������ܵ�������