题目内容
20.1798年英国物理学家卡文迪许测出万有引力常量G,因此卡文迪许被人们称为能称出地球质量的人.若已知万有引力常量G,地球表面处的重力加速度g,地球半径为R,地球上一个昼夜的时间为T0(地球自转周期),一年的时间T2(地球公转的周期),地球中心到月球中心的距离L1,月球绕地球的运动周期为T1,地球中心到太阳中心的距离为L2.则下列说法正确的是( )| A. | 地球的质量 m地=$\frac{{g{R^2}}}{G}$ | |
| B. | 太阳的质量m太=$\frac{{4{π^2}L_2^3}}{GT_2^2}$ | |
| C. | 月球的质量m月=$\frac{{4{π^2}L_1^3}}{GT_1^2}$ | |
| D. | 利用上面给出的M已知量可求月球、地球及太阳的密度 |
分析 根据万有引力等于重力求出地球的质量,根据地球绕太阳公转,靠万有引力提供向心力,求出太阳的质量.
解答 解:A、根据万有引力等于重力,有:G$\frac{{m}_{地}m}{{R}^{2}}$=mg.
则m地=$\frac{g{R}^{2}}{G}$.故A正确.
B、根据万有引力提供向心力有:G$\frac{{m}_{太}m}{{L}_{2}^{2}}$=mL2($\frac{2π}{{T}_{2}}$)2,解得m太=$\frac{4{π}^{2}{L}_{2}^{3}}{G{T}_{2}^{2}}$.故B正确.
C、因为月球的周期未知,无法求出月球的质量.故C错误.
D、月球的质量无法求出,则无法求出月球的密度.故D错误.
故选:AB.
点评 解决本题的关键掌握万有引力等于重力,以及万有引力提供向心力这两大理论,并能熟练运用.

练习册系列答案
相关题目
11.据每日邮报2014年4月18日报道,美国国家航空航天局(NASA)目前宣布首次在太阳系外发现“类地”行星Kepler-186f.假如宇航员乘坐宇宙飞船到达该行星,进行科学观测:该行星自转周期为T;宇航员在该行星“北极”距该行星地面附近h处自由释放一个小球(引力视为恒力),落地时间为t.已知该行星半径为R,万有引力常量为G,则下列说法正确的是( )
| A. | 该行星的第一宇宙速度为$\frac{πR}{T}$ | |
| B. | 宇宙飞船绕该星球做圆周运动的周期不小于πt$\sqrt{\frac{2R}{h}}$ | |
| C. | 该行星的平均密度为$\frac{3h}{2Gπ{t}^{2}}$ | |
| D. | 如果该行星存在一颗同步卫星,其距行星表面高度为$\root{3}{\frac{h{T}^{2}{R}^{2}}{2{π}^{2}{t}^{2}}}$ |
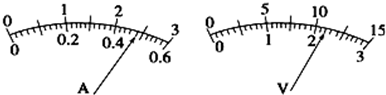
 如图所示,1、2、3、4为玻尔理论中氢原子最低的四个能级.一群氢原子在这些能级之间跃迁所辐射的光子最小波长等于多少?(普朗克常量h=6.62×10-34Js,计算结果保留一位有效数字).
如图所示,1、2、3、4为玻尔理论中氢原子最低的四个能级.一群氢原子在这些能级之间跃迁所辐射的光子最小波长等于多少?(普朗克常量h=6.62×10-34Js,计算结果保留一位有效数字).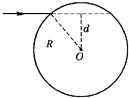 如图所示,一细束光线沿水平方向射入一圆形玻璃球.假设该光束射入玻璃球内经一次反射后从玻璃球中射出的光线与入射光线平行.
如图所示,一细束光线沿水平方向射入一圆形玻璃球.假设该光束射入玻璃球内经一次反射后从玻璃球中射出的光线与入射光线平行. 如图甲所示,空间存在B=0.5T,方向竖直向下的匀强磁场,MN、PQ是处于同一水平面内相互平行的粗糙长直导轨,间距L=0.2m,R是连接在导轨一端的电阻,ab是跨接在导轨上质量为m=0.1kg的导体棒.从零时刻开始,通过一小型电动机对ab棒施加一个牵引力F,方向水平向左,使其从静止开始沿导轨做加速运动,此过程中棒始终保持与导轨垂直且接触良好.图乙是棒的v-t图象,其中OA段是直线,AC是曲线,小型电动机在12s末达到额定功率P=4.5W,此后保持功率不变.除R外,其余部分电阻均不计,g=10m/s2.
如图甲所示,空间存在B=0.5T,方向竖直向下的匀强磁场,MN、PQ是处于同一水平面内相互平行的粗糙长直导轨,间距L=0.2m,R是连接在导轨一端的电阻,ab是跨接在导轨上质量为m=0.1kg的导体棒.从零时刻开始,通过一小型电动机对ab棒施加一个牵引力F,方向水平向左,使其从静止开始沿导轨做加速运动,此过程中棒始终保持与导轨垂直且接触良好.图乙是棒的v-t图象,其中OA段是直线,AC是曲线,小型电动机在12s末达到额定功率P=4.5W,此后保持功率不变.除R外,其余部分电阻均不计,g=10m/s2. 如图是利用传送带装运煤块的示意图.其中传送带长L=6m,倾角θ=37°,煤块与传送带间的动摩擦因数μ=0.8,传送带的主动轮和从动轮半径相等.主动轮轴顶端与运煤车底板间的竖起高度H=1.8m,与运煤车车厢中心的水平距离x=l.2m.现在传送带底端由静止释放一些煤块(可视为质点).质量m=5kg,煤块在传送带的作用下运送到高处.要使煤块在轮的最高点水平抛出并落在车厢中心.取g=10m/s2,sin37°=0.6,cos37°=0.8.求:
如图是利用传送带装运煤块的示意图.其中传送带长L=6m,倾角θ=37°,煤块与传送带间的动摩擦因数μ=0.8,传送带的主动轮和从动轮半径相等.主动轮轴顶端与运煤车底板间的竖起高度H=1.8m,与运煤车车厢中心的水平距离x=l.2m.现在传送带底端由静止释放一些煤块(可视为质点).质量m=5kg,煤块在传送带的作用下运送到高处.要使煤块在轮的最高点水平抛出并落在车厢中心.取g=10m/s2,sin37°=0.6,cos37°=0.8.求: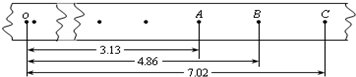
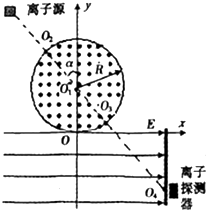 如图所示,圆形区域的匀强磁场垂直xoy平面向外,该圆形区域的圆心为O1,半径为R,并与x轴相切于原点O.现从离子源发出比荷为k(即电荷量与质量的比值)的正离子,沿直径O2O3射入,经磁场偏转后从O点垂直进入x轴下方的匀强电场,该电场的场强为E,方向沿x轴正方向,最后打在位于档板的o4位置的离子探测器上.不计粒子所受重力.已知O4点坐标为(2R,-R),且O1,O2,O3,O4在一条直线上.求:
如图所示,圆形区域的匀强磁场垂直xoy平面向外,该圆形区域的圆心为O1,半径为R,并与x轴相切于原点O.现从离子源发出比荷为k(即电荷量与质量的比值)的正离子,沿直径O2O3射入,经磁场偏转后从O点垂直进入x轴下方的匀强电场,该电场的场强为E,方向沿x轴正方向,最后打在位于档板的o4位置的离子探测器上.不计粒子所受重力.已知O4点坐标为(2R,-R),且O1,O2,O3,O4在一条直线上.求: