题目内容
7. 如图所示,一倾角为θ的光滑斜面固定在水平面上,斜面足够长,一质量为m的带电物体在沿斜面向上的匀强电场E作用下,从斜面底端由静止沿斜面向上做匀加速直线运动经过时间t,电势能减少了120J,此时撤去电场,之后物体又经过相同的时间t回到斜面底端,若以地面为零重力势能面,已知重力加速度为g,则下列说法正确的是( )
如图所示,一倾角为θ的光滑斜面固定在水平面上,斜面足够长,一质量为m的带电物体在沿斜面向上的匀强电场E作用下,从斜面底端由静止沿斜面向上做匀加速直线运动经过时间t,电势能减少了120J,此时撤去电场,之后物体又经过相同的时间t回到斜面底端,若以地面为零重力势能面,已知重力加速度为g,则下列说法正确的是( )| A. | 物体回到斜面底端的动能为60J | |
| B. | 物体带电荷量为q=$\frac{2mgsinθ}{E}$ | |
| C. | 撤去电场时,物体的重力势能是90J | |
| D. | 在前一个时间t内一定不会出现动能与重力势能相等的时刻 |
分析 对整个过程,根据动能定理求出物体回到出发点的动能.撤去电场后物体做匀减速直线运动,其位移与匀加速运动的位移大小相等、方向相反,根据运动学位移时间公式求出匀加速与匀减速加速度关系,由牛顿第二定律求出电荷量.根据电场力与mg的关系,由动能定理求解撤去电场时,物体的重力势能.
解答 解:A、在前t时间内,物体的电势能减少了120J,则电场力对物体做功为 WE=120J.对整个运动过程,根据动能定理得:WE=Ek-0,得到物体回到出发点时的动能为:
Ek=WF=120J.故A错误.
B、设前t时间内物体的加速度大小为a,后t时间内加速度大小为a′.由于匀加速运动与匀减速运动的位移大小相等、方向相反,则有:
$\frac{1}{2}a{t}^{2}$=-(at•t-$\frac{1}{2}a′{t}^{2}$),
解得 a′=3a
根据牛顿第二定律得:mgsinθ=ma′,解得 a′=gsinθ,可得 a=$\frac{1}{3}$gsinθ.再根据牛顿第二定律得:qE-mgsinθ=ma,解得 q=$\frac{4mgsinθ}{3E}$.故B错误.
C、匀加速运动过程:WF=qEs=120J,将 q=$\frac{4mgsinθ}{3E}$代入得到 $\frac{4}{3}$mgsinθ•s=120J,得到 mgsinθ•s=90J.则撤去力F时,物体的重力势能是Ep=mgsinθ•s=90J.故C正确.
D、撤去电场时物体的动能为 Ek=WF-mgsinθ•s=120J-90J=30J,撤去电场时,物体的重力势能是Ep=90J.可见此时物体的动能小于重力势能,撤去电场前物体的动能从零增大到30J,重力势能从零增大到90J,增大的快慢不同,所以在前一个时间t内一定不会出现动能与重力势能相等的时刻.故D正确.
故选:CD
点评 本题的关键要明确物体的运动过程,抓住两个过程的位移关系,要善于选择研究的过程,根据位移关系,由运动学公式求出加速度关系.

| A. | 汽车做减速运动,初速度大小为10m/s2 | |
| B. | 汽车做减速运动,加速度大小为5m/s2 | |
| C. | 汽车经过4s速度减小到零 | |
| D. | 汽车经过2s速度减小到零 |
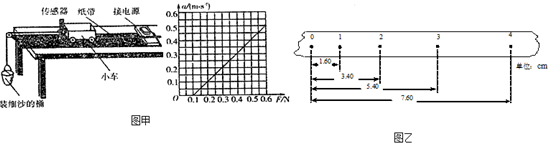
(1)对于本实验,以下说法中正确的是CD
A.砂和桶的总质量要远大于小车的总质量
B.每次改变小车质量后,需要重新平衡摩擦力
C.实验中也可不测加速度的具体数值,只要测出不同情况下加速度的比值就行了
D.若要验证“加速度与力的平方成正比”这一猜想,在作图线时最好以F2为横坐标
(2)某同学在接通电源进行实验之前,将实验器材组装如图1所示,下列对此同学操作的判断正确的是BCD

A.打点计时器不应固定在长木板的最右端,而应固定在靠近定滑轮的那端
B.打点计时器不应使用干电池,而应使用交流电源
C.不应将长木板水平放置,而应在右端垫起合适的高度,平衡摩擦力
D.小车初始位置不应离打点计时器太远,而应靠近打点计时器放置
(3)改正实验装置后,该同学顺利地完成了实验.在实验中保持拉力不变,得到了小车加速度随质量变化的一组数据,如下表所示:
| 实验次数 | 加速度 a/m•s-2 | 小车与砝码总质量 m/kg | 小车与砝码总质量的倒数 m-1/kg-1 |
| 1 | 0.32 | 0.20 | 5.0 |
| 2 | 0.25 | 0.25 | 4.0 |
| 3 | 0.21 | 0.30 | 3.3 |
| 4 | 0.18 | 0.35 | 2.9 |
| 5 | 0.16 | 0.40 | 2.5 |
(4)从图线可得出拉力大小为0.062N(结果保留两位有效数字).
(5)保持小车质量不变,改变砂和砂桶质量,某同学根据实验数据作出了加速度a随合力F的变化图线如图3所示.此图中直线发生明显弯曲的原因是随着F的增大,不再满足砂和桶的总质量远小于小车的总质量.
 如图所示,一个质量m的物体,从倾角为θ,高为h的斜面上端A点,由静止开始下滑,到B点时的速度为v,然后又在水平面上滑行s位移后停止在C点,物体从A点开始下滑到B点的过程中克服摩擦力所做的功为多少?物体与水平面间的动摩擦系数为多大?
如图所示,一个质量m的物体,从倾角为θ,高为h的斜面上端A点,由静止开始下滑,到B点时的速度为v,然后又在水平面上滑行s位移后停止在C点,物体从A点开始下滑到B点的过程中克服摩擦力所做的功为多少?物体与水平面间的动摩擦系数为多大? 如图所示,在竖直方向上A、B两物体通过劲度系数为k的轻质弹簧相连,A放在水平地面上;B、C两物体通过细线绕过轻质定滑轮相连,C放在固定的光滑斜面上.用手拿住C,使细线刚刚伸直但无拉力作用,并保证ab段的细线竖直、cd段的细线与斜面平行.已知A、B的质量均为m,斜面倾角为θ=37°,重力加速度为g,滑轮的质量和摩擦不计,开始时整个系统处于静止状态.C释放后沿斜面下滑,当A刚要离开地面时,B的速度最大,(sin 37°
如图所示,在竖直方向上A、B两物体通过劲度系数为k的轻质弹簧相连,A放在水平地面上;B、C两物体通过细线绕过轻质定滑轮相连,C放在固定的光滑斜面上.用手拿住C,使细线刚刚伸直但无拉力作用,并保证ab段的细线竖直、cd段的细线与斜面平行.已知A、B的质量均为m,斜面倾角为θ=37°,重力加速度为g,滑轮的质量和摩擦不计,开始时整个系统处于静止状态.C释放后沿斜面下滑,当A刚要离开地面时,B的速度最大,(sin 37°
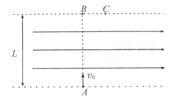 如图所示,在宽度为L的条形区域内有匀强电场,电场的方向平行于区域边界,一个带电粒子从下边界上的A点,以初速度v0沿垂直于电场的AB方向射入电场,从上边界的C点射出.已知粒子的重力不计,上边界上BC间距离为$\frac{1}{4}$L.
如图所示,在宽度为L的条形区域内有匀强电场,电场的方向平行于区域边界,一个带电粒子从下边界上的A点,以初速度v0沿垂直于电场的AB方向射入电场,从上边界的C点射出.已知粒子的重力不计,上边界上BC间距离为$\frac{1}{4}$L.