题目内容
9. 如图所示,在竖直方向上A、B两物体通过劲度系数为k的轻质弹簧相连,A放在水平地面上;B、C两物体通过细线绕过轻质定滑轮相连,C放在固定的光滑斜面上.用手拿住C,使细线刚刚伸直但无拉力作用,并保证ab段的细线竖直、cd段的细线与斜面平行.已知A、B的质量均为m,斜面倾角为θ=37°,重力加速度为g,滑轮的质量和摩擦不计,开始时整个系统处于静止状态.C释放后沿斜面下滑,当A刚要离开地面时,B的速度最大,(sin 37°
如图所示,在竖直方向上A、B两物体通过劲度系数为k的轻质弹簧相连,A放在水平地面上;B、C两物体通过细线绕过轻质定滑轮相连,C放在固定的光滑斜面上.用手拿住C,使细线刚刚伸直但无拉力作用,并保证ab段的细线竖直、cd段的细线与斜面平行.已知A、B的质量均为m,斜面倾角为θ=37°,重力加速度为g,滑轮的质量和摩擦不计,开始时整个系统处于静止状态.C释放后沿斜面下滑,当A刚要离开地面时,B的速度最大,(sin 37°=0.6,cos 37°=0.8)求:
(1)从开始到物体A刚要离开地面的过程中,物体C沿斜面下滑的距离;
(2)C的质量;
(3)A刚要离开地面时,C的动能.
分析 (1)物体C沿斜面下滑的距离等于B上升的高度,等于弹簧原来被压缩的长度再加上后来弹簧被拉长的长度,由胡克定律求解.
(2)物体A刚要离开地面时,分别以B和C为研究对象,利用牛顿第二定律列式,可求得C的质量.
(3)物体A刚好离开地面时,B、C两物体的速度相等,对BC整体,运用动能定理求解C的动能.
解答 解:(1)设开始时弹簧压缩的长度为xB,则有
kxB=mg
设当物体A刚要离开地面时,弹簧的伸长量为xA,则有
kxA=mg
当物体A刚要离开地面时,物体B上升的距离与物体C沿斜面下滑的距离相等,为:
h=xA+xB
解得:h=$\frac{2mg}{k}$.
(2)物体A刚要离开地面时,以B为研究对象,物体B受到重力mg、弹簧的弹力kxA、细线的拉力FT三个力的作用,设物体B的加速度为a,根据牛顿第二定律:
对B有:FT-mg-kxA=ma
对C有:mCgsin θ-FT=mCa
B获得最大速度时,有:a=0
解得:mC=$\frac{10m}{3}$.
(3)法一:由于xA=xB,弹簧处于压缩状态和伸长状态时的弹性势能相等,弹簧弹力做功为零,且物体A刚好离开地面时,B、C两物体的速度相等,设为v0,由动能定理得:
mCghsinθ-mgh+W弹=$\frac{1}{2}(m+{m}_{C}){v}_{0}^{2}$-0
其中,W弹=0
解得:v02=$\frac{12m{g}^{2}}{13k}$
所以 EkC=$\frac{1}{2}{m}_{c}{v}_{0}^{2}$=$\frac{20{m}^{2}{g}^{2}}{13k}$
法二:根据动能定理,
对C:mCghsinθ-Wr=EkC-0
对B:Wr-mgh+W弹=EkB-0
其中W弹=0
又EkC:EkB=10:3
解得:EkC=$\frac{20{m}^{2}{g}^{2}}{13k}$
答:
(1)从开始到物体A刚要离开地面的过程中,物体C沿斜面下滑的距离是$\frac{2mg}{k}$;
(2)C的质量是$\frac{10m}{3}$;
(3)A刚要离开地面时,C的动能是$\frac{20{m}^{2}{g}^{2}}{13k}$.
点评 本题关键是分析求出系统的运动状态,把握住弹簧的形变量与物体a下滑距离的关系,结合动能定理和胡克定律多次列式求解分析.

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案| A. | 不同的物体,若温度相等,则内能也相等 | |
| B. | 物体速度增大,则分子动能增大,内能也增大 | |
| C. | 冰熔解成水,温度不变,则内能也不变 | |
| D. | 对物体做功或向物体传热,都可能改变物体的内能 |
 如图所示,A带正电,B带负电,在库仑力作用下,它们以连线上某点O为圆心做匀速圆周运动,以下说法正确的是( )
如图所示,A带正电,B带负电,在库仑力作用下,它们以连线上某点O为圆心做匀速圆周运动,以下说法正确的是( )| A. | 它们所需向心力相等 | B. | 它们的运动半径与电荷量成反比 | ||
| C. | 它们做圆周运动的角速度相等 | D. | 它们的线速度与质量成反比 |
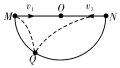 同时将两个小球以v1、v2的速度沿如图所示的方向抛出,发现两球刚好落在一个截面为半圆形的坑中同一点Q,已知∠MOQ=60°.忽略空气的阻力.则下列说法正确的是( )
同时将两个小球以v1、v2的速度沿如图所示的方向抛出,发现两球刚好落在一个截面为半圆形的坑中同一点Q,已知∠MOQ=60°.忽略空气的阻力.则下列说法正确的是( )| A. | $\frac{{v}_{1}}{{v}_{2}}$=$\frac{1}{3}$ | |
| B. | 仅增大v1,v2,则两球在坑中落点均在Q点右侧 | |
| C. | 两球的初速度无论怎样变化,只要落在坑中的同一点,v1+v2就为常数 | |
| D. | 若仅增大v1,则两球可在落在坑中前相遇 |
| A. | 电流I=$\frac{U}{R}$ | B. | 电场强度E=k$\frac{Q}{{r}^{2}}$ | C. | 导体的电阻R=ρ$\frac{l}{s}$ | D. | 电势φ=$\frac{W}{q}$ |
 如图所示,一倾角为θ的光滑斜面固定在水平面上,斜面足够长,一质量为m的带电物体在沿斜面向上的匀强电场E作用下,从斜面底端由静止沿斜面向上做匀加速直线运动经过时间t,电势能减少了120J,此时撤去电场,之后物体又经过相同的时间t回到斜面底端,若以地面为零重力势能面,已知重力加速度为g,则下列说法正确的是( )
如图所示,一倾角为θ的光滑斜面固定在水平面上,斜面足够长,一质量为m的带电物体在沿斜面向上的匀强电场E作用下,从斜面底端由静止沿斜面向上做匀加速直线运动经过时间t,电势能减少了120J,此时撤去电场,之后物体又经过相同的时间t回到斜面底端,若以地面为零重力势能面,已知重力加速度为g,则下列说法正确的是( )| A. | 物体回到斜面底端的动能为60J | |
| B. | 物体带电荷量为q=$\frac{2mgsinθ}{E}$ | |
| C. | 撤去电场时,物体的重力势能是90J | |
| D. | 在前一个时间t内一定不会出现动能与重力势能相等的时刻 |
 如图所示,水平传送带以一定速度匀速运动,将质量m=1kg的小物块轻轻放在传送带上的P点,物块运动到A点后被水平抛出,小物块恰好无碰撞地沿圆弧切线从B点进人竖直光滑圆弧轨道下滑.B,C为圆弧上的两点,其连线水平,已知圆弧半径R=1.0m对应圆心角θ=106°,A点距水平面的高度h=3.2m.小物块到达C点沿固定斜面向上滑动,2s后第二次经过D点,已知小物块与斜面间的动摩擦因数μ=$\frac{1}{3}$,重力速度g=10m/s2,sin53°=0.8,cos53°=0.6.求:
如图所示,水平传送带以一定速度匀速运动,将质量m=1kg的小物块轻轻放在传送带上的P点,物块运动到A点后被水平抛出,小物块恰好无碰撞地沿圆弧切线从B点进人竖直光滑圆弧轨道下滑.B,C为圆弧上的两点,其连线水平,已知圆弧半径R=1.0m对应圆心角θ=106°,A点距水平面的高度h=3.2m.小物块到达C点沿固定斜面向上滑动,2s后第二次经过D点,已知小物块与斜面间的动摩擦因数μ=$\frac{1}{3}$,重力速度g=10m/s2,sin53°=0.8,cos53°=0.6.求: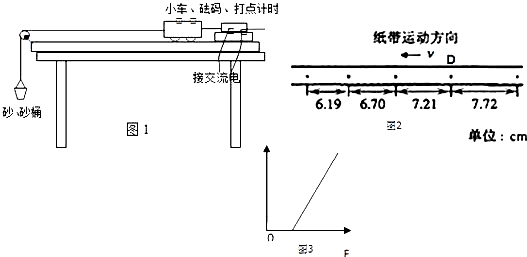
 如图所示是某同学做探究加速度与力、质量的关系实验时已接通电源正要释放纸带时的情况(小车上固定有力传感器测小车所受拉力,图中未画出)请你指出该同学的五个差错.
如图所示是某同学做探究加速度与力、质量的关系实验时已接通电源正要释放纸带时的情况(小车上固定有力传感器测小车所受拉力,图中未画出)请你指出该同学的五个差错.