题目内容
2.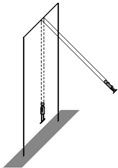 荡秋千是一项古老的运动,秋千是一块板用两根绳系在两个固定的悬点组成,设某人的质量为m,身高为H,站立时重心离脚底$\frac{H}{2}$,蹲下时重心离脚底$\frac{H}{4}$,绳子悬挂点到踏板的绳长为6H,绳子足够柔软且不可伸长,绳子和踏板的质量不计,人身体始终与绳子保持平行,重力加速度为g.
荡秋千是一项古老的运动,秋千是一块板用两根绳系在两个固定的悬点组成,设某人的质量为m,身高为H,站立时重心离脚底$\frac{H}{2}$,蹲下时重心离脚底$\frac{H}{4}$,绳子悬挂点到踏板的绳长为6H,绳子足够柔软且不可伸长,绳子和踏板的质量不计,人身体始终与绳子保持平行,重力加速度为g.(1)若该人在踏板上保持站式,由伙伴将其推至摆角θ0(单位:rad),由静止释放,忽略空气阻力,求摆至最低点时每根绳的拉力大小;
(2)若该人在踏板上保持站式,由伙伴将其推至摆角θ1 (单位:rad),由静止释放,摆至另一侧最大摆角为θ2(单位:rad),设空气阻力大小恒定,作用点距离脚底为$\frac{H}{3}$,求空气阻力的大小.
(3)若该人在踏板上采取如下步骤:当荡至最高处时,突然由蹲式迅速站起,而后缓缓蹲下,摆至另一侧最高处时已是蹲式,在该处又迅速站起,之后不断往复,可以荡起很高.用此法可以荡起的最大摆角为θm 弧度,假设人的“缓缓蹲下”这个动作不会导致系统机械能的损耗,而且空气阻力大小和作用点与第(2)问相同,试证明:$\frac{{θ}_{m}}{cos{θ}_{m}}$=$\frac{{θ}_{1}+{θ}_{2}}{44(cos{θ}_{2}-cos{θ}_{1})}$.
分析 (1)人在摆动过程中机械能守恒,根据机械能守恒定律列式求最低点速度,再根据重力和拉力的合力提供向心力列式求拉力;
(2)先计算出人从一侧最高点到另一侧最高点过程中机械能的减小量,然后根据大小恒定的变力做功的表达式W=FS计算出克服阻力做功等于阻力与路程的乘积;
(3)对人运动一个周期的过程进行分析,克服阻力做功等于阻力与路程的乘积,人做功补偿的机械能等于人站起而使重力势能增加的量,列方程求解.
解答 解:
(1)设荡至最低点时速度为v,则由机械能守恒定律有$\frac{1}{2}m{v}^{2}=mg(6H-\frac{H}{2})(1-cos{θ}_{0})$
设拉力为F,则由牛顿第二定律$F-mg=m\frac{{v}^{2}}{6H-\frac{H}{2}}$
求得F=3mg-2mgcosθ0
每根绳的拉力 $F'=\frac{1}{2}F=\frac{{3mg-2mgcos{θ_0}}}{2}$
(2)全程损耗的机械能为${△E}_{机}=mg(6H-\frac{H}{2})(cos{θ}_{2}-cos{θ}_{1})$
空气阻力做的功为${W}_{f}=-f(6H-\frac{H}{3})({θ}_{2}+{θ}_{1})$
由功能关系有Wf=△EK
求得 $f=\frac{{33(cos{θ_2}-cos{θ_1})}}{{34({θ_1}+{θ_2})}}mg$
(3)在一个周期内,通过“迅速站起”获得的机械能(重力势能)是
${△E}_{机}=2mg(\frac{H}{2}-\frac{H}{4})cos{θ}_{m}$
空气阻力做的功是${W}_{f}=-4f(6H-\frac{H}{3}){θ}_{m}$
由功能关系有Wf=△EK
求得:$\frac{{θ}_{m}}{cos{θ}_{m}}$=$\frac{{θ}_{1}+{θ}_{2}}{44(cos{θ}_{2}-cos{θ}_{1})}$,得证.
答:(1)摆至最低点时每根绳的拉力大小为$\frac{3mg-2mgcos{θ}_{0}}{2}$;
(2)空气阻力的大小为$\frac{33(cos{θ}_{2}-cos{θ}_{1})}{34({θ}_{1}+{θ}_{2})}mg$;
(3)证明如上.
点评 本题关键是根据功能关系列方程求解,要注意阻力做的功等于阻力与路程的乘积.

| A. | 两公式对一切情况都适用 | |
| B. | R=$\frac{U}{I}$仅适用于金属导体,R=ρ$\frac{l}{S}$适用于任何导体 | |
| C. | 导体的电阻R与U成正比,与I成反比 | |
| D. | 导体的电阻在温度一定时与导体长度成正比,与导体的横截面积成反比 |
| A. | 卫星的向心加速度大小为$\frac{GM}{R^2}$ | |
| B. | 卫星的线速度大小为$\sqrt{\frac{GM}{r}}$ | |
| C. | 若某一卫星加速,则其做圆周运动的半径将会变大 | |
| D. | 卫星上的物体处于完全失重的状态,不受地球的引力作用 |
 如图所示,在绝缘的水平面上等间距固定着三根相互平行的通电直导线a、b和c,各导线中的电流大小相同.其中a、c导线中的电流方向垂直纸面向外,b导线电流方向垂直纸面向里,每根导线都受到另外两根导线对它的安培力作用.则关于每根导线所受安培力的合力,以下说法正确的是( )
如图所示,在绝缘的水平面上等间距固定着三根相互平行的通电直导线a、b和c,各导线中的电流大小相同.其中a、c导线中的电流方向垂直纸面向外,b导线电流方向垂直纸面向里,每根导线都受到另外两根导线对它的安培力作用.则关于每根导线所受安培力的合力,以下说法正确的是( )| A. | 导线a所受合力方向水平向右 | B. | 导线c所受合力方向水平向右 | ||
| C. | 导线c所受合力方向水平向左 | D. | 导线b所受合力为零 |
| A. | 物体所受的重力一定竖直向下,物体的重心不一定在物体上 | |
| B. | 只有很小的物体才能视为质点,很大的物体不能视为质点 | |
| C. | 若两物体运动快慢相同,则两物体在相同时间内通过的位移一定相同 | |
| D. | “一江春水向东流”是以水为参考系来描述江水的运动 |
 圆形区域内有垂直于纸面的匀强磁场,三个质量和电荷量都相同的带电粒子a、b、c,以不同的速率沿着AO方向对准圆心O射入磁场,其运动轨迹如图所示.若带电粒子只受磁场力的作用,则下列说法正确的是( )
圆形区域内有垂直于纸面的匀强磁场,三个质量和电荷量都相同的带电粒子a、b、c,以不同的速率沿着AO方向对准圆心O射入磁场,其运动轨迹如图所示.若带电粒子只受磁场力的作用,则下列说法正确的是( )| A. | a粒子速率最大 | B. | c粒子速率最大 | ||
| C. | a粒子在磁场中运动的时间最短 | D. | 它们做圆周运动的周期Ta<Tb<Tc |
| A. | 700m/s | B. | 800m/s | C. | 900m/s | D. | 1000m/s |
 如图所示,倾角θ的斜面上有四条间距均为d的水平虚线,在Ⅰ、Ⅱ区存在匀强磁场,大小均为B,方向垂直于斜面向下.矩形线框ABCD的质量为m,长为2d,宽为L,电阻为R.将其从图示位置静止释放(AB边位于Ⅰ区上边界),CD边到达Ⅱ区上边界时,线框刚好做匀速直线运动.不计一切摩擦,重力加速度为g.求:
如图所示,倾角θ的斜面上有四条间距均为d的水平虚线,在Ⅰ、Ⅱ区存在匀强磁场,大小均为B,方向垂直于斜面向下.矩形线框ABCD的质量为m,长为2d,宽为L,电阻为R.将其从图示位置静止释放(AB边位于Ⅰ区上边界),CD边到达Ⅱ区上边界时,线框刚好做匀速直线运动.不计一切摩擦,重力加速度为g.求: