题目内容
9.某物理兴趣小组举行遥控赛车比赛,比赛路径如图所示.赛车从起点A出发,沿水平直线轨道运动L后,由B点进入半径为r的光滑竖直圆轨道,离开竖直圆轨道后继续在光滑平直轨道上运动到D点,并能越过以D点为圆心半径为R的壕沟.已知赛车质量m=0.2kg,通电后以额定功率P=1.5w工作,进入竖直轨道前受到阻力恒为0.3N,随后在运动中受到的阻力均可不计.图中AB间距L=10.00m,r=0.18m,R=4m,θ=60°.问: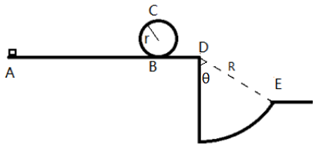
(1)要使赛车能够通过弧形壕沟,则赛车过D点时速度至少多少?
(2)要使赛车完成比赛,电动机至少工作多长时间?(取g=l0m/s2)
(3)若赛车刚好能过小圆轨道最高点,求赛车经过D点后第一次落地点与D点的水平距离.
分析 (1)根据类平抛运动的位移公式求解;
(2)对赛车从A到D应用动能定理,根据(1)中D点的速度求得时间;再根据赛车能通过C点,对赛车在C点应用牛顿第二定律求得速度,然后对A到C应用动能定理求得时间,然后取两时间中较大的那个最小值;
(3)根据赛车刚好能过小圆轨道最高点,应用牛顿第二定律求得在C点的速度,然后应用动能定理求得在D点的速度,即可根据平抛运动的位移公式求解.
解答 解:(1)小球离开D点后做平抛运动,那么,要使赛车能够通过弧形壕沟,竖直位移为h=Rcosθ,所以,平抛运动的时间为:
$t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2Rcos60°}{g}}=\sqrt{0.4}s$;
又有平抛运动的水平位移x≥Rsinθ,所以,赛车过D点时速度为:
${v}_{D}=\frac{x}{t}≥\frac{Rsinθ}{t}=\sqrt{30}m/d≈5.48m/s$;
(2)要使赛车完成比赛,那么赛车必能通过C点和D点,且在D点的速度为:${v}_{D}≥\sqrt{30}m/s$;
又有赛车运动过程,只有牵引力、阻力和重力作用,那么对赛车从A到D运用动能定理可得:$Pt-fL=\frac{1}{2}m{{v}_{D}}^{2}$
所以有:$t=\frac{fL+\frac{1}{2}m{{v}_{D}}^{2}}{P}≥4s$;
赛车要能通过C点,那么对赛车在C点应用牛顿第二定律可得:$\frac{m{{v}_{C}}^{2}}{r}≥mg$
那么由赛车只受牵引力、阻力和重力作用,对赛车从A到C应用动能定理可得:
$Pt′-fL-2mgr=\frac{1}{2}m{{v}_{C}}^{2}$
解得:$t′=\frac{\frac{1}{2}m{{v}_{C}}^{2}+2mgr+fL}{P}≥\frac{\frac{5}{2}mgr+fL}{P}=2.6s$;
故要使赛车完成比赛,电动机至少工作4s;
(3)若赛车刚好能过小圆轨道最高点,则对赛车在C点应用牛顿第二定律可得:$mg=\frac{m{v}_{C}{′}^{2}}{r}$;
那么,由赛车从C到D只有重力做功可,应用动能定理可得:$\frac{1}{2}m{v}_{D}{′}^{2}=\frac{1}{2}m{v}_{C}{′}^{2}+2mgr=\frac{5}{2}mgr$
解得:${v}_{D}′=\sqrt{5gr}=3m/s$;
那么由赛车经过D点后做平抛运动,vD′<vD,故赛车落在圆弧上;
由平抛运动位移公式可得:x=vD′t1,$y=\frac{1}{2}g{{t}_{1}}^{2}$
又有:x2+y2=R2;
解得:t1=0.8s;
所以,赛车经过D点后第一次落地点与D点的水平距离为:
x=vD′t1=2.4m;
答:(1)要使赛车能够通过弧形壕沟,则赛车过D点时速度至少为5.48m/s;
(2)要使赛车完成比赛,电动机至少工作4s;(取g=l0m/s2)
(3)若赛车刚好能过小圆轨道最高点,则赛车经过D点后第一次落地点与D点的水平距离为2.4m.
点评 经典力学问题,一般先对物体进行受力分析求得合外力,然后根据几何关系及牛顿第二定律得到运动状态;分析做功情况,即可由动能定理、能量守恒解决相关问题.

 阅读快车系列答案
阅读快车系列答案| A. | 平抛运动 | B. | 匀速直线运动 | C. | 匀速圆周运动 | D. | 匀加速直线运动 |
| A. | 甲乙两车在这段时间内的位移之比为4:3 | |
| B. | 甲车的功率增大到原来的2倍 | |
| C. | 甲乙两车在这段时间内克服阻力做功之比为12:11 | |
| D. | 甲乙两车在这段时间内牵引力做功之比为3:2 |
 如图所示,在固定的光滑水平杆上,质量为m的物体P用细线跨过光滑的滑轮OO′连接质量为2m的物体Q,用手托住Q使整个系统静止,此时轻绳刚好拉直,且AO=L,OB=h,AB<BO',重力加速度为g;释放Q,让二者开始运动,则下列说法正确的是 ( )
如图所示,在固定的光滑水平杆上,质量为m的物体P用细线跨过光滑的滑轮OO′连接质量为2m的物体Q,用手托住Q使整个系统静止,此时轻绳刚好拉直,且AO=L,OB=h,AB<BO',重力加速度为g;释放Q,让二者开始运动,则下列说法正确的是 ( )| A. | P物体从A点运动到O′的过程中,P、Q速度都在增大 | |
| B. | 在P物体从A滑到B的过程中,P的机械能增加、Q的机械能减小 | |
| C. | P运动的最大速度为$\sqrt{g(L-h)}$ | |
| D. | 当物体P到达B点时,物体Q减少的机械能为2mg(L-h) |
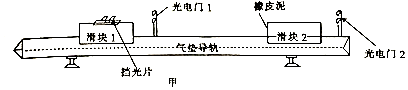
实验过程:
(1)调节气垫导轨水平,并使光电计时器系统正常工作.
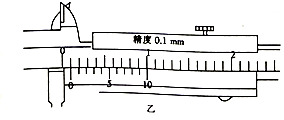
(2)在滑块1上装上挡光片,用游标卡尺测得其挡光宽度L如图乙所示,则L=1.0mm.
(3)在滑块2的碰撞端面粘上橡皮泥(或双面胶纸).
(4)用天平测出滑块1和滑块2的质量m1=0.4kg、m2=0.2kg.
(5)把滑块1和滑块2放在气垫导轨上,让滑块2处于静止状态(v2=0),用滑块1以初速度v1与之碰撞(这时光电计时器系统自动计算时间),撞后两者粘在一起,分别记下滑块1的挡光片碰前通过光电门1的挡光时间t1和碰后通过光电门2的挡光时间t2.
(6)先根据v=$\frac{L}{t}$计算滑块1碰撞前的速度v1及碰后两者的共同速度v;再计算两滑块碰撞前后的动量,并比较两滑块碰撞前后的动量的矢量和.
实验数据:(请在表格中的空白处填上相应的文字或数据)
| 次 数 | 滑块1 | 滑块2 | 碰前系统动量 (kg•m•s-1) | 碰后系统动量 kg•m•s-1 | |||
| v1/(m•s-1) | v/(m•s-1) | v2/(m•s-1) | v/(m•s-1) | m1v1 | m2v2 | (m1+m2)v | |
| 1 | 0.290 | 0.192 | 0 | 0.192 | ① | 0 | 0.115 |
| 2 | 0.453 | 0.296 | 0 | 0.296 | ② | 0 | ③ |
| 结论:④ | |||||||
| A. | 做曲线运动的物体所受的合力可能为零 | |
| B. | 做曲线运动的物体运动状态可能保持不变 | |
| C. | 做曲线运动的物体加速度可能不变 | |
| D. | 匀速圆周运动是一种匀变速运动 |
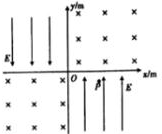 在xOy平面内存在着如图所示的匀强电场和匀强磁场,其中二、四象限内电场方向与y轴平行且大小相等、方向相反,一、三象限内磁场方向垂直xOy平面向里、磁感应强度大小B=0.2T,一带正电的粒子质量m=2×10-32kg、电荷量q=1×10-30C,从第四象限内的P(0.3m,-0.1m)点由静止释放,粒子垂直y轴方向进入第二象限,粒子重力不计,求:
在xOy平面内存在着如图所示的匀强电场和匀强磁场,其中二、四象限内电场方向与y轴平行且大小相等、方向相反,一、三象限内磁场方向垂直xOy平面向里、磁感应强度大小B=0.2T,一带正电的粒子质量m=2×10-32kg、电荷量q=1×10-30C,从第四象限内的P(0.3m,-0.1m)点由静止释放,粒子垂直y轴方向进入第二象限,粒子重力不计,求: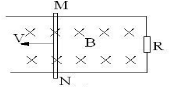 如图所示,在磁感应强度B=5T的匀强磁场中,垂直于磁场方向水平放置着两根相距为L=0.1m的平行光滑金属导轨,导轨的电阻忽略不计.在两根导轨的端点之间连接一阻值R=3Ω的电阻,导轨上跨放着一根电阻r=2Ω的金属棒MN,金属棒与导轨正交,当金属棒MN在外力作用下以速度v=4.0m/s向左做匀速运动时,试求:
如图所示,在磁感应强度B=5T的匀强磁场中,垂直于磁场方向水平放置着两根相距为L=0.1m的平行光滑金属导轨,导轨的电阻忽略不计.在两根导轨的端点之间连接一阻值R=3Ω的电阻,导轨上跨放着一根电阻r=2Ω的金属棒MN,金属棒与导轨正交,当金属棒MN在外力作用下以速度v=4.0m/s向左做匀速运动时,试求: