题目内容
7. 两根平行光滑金属导轨竖直放置,导轨间距为L,导轨电阻不计.导体棒AB和CD放置于导轨平面上且垂直于两条导轨,两导体棒质量均为m,长均为L,电阻均为R且与导轨接触良好.导体棒AB在宽度为a,磁感应强度B1随时间均匀增加的匀强磁场中,距磁场的下边界距离为b,如图所示.导体棒CD处于磁感应强度恒为B2的匀强磁场中恰好保持静止.导体棒AB在外力作用下始终保持静止,重力加速度为g.
两根平行光滑金属导轨竖直放置,导轨间距为L,导轨电阻不计.导体棒AB和CD放置于导轨平面上且垂直于两条导轨,两导体棒质量均为m,长均为L,电阻均为R且与导轨接触良好.导体棒AB在宽度为a,磁感应强度B1随时间均匀增加的匀强磁场中,距磁场的下边界距离为b,如图所示.导体棒CD处于磁感应强度恒为B2的匀强磁场中恰好保持静止.导体棒AB在外力作用下始终保持静止,重力加速度为g.(1)求通过导体棒CD的电流大小和方向;
(2)导体棒AB所在处磁场的磁感应强度的变化率$\frac{△{B}_{1}}{△t}$.
分析 (1)导体棒CD静止,处于平衡状态,应用平衡条件可以求出感应电流大小,应用左手定则可以判断出电流方向.
(2)应用欧姆定律求出感应电动势大小,然后应用法拉第电磁感应定律求出磁感应强度的变化率.
解答 解:(1)导体棒CD静止处于平衡状态,由平衡条件可知,
导体棒所受安培力方向竖直向上,由左手定则可知,电流从D流向C;
导体棒受到的安培力:F=BIL,
由平衡条件得:mg=B2L,
电流:I=$\frac{mg}{{B}_{2}L}$;
(2)由欧姆定律可知,
感应电动势:E=I(R+R)=$\frac{2mgR}{{B}_{2}L}$,
由法拉第电磁感应定律得:
E=$\frac{△Φ}{△t}$=$\frac{△{B}_{1}}{△t}$S=$\frac{△{B}_{1}}{△t}$Lb,
则:$\frac{△{B}_{1}}{△t}$Lb=$\frac{2mgR}{{B}_{2}L}$,
解得:$\frac{△{B}_{1}}{△t}$=$\frac{2mgR}{b{B}_{2}{L}^{2}}$;
答:(1)通过导体棒CD的电流大小为$\frac{mg}{{B}_{2}L}$,方向:由D流向C
(2)导体棒AB所在处磁场的磁感应强度的变化率$\frac{△{B}_{1}}{△t}$为$\frac{2mgR}{b{B}_{2}{L}^{2}}$.
点评 本题考查了求感应电流大小与方向,磁感应强度的变化率,分析清楚题意,应用平衡条件、法拉第电磁感应定律、欧姆定律可以解题.

练习册系列答案
相关题目
2.(多选)人握住旗杆匀速上爬,则下列说法正确的是( )
| A. | 人受到的摩擦力的方向是沿杆向下的 | |
| B. | 人受到的摩擦力的方向是沿杆向上的 | |
| C. | 人握旗杆用力越大,人受的摩擦力也越大 | |
| D. | 人握旗杆用力越大,并不会使人受的摩擦力增大 |
12.质量相同的氢气和氧气,温度相同,如果气体分子势能忽略不计,则( )
| A. | 氧气的内能较大 | |
| B. | 氢气的内能较大 | |
| C. | 氢气分子的平均动能和氧气分子的平均动能相同 | |
| D. | 氢气分子的平均速率和氧气分子的平均速率相同 |
13.在地面附近有一高速飞过的火箭,关于地面上的人和火箭中的人观察到的现象,以下说法正确的是( )
| A. | 地面上的人观察到火箭变短了,火箭上的时间进程变快了 | |
| B. | 地面上的人观察到火箭变短了,火箭上的时间进程变慢了 | |
| C. | 火箭上的人观察到地面上的物体长度和时间进程均无变化 | |
| D. | 火箭上的人观察到地面上的物体长度变小,时间进程变慢了 |
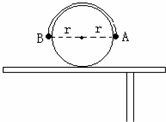 一个光滑的圆柱体固定在桌面上,圆柱体的半径为r,质量分别为mA和mB的两个小球A和B(都可看作质点,且mA>mB),用一根细线相连接,细线的长度恰好等于圆柱体的半个周长,开始时使两小球位于同一水平面上,如图所示,无初速地释放,A球向下运动,B球沿圆柱面运动.求
一个光滑的圆柱体固定在桌面上,圆柱体的半径为r,质量分别为mA和mB的两个小球A和B(都可看作质点,且mA>mB),用一根细线相连接,细线的长度恰好等于圆柱体的半个周长,开始时使两小球位于同一水平面上,如图所示,无初速地释放,A球向下运动,B球沿圆柱面运动.求 图中工人在推动一台割草机,施加的力大小为100N,方向与水平地面成30°斜向下.g=10m/s2
图中工人在推动一台割草机,施加的力大小为100N,方向与水平地面成30°斜向下.g=10m/s2