题目内容
19. 如图所示,固定于同一竖直线上的AB是两个带等量异种电荷的点电荷,电荷分别为+Q和-Q,AB相距为2d,MN是竖直放置的光滑绝缘细杆,另有一个穿细杆带电小球p,质量为m电荷量为+q(视为电荷不影响电场的分布)现将小球p从与点电荷A等高的C处由静止开始释放,小球p向下运动到距C点距d时,速度为v0;已知MN与AB之间的距离为d,静电力常数为k,重力加速度为g,求:
如图所示,固定于同一竖直线上的AB是两个带等量异种电荷的点电荷,电荷分别为+Q和-Q,AB相距为2d,MN是竖直放置的光滑绝缘细杆,另有一个穿细杆带电小球p,质量为m电荷量为+q(视为电荷不影响电场的分布)现将小球p从与点电荷A等高的C处由静止开始释放,小球p向下运动到距C点距d时,速度为v0;已知MN与AB之间的距离为d,静电力常数为k,重力加速度为g,求:(1)O点处的电场强度E的大小;
(2)CO间的电势差UCO;
(3)小球P经过与点电荷等高的D点时的速度.
分析 (1)根据库仑定律求出小球在O点所受的电场力,再根据电场强度的定义式E=$\frac{F}{q}$求出电场强度的大小.
(2)对小球从C到O的过程,运用动能定理,求出C、O间的电势差UCO.
(3)小球由C点到O点与从O点到D点,电场力的功相同,对从C点到D点过程,根据动能定理求小球P经过与点电荷等高的D点时的速度.
解答 解:(1)小球在O点时受力如图所示;
由库仑定律得:F1=F2=k$\frac{Qq}{(\sqrt{2}d)^{2}}$
点电荷在O点所受的电场力为:F=$\sqrt{2}{F}_{1}$=$\frac{\sqrt{2}kQq}{2{d}^{2}}$
所以O点处的电场强度E=$\frac{F}{q}$=$\frac{\sqrt{2}kQ}{2{d}^{2}}$.
(2)小球P由C点运动到O点时,由动能定理,得:
mgd+qUCO=$\frac{1}{2}$mv02-0
解得 UCO=$\frac{m{v}^{2}-2mgd}{2q}$
(3)小球P由C点到O点与从O点到D点,电场力的功相同,则从C点到D点,根据动能定理得:
mg•2d+2qUCD=$\frac{1}{2}$mv2
则 v=$\sqrt{2}{v}_{0}$.
答:(1)O点处的电场强度E的大小是$\frac{\sqrt{2}kQ}{2{d}^{2}}$;
(2)CO间的电势差UCO是$\frac{m{v}^{2}-2mgd}{2q}$;
(3)小球P经过与点电荷等高的D点时的速度是$\sqrt{2}{v}_{0}$.
点评 本题的关键要正确分析小球的受力情况,明确各个力做功关系,要知道O点的场强实际上是两点电荷在O点产生场强的合场强.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
10.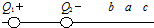 如图所示,Q1、Q2为两个被固定的正负点电荷,在它们的连线的延长线上的a点,电场强度恰好为零,现把另一正电荷q从b点移到c点,该电荷的电势能将( )
如图所示,Q1、Q2为两个被固定的正负点电荷,在它们的连线的延长线上的a点,电场强度恰好为零,现把另一正电荷q从b点移到c点,该电荷的电势能将( )
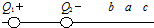 如图所示,Q1、Q2为两个被固定的正负点电荷,在它们的连线的延长线上的a点,电场强度恰好为零,现把另一正电荷q从b点移到c点,该电荷的电势能将( )
如图所示,Q1、Q2为两个被固定的正负点电荷,在它们的连线的延长线上的a点,电场强度恰好为零,现把另一正电荷q从b点移到c点,该电荷的电势能将( )| A. | 不断增大 | B. | 不断减少 | C. | 先增大后减少 | D. | 先减少后增大 |
7. 在正电荷形成的电场中,一带电粒子仅在电场力的作 用下的运动轨迹如图所示的abcd曲线,下列判断正确的是( )
在正电荷形成的电场中,一带电粒子仅在电场力的作 用下的运动轨迹如图所示的abcd曲线,下列判断正确的是( )
 在正电荷形成的电场中,一带电粒子仅在电场力的作 用下的运动轨迹如图所示的abcd曲线,下列判断正确的是( )
在正电荷形成的电场中,一带电粒子仅在电场力的作 用下的运动轨迹如图所示的abcd曲线,下列判断正确的是( )| A. | 粒子带负电 | B. | 粒子带正电 | ||
| C. | 电场力先做正功后做负功 | D. | 电场力先做负功后做正功 |
14. 如图所示,匀强电场场强为1×103 N/C,ab=dc=4cm,bc=ad=3cm,则下述计算结果正确的是( )
如图所示,匀强电场场强为1×103 N/C,ab=dc=4cm,bc=ad=3cm,则下述计算结果正确的是( )
 如图所示,匀强电场场强为1×103 N/C,ab=dc=4cm,bc=ad=3cm,则下述计算结果正确的是( )
如图所示,匀强电场场强为1×103 N/C,ab=dc=4cm,bc=ad=3cm,则下述计算结果正确的是( )| A. | ab之间的电势差为4000 V | |
| B. | ac之间的电势差为50 V | |
| C. | 将q=-5×10-3 C的点电荷沿矩形路径abcda移动一周,静电力做功为零 | |
| D. | 将q=-5×10-3 C的点电荷沿abc或adc从a移到c静电力做功都是-0.25 J |
11.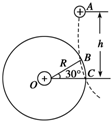 如图所示,在O点放置一个正点电荷,在过O点的竖直平面内的A点,自由释放一个带正电的小球,小球的质量为m、电荷量为q.小球落下的轨迹如图中虚线所示,它与以O为圆心、R为半径的圆(图中实线表示)相交于B、C两点,O、C在同一水平线上,∠BOC=30°,A距离OC的竖直高度为h.若小球通过B点的速度为v,则下列说法正确的是( )
如图所示,在O点放置一个正点电荷,在过O点的竖直平面内的A点,自由释放一个带正电的小球,小球的质量为m、电荷量为q.小球落下的轨迹如图中虚线所示,它与以O为圆心、R为半径的圆(图中实线表示)相交于B、C两点,O、C在同一水平线上,∠BOC=30°,A距离OC的竖直高度为h.若小球通过B点的速度为v,则下列说法正确的是( )
 如图所示,在O点放置一个正点电荷,在过O点的竖直平面内的A点,自由释放一个带正电的小球,小球的质量为m、电荷量为q.小球落下的轨迹如图中虚线所示,它与以O为圆心、R为半径的圆(图中实线表示)相交于B、C两点,O、C在同一水平线上,∠BOC=30°,A距离OC的竖直高度为h.若小球通过B点的速度为v,则下列说法正确的是( )
如图所示,在O点放置一个正点电荷,在过O点的竖直平面内的A点,自由释放一个带正电的小球,小球的质量为m、电荷量为q.小球落下的轨迹如图中虚线所示,它与以O为圆心、R为半径的圆(图中实线表示)相交于B、C两点,O、C在同一水平线上,∠BOC=30°,A距离OC的竖直高度为h.若小球通过B点的速度为v,则下列说法正确的是( )| A. | 小球通过C点的速度大小是$\sqrt{2gh}$ | |
| B. | 小球通过C点的速度大小是$\sqrt{{v}^{2}+gR}$ | |
| C. | 小球由A到C机械能的损失是mg(h-$\frac{R}{2}$)-$\frac{1}{2}$mv2 | |
| D. | 小球由A到C电场力做功是$\frac{1}{2}$mv2-mgh |
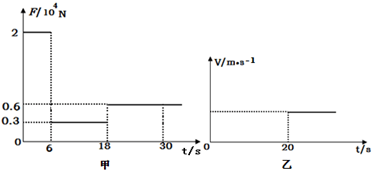
9. 如图所示,倾角为α的光滑导轨上端接入一定值电阻,I和Ⅱ是边长都为L的两正方形磁场区域,其区域内的磁场方向都垂直于导轨平面向上,区域Ⅰ中磁场的磁感应强度为B1,恒定不变,区域Ⅱ中磁场随时间按B2=kt变化,一质量为m、电阻为r的金属杆穿过区域Ⅰ垂直地跨放在两导轨上,并恰能保持静止,则下列说法正确的是( )
如图所示,倾角为α的光滑导轨上端接入一定值电阻,I和Ⅱ是边长都为L的两正方形磁场区域,其区域内的磁场方向都垂直于导轨平面向上,区域Ⅰ中磁场的磁感应强度为B1,恒定不变,区域Ⅱ中磁场随时间按B2=kt变化,一质量为m、电阻为r的金属杆穿过区域Ⅰ垂直地跨放在两导轨上,并恰能保持静止,则下列说法正确的是( )
 如图所示,倾角为α的光滑导轨上端接入一定值电阻,I和Ⅱ是边长都为L的两正方形磁场区域,其区域内的磁场方向都垂直于导轨平面向上,区域Ⅰ中磁场的磁感应强度为B1,恒定不变,区域Ⅱ中磁场随时间按B2=kt变化,一质量为m、电阻为r的金属杆穿过区域Ⅰ垂直地跨放在两导轨上,并恰能保持静止,则下列说法正确的是( )
如图所示,倾角为α的光滑导轨上端接入一定值电阻,I和Ⅱ是边长都为L的两正方形磁场区域,其区域内的磁场方向都垂直于导轨平面向上,区域Ⅰ中磁场的磁感应强度为B1,恒定不变,区域Ⅱ中磁场随时间按B2=kt变化,一质量为m、电阻为r的金属杆穿过区域Ⅰ垂直地跨放在两导轨上,并恰能保持静止,则下列说法正确的是( )| A. | 通过金属杆的电流大小为$\frac{mgsinα}{{B}_{1}L}$ | |
| B. | 通过金属杆的电流方向是从a到b | |
| C. | 定值电阻的阻值为$\frac{k{B}_{1}{L}^{3}}{mgsinα}$-r | |
| D. | 定值电阻的阻值为$\frac{k{B}_{1}{L}^{3}}{mgsinα}$ |
 匀强电场中的三点A、B、C是一个三角形的三个顶点,AB的长度为1m,D为AB的中点,如图所示.已知电场线的方向平行于△ABC所在平面,A、B、C三点的电势分别为14V、6V和2V.作图求电场强度的方向.
匀强电场中的三点A、B、C是一个三角形的三个顶点,AB的长度为1m,D为AB的中点,如图所示.已知电场线的方向平行于△ABC所在平面,A、B、C三点的电势分别为14V、6V和2V.作图求电场强度的方向.