题目内容
17. 质量均为M的物体A和B相距L,在光滑水平面上以相同的速度v向前匀速运动,某时刻将质量为$\frac{M}{2}$的物体C轻轻地放在B内,而后B、C一起向前运动,求:
质量均为M的物体A和B相距L,在光滑水平面上以相同的速度v向前匀速运动,某时刻将质量为$\frac{M}{2}$的物体C轻轻地放在B内,而后B、C一起向前运动,求:(1)经多长时间A与B相遇;
(2)将C放入B后,BC系统损失的机械能是多少.
分析 ①物体C轻轻地放在B内,两者组成的系统水平方向动量守恒,由动量守恒定律求出共同速度.之后两者一起向右匀速运动,B的速度减小了,A经过一段时间追上B,位移时间公式和位移关系求时间;
②将C放入B后,根据能量守恒定律求C系统损失的机械能.
解答 解:①B、C系统水平方向动量守恒,取向右为正方向,由动量守恒定律有
Mv=(M+$\frac{M}{2}$)vBC;
解得 vBC=$\frac{2}{3}$v
设经t时间A与B相遇,则有
L=(v-vBC)t
解得 t=$\frac{3L}{v}$
②将C放入B后,C系统损失的机械能△E=$\frac{1}{2}$Mv2-$\frac{1}{2}$(M+$\frac{M}{2}$)vBC2;
解得△E=$\frac{1}{6}M{v}^{2}$
答:
①经$\frac{3L}{v}$时间A与B相遇;
②将C放入B后,C系统损失的机械能是$\frac{1}{6}M{v}^{2}$.
点评 本题要注意在C放入B中的过程中,只遵守水平方向动量守恒,而系统的总动量并不守恒,根据水平方向动量守恒求共同速度.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
7. 如图所示,一束复色光从圆柱形玻璃砖的侧面A点,以45°的入射角射入玻璃砖,结果从玻璃砖的侧面B点和C点各射出一束单色光a和 b,则下列说法正确的是( )
如图所示,一束复色光从圆柱形玻璃砖的侧面A点,以45°的入射角射入玻璃砖,结果从玻璃砖的侧面B点和C点各射出一束单色光a和 b,则下列说法正确的是( )
 如图所示,一束复色光从圆柱形玻璃砖的侧面A点,以45°的入射角射入玻璃砖,结果从玻璃砖的侧面B点和C点各射出一束单色光a和 b,则下列说法正确的是( )
如图所示,一束复色光从圆柱形玻璃砖的侧面A点,以45°的入射角射入玻璃砖,结果从玻璃砖的侧面B点和C点各射出一束单色光a和 b,则下列说法正确的是( )| A. | 若单色光a是黄光,单色光b则可能是紫光 | |
| B. | 经同一双缝干涉实验装置,a光形成的条纹间距比b光形成的条纹间距小 | |
| C. | 单色光a在玻璃中从A到B的传播时间比单色光b从A到C的传播时间长 | |
| D. | 逐渐增大复色光在A点的入射角,则b光束先于a光束在玻璃砖中发生全反射 |
8. 如图D是一只理想二极管,PQ为一平行板电容器,其两极板接在一个恒压电源上,Q板接地.两地间有x、y两点,其中y点处有一带电微粒处于静止状态,若将极板Q向下由图中实线位置移至虚线位置,则( )
如图D是一只理想二极管,PQ为一平行板电容器,其两极板接在一个恒压电源上,Q板接地.两地间有x、y两点,其中y点处有一带电微粒处于静止状态,若将极板Q向下由图中实线位置移至虚线位置,则( )
 如图D是一只理想二极管,PQ为一平行板电容器,其两极板接在一个恒压电源上,Q板接地.两地间有x、y两点,其中y点处有一带电微粒处于静止状态,若将极板Q向下由图中实线位置移至虚线位置,则( )
如图D是一只理想二极管,PQ为一平行板电容器,其两极板接在一个恒压电源上,Q板接地.两地间有x、y两点,其中y点处有一带电微粒处于静止状态,若将极板Q向下由图中实线位置移至虚线位置,则( )| A. | x、y两点间电势差变小 | B. | x点处的电势降低 | ||
| C. | y点处带电微粒仍处于静止状态 | D. | Q极板所带的电荷量不变 |
12. 如图所示,从斜面上某一位置先后由静止释放四个小球.相邻两小球释放的时间间隔为0.1s,某时刻拍下小球所处位置的照片,测出xAB=5cm,xBC=10cm,xCD=15 cm.则( )
如图所示,从斜面上某一位置先后由静止释放四个小球.相邻两小球释放的时间间隔为0.1s,某时刻拍下小球所处位置的照片,测出xAB=5cm,xBC=10cm,xCD=15 cm.则( )
 如图所示,从斜面上某一位置先后由静止释放四个小球.相邻两小球释放的时间间隔为0.1s,某时刻拍下小球所处位置的照片,测出xAB=5cm,xBC=10cm,xCD=15 cm.则( )
如图所示,从斜面上某一位置先后由静止释放四个小球.相邻两小球释放的时间间隔为0.1s,某时刻拍下小球所处位置的照片,测出xAB=5cm,xBC=10cm,xCD=15 cm.则( )| A. | 小球从A点释放 | |
| B. | C点小球速度是A、D点小球速度之和的一半 | |
| C. | B点小球的速度大小为1.5 m/s | |
| D. | 所有小球的加速度大小为5 m/s2 |
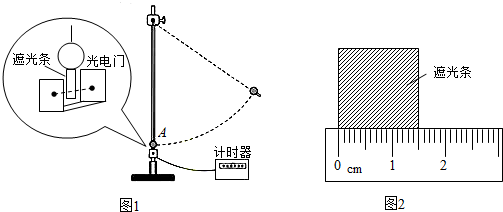
2.某同学用如图1所示的装置验证机械能守恒定律.一根细线系住钢球,悬挂着铁架台上,钢球静止于A点,光电门固定在A的正下方.在钢球底部竖直地粘住一片宽带为d的遮光条.将钢球拉至不同位置由静止释放,遮光条经过光电门的挡光时间t时由计时器测出,取v=$\frac{d}{t}$作为钢球经过A点时的速度.记录钢球每次下落的高度h和计时器示数t,计算并比较钢球在释放点和A点之间的势能变化大小△Ep与动能变化大小△Ek,就能验证机械能是否守恒.
(1)△Ep=mgh计算钢球重力势能变化的大小,式中钢球下落高度h应测量释放时的钢球球心到B之间的竖直距离.
(A)钢球在A点时的顶端
(B)钢球在A点时的球心
(C)钢球在A点时的底端
(2)用△Ek=$\frac{1}{2}$mv2计算钢球动能变化的大小,用刻度尺测量遮光条宽度,示数如图2所示,其读数为1.50cm.某次测量中,计时器的示数为0.0100s,则钢球的速度为v=1.50m/s.
(3)下表为该同学的实验结果:
他发现表中的△Ep与△Ek之间存在差异,认为这是由于空气阻力造成的.你是否同意他的观点?请说明理由.
(4)请你提出一条减小上述差异的改进建议.

(1)△Ep=mgh计算钢球重力势能变化的大小,式中钢球下落高度h应测量释放时的钢球球心到B之间的竖直距离.
(A)钢球在A点时的顶端
(B)钢球在A点时的球心
(C)钢球在A点时的底端
(2)用△Ek=$\frac{1}{2}$mv2计算钢球动能变化的大小,用刻度尺测量遮光条宽度,示数如图2所示,其读数为1.50cm.某次测量中,计时器的示数为0.0100s,则钢球的速度为v=1.50m/s.
(3)下表为该同学的实验结果:
| △Ep(×10-2J) | 4.892 | 9.786 | 14.69 | 19.59 | 29.38 |
| △Ek(×10-2J) | 5.04 | 10.1 | 15.1 | 20.0 | 29.8 |
(4)请你提出一条减小上述差异的改进建议.
9.甲、乙两列横波在同一介质中分别从波源M、N两点沿x轴相向传播,波速为2m/s,振幅相同;某时刻的图象如图所示.则( )


| A. | 甲乙两波的起振方向相反 | |
| B. | 甲乙两波的频率之比为3:2 | |
| C. | 再经过3s,平衡位置在x=7m出的质点振动方向向下 | |
| D. | 再经过3s,两波源间(不含波源)有5个质点位移为零 |
12.下列说法错误的是( )
| A. | 地球同步卫星相对于地面是静止的 | |
| B. | 地球同步卫星的角速度与地球自转的角速度相同 | |
| C. | 第一宇宙速度是7.9km/s | |
| D. | 正常绕地球作圆周运动的人造卫星的速度都大于7.9km/s |

