题目内容
9. 如图所示,倾角为θ的光滑斜面的长、宽分别为l和b,一物块从斜面左上方顶点P处水平射入,而从右下方顶点Q处离开斜面,试求:
如图所示,倾角为θ的光滑斜面的长、宽分别为l和b,一物块从斜面左上方顶点P处水平射入,而从右下方顶点Q处离开斜面,试求:(1)物块离开斜面时所用时间为多少?
(2)物块刚射入斜面时的速度为多少?
分析 (1)将物块的运动分解为沿斜面方向向下和沿斜面向右两个方向,在沿下面向下的方向上做初速度为0的匀加速直线运动,在沿斜面向右的方向上做匀速直线运动.根据沿斜面向下方向上位移,根据l=$\frac{1}{2}a{t}^{2}$,求出物块离开斜面时所用的时间.
(2)分运动与合运动具有等时性,根据v0=$\frac{b}{t}$求出物块刚射入斜面时的速度.
解答 解:(1)根据牛顿第二定律,物块沿斜面向下的加速度为:
a=$\frac{mgsinθ}{m}$=gsinθ.
由l=$\frac{1}{2}a{t}^{2}$,得:t=$\sqrt{\frac{2l}{gsinθ}}$.
故物块离开斜面所用的时间为$\sqrt{\frac{2l}{gsinθ}}$.
(2)物块刚射入斜面时的速度为:v0=$\frac{b}{t}$=b$\sqrt{\frac{gsinθ}{2l}}$
答:(1)物块离开斜面所用的时间 为$\sqrt{\frac{2l}{gsinθ}}$.
(2)物块刚射入斜面时的速度为 b$\sqrt{\frac{gsinθ}{2l}}$.
点评 解决本题的关键将该运动分解为沿斜面向下和沿斜面向右两个方向,在沿下面向下的方向上做初速度为0的匀加速直线运动,在沿斜面向右的方向上做匀速直线运动.

练习册系列答案
相关题目
14. 如图(a)所示,圆形线圈P静止在水平桌面上,其正上方悬挂一相同线圈Q,P和Q共轴,Q中通有变化电流,电流随时间变化的规律如图(b)所示,P所受的重力为G,桌面对P的支持力为FN,则( )
如图(a)所示,圆形线圈P静止在水平桌面上,其正上方悬挂一相同线圈Q,P和Q共轴,Q中通有变化电流,电流随时间变化的规律如图(b)所示,P所受的重力为G,桌面对P的支持力为FN,则( )
 如图(a)所示,圆形线圈P静止在水平桌面上,其正上方悬挂一相同线圈Q,P和Q共轴,Q中通有变化电流,电流随时间变化的规律如图(b)所示,P所受的重力为G,桌面对P的支持力为FN,则( )
如图(a)所示,圆形线圈P静止在水平桌面上,其正上方悬挂一相同线圈Q,P和Q共轴,Q中通有变化电流,电流随时间变化的规律如图(b)所示,P所受的重力为G,桌面对P的支持力为FN,则( )| A. | t1时刻FN>G | B. | t2时刻FN>G | C. | t3时刻FN=G | D. | t4时刻FN<G |
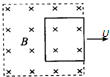
1.如图所示,先后以速度υ1和υ2匀速把一矩形线圈拉出有界匀强磁场区域,υ1=2υ2.在先后两种情况下( )

| A. | 线圈中的感应电流之比I1:I2=2:1 | |
| B. | 线圈中的感应电流之比I1:I2=1:2 | |
| C. | 线圈中产生的焦耳热之比Q1:Q2=4:1 | |
| D. | 通过线圈某截面的电荷量之比q1:q2=2:1 |
18. 如图,一小物块初速v1,开始由A点沿水平面滑至B点时速度为v2,若该物块仍以速度v1从A点沿两斜面滑动至B点时速度为v2′,已知斜面和水平面与物块的动摩擦因数相同,则( )
如图,一小物块初速v1,开始由A点沿水平面滑至B点时速度为v2,若该物块仍以速度v1从A点沿两斜面滑动至B点时速度为v2′,已知斜面和水平面与物块的动摩擦因数相同,则( )
 如图,一小物块初速v1,开始由A点沿水平面滑至B点时速度为v2,若该物块仍以速度v1从A点沿两斜面滑动至B点时速度为v2′,已知斜面和水平面与物块的动摩擦因数相同,则( )
如图,一小物块初速v1,开始由A点沿水平面滑至B点时速度为v2,若该物块仍以速度v1从A点沿两斜面滑动至B点时速度为v2′,已知斜面和水平面与物块的动摩擦因数相同,则( )| A. | v2>v2′ | B. | v2<v2′ | C. | v2=v2′ | D. | 无法比较 |
19. 如图所示是电子射线管示意图.接通电源后,电子射线由阴极沿x轴方向射出,在荧光屏上会看到一条亮线.要使荧光屏上的亮线向下(z轴负方向)偏转,在下列措施中可采用的是( )
如图所示是电子射线管示意图.接通电源后,电子射线由阴极沿x轴方向射出,在荧光屏上会看到一条亮线.要使荧光屏上的亮线向下(z轴负方向)偏转,在下列措施中可采用的是( )
 如图所示是电子射线管示意图.接通电源后,电子射线由阴极沿x轴方向射出,在荧光屏上会看到一条亮线.要使荧光屏上的亮线向下(z轴负方向)偏转,在下列措施中可采用的是( )
如图所示是电子射线管示意图.接通电源后,电子射线由阴极沿x轴方向射出,在荧光屏上会看到一条亮线.要使荧光屏上的亮线向下(z轴负方向)偏转,在下列措施中可采用的是( )| A. | 加一磁场,磁场方向沿z轴负方向 | B. | 加一磁场,磁场方向沿y轴正方向 | ||
| C. | 加一电场,电场方向沿z轴负方向 | D. | 加一电场,电场方向沿y轴正方向 |
 如图所示为某物体v-t图象,试说明该物体的运动情况.
如图所示为某物体v-t图象,试说明该物体的运动情况.