��Ŀ����
2��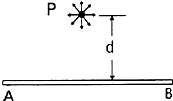 ��ͼ��ʾ�����㹻���ľ�Ե���Ϸ�����Ϊd��P����һ�����ӷ���Դ���ܹ���ֽ���������������������ȣ��Ⱥ�$\frac{q}{m}$=k�Ĵ���������ӣ����������Ӽ������ú�����������
��ͼ��ʾ�����㹻���ľ�Ե���Ϸ�����Ϊd��P����һ�����ӷ���Դ���ܹ���ֽ���������������������ȣ��Ⱥ�$\frac{q}{m}$=k�Ĵ���������ӣ����������Ӽ������ú�������������1������֪���ӵķ�������Ϊvo���ھ�Ե���Ϸ���һ�糡ǿ�ȴ�СΪE��������ֱ���µ���ǿ�糡����ͬһʱ�̷�����Ĵ������Ӵ��ϵ����ʱ��
��2�������ӵķ�������voδ֪���ھ�Ե����Ϸ�ֻ��һ����ֱֽ�棬�Ÿ�Ӧǿ���ʵ�����ǿ�ų���ʹ������Բ���˶����˶��뾶��Сǡ��Ϊd��Ϊʹͬʱ����������Ӵ��ϵ����ʱ����루1������ȣ���vo�Ĵ�С��
���� ��1��ͬһʱ�̷���������Ӵ��ϵ����ʱ���Ϊ��ֱ���Ϻ���ֱ������������ӣ�����˶�ѧ��ʽ������ʱ��
��2�����������ڴų����˶�ʱ�������������˶��켣����ϰ뾶��ʽ�����ڹ�ʽ��ͨ�����ι�ϵ�ó�vo�Ĵ�С��
��� �⣺��1����������ǿ�糡���˶��ļ��ٶȾ���ͬ�����ٶȣ�a=$\frac{qE}{m}$��
���ʱ���Ϊ��ֱ���Ϻ���ֱ������������ӣ������˶�ʱ��֮��Ϊ��t����t=$\frac{{2{v_0}}}{a}$��
���У�$\frac{q}{m}$=k����ã����ʱ���Ϊ $��t=\frac{{2{v_0}}}{kE}$��
��2�����ʱ���ӳ����ٶȵĴ�СΪv0��
�ڴų����˶�ʱ�������̵������˶��켣ʾ��ͼ���£�
�ɼ��ι�ϵ��֪���ʱ�䣺t1=$\frac{3}{4}T$�����ʱ�䣺t2=$\frac{1}{6}T$��
���������ڴų����˶�������$T=\frac{2��m}{qB}$��
�������⣺t1-t2=��t����ã�B=$\frac{7��E}{12{v}_{0}}$��
�����ڴų������ܵ����������ṩ��������
��ţ�ٵڶ����ɵã�qv0B=m$\frac{{v}_{0}^{2}}{R}$����ã�R=$\frac{m{v}_{0}}{qB}$��
�������֪��R=d����ã�v0=$\sqrt{\frac{7��kdE}{12}}$��
�𣺣�1��ͬһʱ�̷�����Ĵ������Ӵ��ϵ����ʱ���Ϊ$\frac{2{v}_{0}}{kE}$��
��2����vo�Ĵ�СΪ$\sqrt{\frac{7��kdE}{12}}$��
���� ���⿼���˴�����������ǿ�ų��е��˶���������������ǿ�ų���������Բ���˶������������ṩ��������ȷ���������ӹ켣�ķ�Χһ��Ӧ�û�ͼ�ķ����ҳ���ͬʱ���Խ�ϼ���֪ʶ���з�����

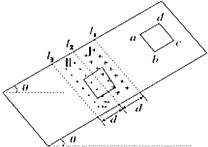 �����Ϊ�ȵĹ⻬б���ϣ�����Ϊd������ˮƽ����l1��l2��l3������֮��������ֱ���ڴ�ֱб�����ºʹ�ֱб�����ϵ���ǿ�ų����Ÿ�Ӧǿ�ȴ�С��ΪB��һ������Ϊm���߳�Ϊd���ܵ���ΪR�������ε��߿�l1�Ϸ�һ���ߴ��ɾ�ֹ��ʼ��б���»�����ab�߸�Խ��l1����ų���ʱ��ǡ�����ٶ�v1������ֱ���˶�����ab����Խ��l2�˶���l3֮ǰ��ij��ʱ�̣��߿��ֿ�ʼ���ٶ�v2������ֱ���˶����������ٶ�Ϊg�����߿���ͷŵ������ų��Ĺ����У�����˵����ȷ���ǣ�������
�����Ϊ�ȵĹ⻬б���ϣ�����Ϊd������ˮƽ����l1��l2��l3������֮��������ֱ���ڴ�ֱб�����ºʹ�ֱб�����ϵ���ǿ�ų����Ÿ�Ӧǿ�ȴ�С��ΪB��һ������Ϊm���߳�Ϊd���ܵ���ΪR�������ε��߿�l1�Ϸ�һ���ߴ��ɾ�ֹ��ʼ��б���»�����ab�߸�Խ��l1����ų���ʱ��ǡ�����ٶ�v1������ֱ���˶�����ab����Խ��l2�˶���l3֮ǰ��ij��ʱ�̣��߿��ֿ�ʼ���ٶ�v2������ֱ���˶����������ٶ�Ϊg�����߿���ͷŵ������ų��Ĺ����У�����˵����ȷ���ǣ�������| A�� | �߿��и�Ӧ�����ķ����ı� | |
| B�� | �߿�ab�ߴ�l1�˶���l2����ʱ����ڴ�l2�˶���l3����ʱ�� | |
| C�� | �߿����ٶ�v2����ֱ���˶�ʱ�����ȹ���Ϊ$\frac{{{m^2}{g^2}R}}{{4{B^2}{d^2}}}$sin2�� | |
| D�� | �߿��ab�߽���ų����ٶȱ�Ϊv2�Ĺ����У����ٵĻ�е�ܡ�E�����߿�����Ľ�����Q���Ĺ�ϵʽ�ǡ�E��=WG+$\frac{1}{2}$mv12-$\frac{1}{2}$mv22+Q�� |
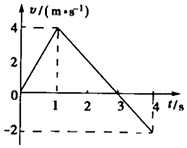 һ�ʵ���ֱ���˶���v-tͼ����ͼ��ʾ���Է����ʵ���˶����������
һ�ʵ���ֱ���˶���v-tͼ����ͼ��ʾ���Է����ʵ���˶����������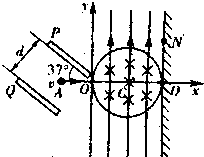 ��ͼ��ʾ��ƽ�а��������������P��Q��ˮƽ���37��ǣ����Ʋ�ΪU������ƽ��ֱ������ϵ������������P���¶�����������ԭ�㣬��D��0.2m��0������һ��ֱx���ӫ��������ӫ������y��֮������ֱ���ϵ���ǿ�糡���糡E=0.4N/C������C��0.1m��0����ΪԲ�ģ��뾶Ϊ0.1m��Բ���������д�ֱֽ���������ǿ�ų����Ÿ�Ӧǿ��$B=\frac{{2\sqrt{3}}}{15}T$��һ����m=4��10-7kg������q=1��10-5C�Ĵ������ӣ���A��$-\frac{1}{15}$m��0���㣨A��������ľ�����ȣ��ɾ�ֹ��ʼ��x����ֱ���˶���������ԭ��O����Բ�δų������������մ���ӫ������N�㣬g=10m/s2��sin37��=0.6����=3.14��$\sqrt{3}$=1.732
��ͼ��ʾ��ƽ�а��������������P��Q��ˮƽ���37��ǣ����Ʋ�ΪU������ƽ��ֱ������ϵ������������P���¶�����������ԭ�㣬��D��0.2m��0������һ��ֱx���ӫ��������ӫ������y��֮������ֱ���ϵ���ǿ�糡���糡E=0.4N/C������C��0.1m��0����ΪԲ�ģ��뾶Ϊ0.1m��Բ���������д�ֱֽ���������ǿ�ų����Ÿ�Ӧǿ��$B=\frac{{2\sqrt{3}}}{15}T$��һ����m=4��10-7kg������q=1��10-5C�Ĵ������ӣ���A��$-\frac{1}{15}$m��0���㣨A��������ľ�����ȣ��ɾ�ֹ��ʼ��x����ֱ���˶���������ԭ��O����Բ�δų������������մ���ӫ������N�㣬g=10m/s2��sin37��=0.6����=3.14��$\sqrt{3}$=1.732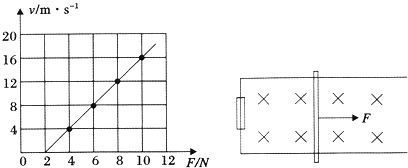
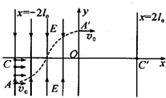 ��ͼ��ʾ��ֱ������ϵ�У���ֱ��x=-2l0��y�������ڴ�����������С��ȡ������෴���н���ǿ�糡������x���Ϸ��ĵ糡������y�Ḻ����x���·��ĵ糡������y���������ڵ糡��߽���A��-2l0��-l0����C��-2l0��0�������ڣ������ֲ��ŵ���Ϊ+q������Ϊm�����ӣ���ijʱ������A�㵽C�������ӣ�������������ͬ���ٶ�v0��x������������糡������A����������ӣ�ǡ�ô�y���ϵ�A�䣨0��l0����x������������糡����켣��ͼ��ʾ���������ӵ����������Ǽ������ã�
��ͼ��ʾ��ֱ������ϵ�У���ֱ��x=-2l0��y�������ڴ�����������С��ȡ������෴���н���ǿ�糡������x���Ϸ��ĵ糡������y�Ḻ����x���·��ĵ糡������y���������ڵ糡��߽���A��-2l0��-l0����C��-2l0��0�������ڣ������ֲ��ŵ���Ϊ+q������Ϊm�����ӣ���ijʱ������A�㵽C�������ӣ�������������ͬ���ٶ�v0��x������������糡������A����������ӣ�ǡ�ô�y���ϵ�A�䣨0��l0����x������������糡����켣��ͼ��ʾ���������ӵ����������Ǽ������ã�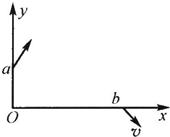 һ�����ʵ㣬����Ϊm�������Ϊq������y���300�ǵ��ٶ�v��y���ϵ�a�������ͼ�е�һ������������Ϊ��ʹ���ʵ��ܴ�x���b������x���600�ǵ��ٶ�����������ʵ��ĵط���һ����ֱ��xoyƽ�棬�Ÿ�Ӧǿ��ΪB����ǿ�ų������˴ų����ֲ���һ��Բ�������ڣ��������Բ�δų��������С�뾶���ʵ���������Բ��ƣ���
һ�����ʵ㣬����Ϊm�������Ϊq������y���300�ǵ��ٶ�v��y���ϵ�a�������ͼ�е�һ������������Ϊ��ʹ���ʵ��ܴ�x���b������x���600�ǵ��ٶ�����������ʵ��ĵط���һ����ֱ��xoyƽ�棬�Ÿ�Ӧǿ��ΪB����ǿ�ų������˴ų����ֲ���һ��Բ�������ڣ��������Բ�δų��������С�뾶���ʵ���������Բ��ƣ���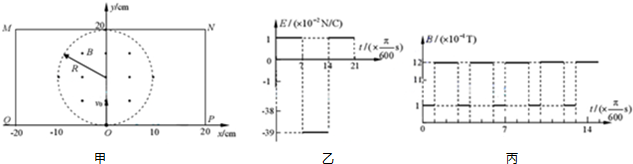
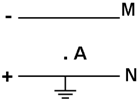 ��ͼ��ʾ����ƽ�н������缫��MN�糡�н������Ϊ-4��10-6C�ĵ��ɴ�A���Ƶ�M�壬�糡��������8��10-4 J���Ѹõ��ɴ�A���Ƶ�N�壬�糡��������Ϊ4��10-4J��N��ӵأ������Ϊ�����森��
��ͼ��ʾ����ƽ�н������缫��MN�糡�н������Ϊ-4��10-6C�ĵ��ɴ�A���Ƶ�M�壬�糡��������8��10-4 J���Ѹõ��ɴ�A���Ƶ�N�壬�糡��������Ϊ4��10-4J��N��ӵأ������Ϊ�����森��