题目内容
14.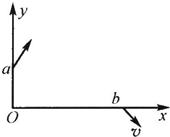 一带电质点,质量为m,电荷量为q,以与y轴成300角的速度v从y轴上的a点进入如图中第一象限所在区域,为了使该质点能从x轴的b点以与x轴成600角的速度射出,可在适当的地方加一个垂直于xoy平面,磁感应强度为B的匀强磁场,若此磁场仅分布在一个圆形区域内.试求这个圆形磁场区域的最小半径(质点的重力忽略不计).
一带电质点,质量为m,电荷量为q,以与y轴成300角的速度v从y轴上的a点进入如图中第一象限所在区域,为了使该质点能从x轴的b点以与x轴成600角的速度射出,可在适当的地方加一个垂直于xoy平面,磁感应强度为B的匀强磁场,若此磁场仅分布在一个圆形区域内.试求这个圆形磁场区域的最小半径(质点的重力忽略不计).
分析 由题意分析粒子的运动过程,明确粒子运动可能的轨迹;再根据牛顿第二定律求出半径;明确圆形磁场区域的最小面积是以磁场中圆周运动轨迹对应弦为直径的圆.
解答  解:根据牛顿第二定律:qv0B=m$\frac{v_0^2}{R}$,
解:根据牛顿第二定律:qv0B=m$\frac{v_0^2}{R}$,
则粒子在磁场中做圆周的半径为:R=$\frac{{m{v_0}}}{qB}$,
根据题意,粒子在磁场区域中的轨道为半径等于R的圆上的$\frac{1}{3}$圆周,这段圆弧应与入射方向的速度、出射方向的速度相切,如图所示,
则到入射方向所在直线和出射方向所在直线相距为R的O′点就是圆周的圆心.粒子在磁场区域中的轨道就是以O′为圆心、R为半径的圆上
的圆弧ef,而e点和f点应在所求圆形磁场区域的边界上,在通过e、f两点的不同的圆周中,最小的一个是以ef连线为直径的圆周.
即得圆形区域的最小半径为:r=Rsin60°=$\frac{{\sqrt{3}m{v_0}}}{2qB}$,
则这个圆形区域磁场的最小面积为:Smin=πr2=$\frac{3}{4}$π($\frac{{m{v_0}}}{qB}$)2
答:这个圆形区域磁场的最小面积为$\frac{3}{4}$π($\frac{{m{v_0}}}{qB}$)2.
点评 本题考查磁场区域面积的极值问题,此题的关键是确定出圆心,明确粒子可能的运动轨迹,且从a到b有圆周运动和一段直线运动.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
4.下列事例中有关速度的说法,正确的是( )
| A. | 汽车速度计上显示80 km/h,指的是平均速度 | |
| B. | 某高速公路上的限速为110 km/h,指的是平均速度 | |
| C. | 火车从济南到北京的速度约为220 km/h,指的是瞬时速度 | |
| D. | 子弹以900 km/h的速度从枪口射出,指的是瞬时速度 |
 如图所示,两块平行金属极板MN水平放置,板长L=1m.间距d=$\frac{\sqrt{3}}{3}$m,两金属板间电压UMN=1×104 V;在平行金属板右侧依次存在ABC和FGH两个全等的正三角形区域,正三角形ABC内存在垂直纸面向里的匀强磁场B1,三角形的上顶点A与上金属板M平齐,BC边与金属板平行,AB边的中点P恰好在下金属板N的右端点;正三角形FGH内存在垂直纸面向外的匀强磁场B2,已知A、F、G处于同一直线上.B、C、H也处于同一直线上.AF两点距离为$\frac{2}{3}$m.现从平行金属极板MN左端沿中心轴线方向入射一个重力不计的带电粒子,粒子质量m=3×10-10 kg,带电量q=+1×10-4 C,初速度v0=1×105 m/s.求:
如图所示,两块平行金属极板MN水平放置,板长L=1m.间距d=$\frac{\sqrt{3}}{3}$m,两金属板间电压UMN=1×104 V;在平行金属板右侧依次存在ABC和FGH两个全等的正三角形区域,正三角形ABC内存在垂直纸面向里的匀强磁场B1,三角形的上顶点A与上金属板M平齐,BC边与金属板平行,AB边的中点P恰好在下金属板N的右端点;正三角形FGH内存在垂直纸面向外的匀强磁场B2,已知A、F、G处于同一直线上.B、C、H也处于同一直线上.AF两点距离为$\frac{2}{3}$m.现从平行金属极板MN左端沿中心轴线方向入射一个重力不计的带电粒子,粒子质量m=3×10-10 kg,带电量q=+1×10-4 C,初速度v0=1×105 m/s.求: 如图所示,在真空中有一水平放置的不带电平行板电容器,板间距离为d,极板长为L,上板B接地,现有大量质量均为m,带电荷量为+q的小油滴,以相同的初速度持续不断地从两板正中间沿图中虚线所示方向射入,第一滴油滴正好落到下板A的正中央P点.如果能落到A板的油滴仅有N(N未知)滴,且第N+1滴油滴刚好能从下极板边缘飞离电场,假设落到A板的油滴的电荷量能被板全部吸收,不考虑油滴间的相互作用,重力加速度为g.求:
如图所示,在真空中有一水平放置的不带电平行板电容器,板间距离为d,极板长为L,上板B接地,现有大量质量均为m,带电荷量为+q的小油滴,以相同的初速度持续不断地从两板正中间沿图中虚线所示方向射入,第一滴油滴正好落到下板A的正中央P点.如果能落到A板的油滴仅有N(N未知)滴,且第N+1滴油滴刚好能从下极板边缘飞离电场,假设落到A板的油滴的电荷量能被板全部吸收,不考虑油滴间的相互作用,重力加速度为g.求: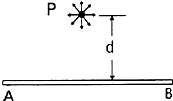 如图所示,在足够长的绝缘板上方距离为d的P点有一个粒子发射源,能够在纸面内向各个方向发射速率相等,比荷$\frac{q}{m}$=k的带正电的粒子,不考虑粒子间的相互作用和粒子重力.
如图所示,在足够长的绝缘板上方距离为d的P点有一个粒子发射源,能够在纸面内向各个方向发射速率相等,比荷$\frac{q}{m}$=k的带正电的粒子,不考虑粒子间的相互作用和粒子重力.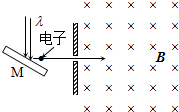 波长为λ的单色光照射某金属M表面产生光电效应,发射的光电子(电量绝对值为e,质量为m)经狭缝s后垂直进入磁感应强度为B的均匀磁场,如图所示.今已测出电子在该磁场中作圆运动的最大半径为R,求:
波长为λ的单色光照射某金属M表面产生光电效应,发射的光电子(电量绝对值为e,质量为m)经狭缝s后垂直进入磁感应强度为B的均匀磁场,如图所示.今已测出电子在该磁场中作圆运动的最大半径为R,求: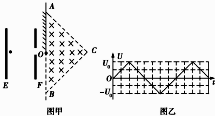 如图甲所示,在平行板电容器上加上如图乙所示的交变电压,在贴近E处有一粒子放射源,能够逐渐发射出大量质量为m,电荷量为q的带正电粒子,忽略粒子离开放射源时的初速度及粒子间的相互作用力,粒子只在电场力作用下运动,在电场中运动的时间极短可认为平行板间电压不变.从极板F射出的粒子能够继续沿直线向右运动,并由O点射入右侧的等腰直角三角形磁场区域.等腰直角三角形ABC的直角边边长为L.O为斜边AB的中点,在OA边上放有荧光屏,已知所有粒子刚好不能从AC边射出磁场,接收到粒子的荧光屏区域能够发光.求:
如图甲所示,在平行板电容器上加上如图乙所示的交变电压,在贴近E处有一粒子放射源,能够逐渐发射出大量质量为m,电荷量为q的带正电粒子,忽略粒子离开放射源时的初速度及粒子间的相互作用力,粒子只在电场力作用下运动,在电场中运动的时间极短可认为平行板间电压不变.从极板F射出的粒子能够继续沿直线向右运动,并由O点射入右侧的等腰直角三角形磁场区域.等腰直角三角形ABC的直角边边长为L.O为斜边AB的中点,在OA边上放有荧光屏,已知所有粒子刚好不能从AC边射出磁场,接收到粒子的荧光屏区域能够发光.求: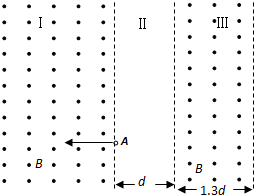 如图所示,一个带正电的粒子沿磁场边界从A点射入左侧磁场,粒子质量为m,电荷量为q,其中区域Ⅰ、Ⅲ内是垂直纸面向外的匀强磁场,左边区域足够大,右边区域宽度为1.3d,磁感应强度大小均为B,区域Ⅱ是两磁场间的无场区,两条竖直虚线是其边界线,宽度为d;粒子从左边界线A点射入磁场后,经过Ⅰ、Ⅱ、Ⅲ区域后能回到A点,若粒子在左侧磁场中的半径为d,整个装置在真空中,不计粒子的重力.
如图所示,一个带正电的粒子沿磁场边界从A点射入左侧磁场,粒子质量为m,电荷量为q,其中区域Ⅰ、Ⅲ内是垂直纸面向外的匀强磁场,左边区域足够大,右边区域宽度为1.3d,磁感应强度大小均为B,区域Ⅱ是两磁场间的无场区,两条竖直虚线是其边界线,宽度为d;粒子从左边界线A点射入磁场后,经过Ⅰ、Ⅱ、Ⅲ区域后能回到A点,若粒子在左侧磁场中的半径为d,整个装置在真空中,不计粒子的重力.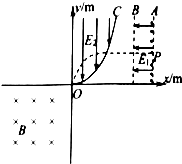 如图所示,平面直角坐标系xOy第一象限AB区域内分布沿x轴负向的匀速强电场,电场强度E1=1×104V/m,电场宽度d=0.01m,C为抛物线,y轴为其对称轴,原点为其顶点,在抛物线C和y轴之间存在沿y轴负向的匀强电场,电场强度E2=8×102V/m,在整个第三象限存在垂直纸面向里的匀速磁场,磁感应强度B=1×10-2T,在电场E1的右边界处有大量正离子,在电场的作用下由静止开始运动,离子的比荷$\frac{q}{m}$=5×107C/kg,发现位置P(5,2)处的离子经加速后进入电场E2偏转后恰好经过原点,不计离子间的相互作用和重力,求:
如图所示,平面直角坐标系xOy第一象限AB区域内分布沿x轴负向的匀速强电场,电场强度E1=1×104V/m,电场宽度d=0.01m,C为抛物线,y轴为其对称轴,原点为其顶点,在抛物线C和y轴之间存在沿y轴负向的匀强电场,电场强度E2=8×102V/m,在整个第三象限存在垂直纸面向里的匀速磁场,磁感应强度B=1×10-2T,在电场E1的右边界处有大量正离子,在电场的作用下由静止开始运动,离子的比荷$\frac{q}{m}$=5×107C/kg,发现位置P(5,2)处的离子经加速后进入电场E2偏转后恰好经过原点,不计离子间的相互作用和重力,求: