题目内容
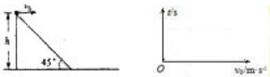
9. 如图所示,两块竖直放置的平行金属板A、B,板长为L,板间距离为d.在A、B两板的竖直对称轴上有一个带电小球(如图所示),质量为m,电量为q.若在两板间加上电压UAB=$\frac{mgd}{q}$,并加上垂直纸面向外的匀强磁场,磁感应强度B=$\frac{m\sqrt{gd}}{qd}$.将小球由静止释放,小球能刚好从A板下端飞出,且经过该处时刚好瞬时平衡.试问:
如图所示,两块竖直放置的平行金属板A、B,板长为L,板间距离为d.在A、B两板的竖直对称轴上有一个带电小球(如图所示),质量为m,电量为q.若在两板间加上电压UAB=$\frac{mgd}{q}$,并加上垂直纸面向外的匀强磁场,磁感应强度B=$\frac{m\sqrt{gd}}{qd}$.将小球由静止释放,小球能刚好从A板下端飞出,且经过该处时刚好瞬时平衡.试问:(1)小球带何种电性.
(2)小球以何方向从A板下端飞出?速度大小是多少?
(3)小球释放时距离A、B两板上端的连线有多高?
分析 (1)根据粒子的受力情况以及经过该处时的瞬时平衡关系可明确小球的电性;
(2)分析小球的受力情况,根据平衡关系可明确小球的运动方向和速度大小;
(3)对全程根据动能定理可求得小球释放时距离AB两板上端的连线高度.
解答  解:(1)由题意可知,粒子离开A下极板时处于平衡状态,则受力如图所示.
解:(1)由题意可知,粒子离开A下极板时处于平衡状态,则受力如图所示.
故小球一定带正电荷;
(2)由Eq=$\frac{{U}_{AB}}{d}q$=mg,知,要使粒子处于平衡状态,则电场力与重力的合力与洛伦兹力方向相反;
故速度方向是斜向左下方45°
由$Bqv=\sqrt{2}mg$,
得$v=\sqrt{2gd}$
(3)对全程用动能定理:$mg(h+L)-Eq•\frac{d}{2}=\frac{1}{2}m{v^2}$
解得:$h=\frac{3}{2}d-L$
答:(1)小球带正电.
(2)小球以与水平方向成45°角从A板下端飞出;速度大小是$\sqrt{2gd}$;
(3)小球释放时距离A、B两板上端的连线有$\frac{3}{2}d-L$
点评 本题考查带电粒子在复合场中的运动情况,要注意明确洛伦兹力、重力及电场力的性质,明确粒子在复合场中平衡条件的应用.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
5.一体重为600N的同学站在水平放置在升降机底板上的体重计上,当升降机在下降过程经历了加速、匀速和减速是三个阶段,则体重计的示数可能符合实际情况的一组是( )
| A. | 620N、600N、580N | B. | 580N、600N、620N | C. | 580N、620N、600N | D. | 620N、600N、600N |
17. 回旋加速器在科学研究中得到了广泛应用,其原理如图所示,D1和D2是两个中空的半圆形金属盒,置于与盒面垂直的匀强磁场中,它们接在电压为U、周期为T的交流电源上.位于D1圆心处的质子源A能不断产生质子(初速度可以忽略),它们在两盒之间被电场加速.当质子被加速到最大动能Ek后,再将它们引出.忽略质子在电场中的运动时间,则下列说法中( )
回旋加速器在科学研究中得到了广泛应用,其原理如图所示,D1和D2是两个中空的半圆形金属盒,置于与盒面垂直的匀强磁场中,它们接在电压为U、周期为T的交流电源上.位于D1圆心处的质子源A能不断产生质子(初速度可以忽略),它们在两盒之间被电场加速.当质子被加速到最大动能Ek后,再将它们引出.忽略质子在电场中的运动时间,则下列说法中( )
 回旋加速器在科学研究中得到了广泛应用,其原理如图所示,D1和D2是两个中空的半圆形金属盒,置于与盒面垂直的匀强磁场中,它们接在电压为U、周期为T的交流电源上.位于D1圆心处的质子源A能不断产生质子(初速度可以忽略),它们在两盒之间被电场加速.当质子被加速到最大动能Ek后,再将它们引出.忽略质子在电场中的运动时间,则下列说法中( )
回旋加速器在科学研究中得到了广泛应用,其原理如图所示,D1和D2是两个中空的半圆形金属盒,置于与盒面垂直的匀强磁场中,它们接在电压为U、周期为T的交流电源上.位于D1圆心处的质子源A能不断产生质子(初速度可以忽略),它们在两盒之间被电场加速.当质子被加速到最大动能Ek后,再将它们引出.忽略质子在电场中的运动时间,则下列说法中( )| A. | 若只增大交变电压U,则质子的最大动能Ek会变大 | |
| B. | 若只增大交变电压U,则质子在回旋加速器中运行时间缩短 | |
| C. | 质子第n次被加速前后的轨道半径之比为$\sqrt{n-1}$:$\sqrt{n}$ | |
| D. | 若只将交变电压的周期变为2T,仍可用此装置加速质子 |
1.关于平衡状态,下列说法正确的是( )
| A. | 当物体速度等于零时,物体处于平衡状态 | |
| B. | 运动的物体一定不是处于平衡状态 | |
| C. | 当物体处于平衡状态时,一定不受外力作用 | |
| D. | 若物体的运动状态保持不变,则物体处于平衡状态 |
18.如图所示,质量为m的物块始终静止在倾斜角为θ的斜面上,下列说法错误的是( )


| A. | 若斜面向右匀速移动距离s,斜面对物块没有做功 | |
| B. | 若斜面竖直向上匀速移动距离s,斜面对物块做功为零 | |
| C. | 若斜面向左以加速度a匀加速移动距离s,斜面对物块做功mas | |
| D. | 若斜面竖直向下以加速度a匀加速移动距离s,斜面对物块做功m(g+a)s |
 在“测定金属丝的电阻率”的实验中,需要测出金属丝的电阻Rx,甲乙两同学分别采用了不同的方法进行测量:
在“测定金属丝的电阻率”的实验中,需要测出金属丝的电阻Rx,甲乙两同学分别采用了不同的方法进行测量: