题目内容
18. 如图所示,粗糙的水平平台距地面高h=1.6m,平台右端有竖直向上的匀强电场,电场强度为E=5.0×103V/m.水平台左端挡板上固定一根轻质弹簧,弹簧的右端靠着一带电小滑块(与弹簧不固连),滑块质量为m=1.0kg,带电量为q=+1.0×10-3C.开始时弹簧被压缩,某时刻松开弹簧,小滑块运动到A点时与弹簧分离,并从水平台边缘的B点水平飞出,最后落在地面上的C点.已知小滑块与水平台间的动摩擦因数μ=0.25,s1=2.2m.落地点到平台的水平距离为s2=4.0m.运动过程中滑块带电量不变,不计空气阻力,g取10m/s2,求:
如图所示,粗糙的水平平台距地面高h=1.6m,平台右端有竖直向上的匀强电场,电场强度为E=5.0×103V/m.水平台左端挡板上固定一根轻质弹簧,弹簧的右端靠着一带电小滑块(与弹簧不固连),滑块质量为m=1.0kg,带电量为q=+1.0×10-3C.开始时弹簧被压缩,某时刻松开弹簧,小滑块运动到A点时与弹簧分离,并从水平台边缘的B点水平飞出,最后落在地面上的C点.已知小滑块与水平台间的动摩擦因数μ=0.25,s1=2.2m.落地点到平台的水平距离为s2=4.0m.运动过程中滑块带电量不变,不计空气阻力,g取10m/s2,求:(1)小滑块从平台边缘B点水平飞出时的速度的大小
(2)小滑块与弹簧分离时的速度大小.
分析 (1)根据高度求出平抛运动的时间,结合水平位移和时间求出平抛运动的初速度.
(2)根据牛顿第二定律求出匀减速运动的加速度,结合速度位移公式求出滑块与弹簧分离时的速度大小.
解答 解:(1)滑块从B运动到C,做类平抛运动,电场力:F=qE=1.0×10-3×5.0×103N=5N
物体在竖直方向的加速度:$a=\frac{mg-F}{m}=g-\frac{F}{m}=10-\frac{5}{1}=5m/{s}^{2}$
落地的时间为:${t}_{2}=\sqrt{\frac{2h}{a}}=\sqrt{\frac{2×1.6}{5}}=0.8$s,
则平抛运动的初速度为:${v}_{B}=\frac{{s}_{2}}{{t}_{2}}=\frac{4.0}{0.8}m/s=5.0$m/s.
(2)滑块从A到B做匀减速运动,加速度为:a′=$\frac{f}{m}=\frac{-μmg}{m}=-μg=-0.25×10m/{s}^{2}=-2.5m/{s}^{2}$,
根${v}_{B}^{2}-{v}_{A}^{2}=2a′{s}_{1}$.
代入数据解得:vA=6m/s
答:(1)滑块从平台边缘的B点水平飞出时的速度大小为5m/s;
(2)滑块与弹簧分离时的速度大小为6m/s.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,知道高度决定时间,初速度和时间共同决定水平位移.以及知道加速度是联系力学和运动学的桥梁.

练习册系列答案
相关题目
9.在空中相同高度处以相同速率分别抛出质量相同的三个小球,一个竖直向上抛,一个竖直向下抛,一个平抛,若不计空气的阻力,从三个小球抛出到落地的过程中( )
| A. | 三个小球动量的变化量相同 | |
| B. | 下抛小球和平抛小球动量变化量相同 | |
| C. | 上抛小球动量变化量最大 | |
| D. | 三个小球落地时的动能相同 |
6.设地球的半径为R,质量为m的卫星在距地面3R高处绕地球做匀速圆周运动,已知地面处的重力加速度为g,则( )
| A. | 卫星的线速度为$\sqrt{\frac{gR}{3}}$ | B. | 卫星的角速度为 $\sqrt{\frac{g}{64R}}$ | ||
| C. | 卫星的加速度为$\frac{g}{16}$ | D. | 卫星的周期为2π$\sqrt{\frac{64R}{g}}$ |
3.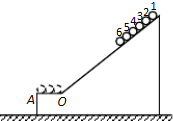 斜面体上开有凹槽,槽内紧挨放置六个半径均为r的相同刚性小球,各球编号如图,斜面与水平轨道OA平滑连接,OA长度为6r.现将六个小球由静止同时释放,小球离开A点后均做平抛运动,不计一切摩擦.则在各小球运动过程中,下列说法正确的是( )
斜面体上开有凹槽,槽内紧挨放置六个半径均为r的相同刚性小球,各球编号如图,斜面与水平轨道OA平滑连接,OA长度为6r.现将六个小球由静止同时释放,小球离开A点后均做平抛运动,不计一切摩擦.则在各小球运动过程中,下列说法正确的是( )
 斜面体上开有凹槽,槽内紧挨放置六个半径均为r的相同刚性小球,各球编号如图,斜面与水平轨道OA平滑连接,OA长度为6r.现将六个小球由静止同时释放,小球离开A点后均做平抛运动,不计一切摩擦.则在各小球运动过程中,下列说法正确的是( )
斜面体上开有凹槽,槽内紧挨放置六个半径均为r的相同刚性小球,各球编号如图,斜面与水平轨道OA平滑连接,OA长度为6r.现将六个小球由静止同时释放,小球离开A点后均做平抛运动,不计一切摩擦.则在各小球运动过程中,下列说法正确的是( )| A. | 球6的机械能守恒 | B. | 球6在OA段机械能增大 | ||
| C. | 球6的水平射程最大 | D. | 有三个球落地点位置相同 |


 如图所示,斜面长5cm、高1cm,工人用600N的力沿斜面把重2400N的箱子匀速推到车上,推力对箱子作的功是3000J,斜面的机械效率是60%.
如图所示,斜面长5cm、高1cm,工人用600N的力沿斜面把重2400N的箱子匀速推到车上,推力对箱子作的功是3000J,斜面的机械效率是60%. 如图所示,质点从A点开始沿半径r=20cm的圆周顺时针方向做匀速圆周运动,角速度为ω=$\frac{π}{3}$rad/s,则经过多长时间,质点的位移大小为20cm?
如图所示,质点从A点开始沿半径r=20cm的圆周顺时针方向做匀速圆周运动,角速度为ω=$\frac{π}{3}$rad/s,则经过多长时间,质点的位移大小为20cm?