题目内容
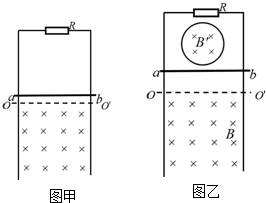
20. 如图所示,在方向垂直纸面向里,磁感应强度为B的匀强磁场区域中有一个由均匀导线制成的单匝矩形线框abcd,线框边长ab=2L,bc=L,线框导线的总电阻为R.将线框以恒定的速度v沿垂直磁场方向移出磁场,运动中线框始终在纸面所示的平面内运动.
如图所示,在方向垂直纸面向里,磁感应强度为B的匀强磁场区域中有一个由均匀导线制成的单匝矩形线框abcd,线框边长ab=2L,bc=L,线框导线的总电阻为R.将线框以恒定的速度v沿垂直磁场方向移出磁场,运动中线框始终在纸面所示的平面内运动.(1)若运动中线框cd边始终与磁场上边界垂直,则线框移出磁场的过程中,线框中产生的感应电流大小I=$\frac{BLv}{R}$或$\frac{2BLv}{R}$;流过线框ad边的电荷量q=$\frac{2B{L}_{\;}^{2}}{R}$.
(2)若运动中线框cd边始终与磁场右边界平行,则线框移出磁场的过程中,导体框ad边两端的电势差Uad=$\frac{BLv}{6}$或$-\frac{BLv}{3}$或$-\frac{5BLv}{6}$;线框中的电流在ad边产生的焦耳热Q=$\frac{{B}_{\;}^{2}{L}_{\;}^{3}v}{3R}$或$\frac{2{B}_{\;}^{2}{L}_{\;}^{3}v}{3R}$.
分析 根据感应电量q=$\frac{△Φ}{R}$,分析磁通量变化量关系,来求解感应电量;根据焦耳定律求解电流在ad边产生的热量.根据欧姆定律求得ad间的电压.
解答 解:(1)移出磁场过程中,①当线框短边切割磁感线产生的感应电动势为:
E=BLv
感应电流:$I=\frac{BLv}{R}$
②当线框长边切割磁感线产生的感应电动势E′=B•2L•v=2BLv
感应电流$I′=\frac{E′}{R}=\frac{2BLv}{R}$
无论怎么移出磁场,根据感应电量公式,得流过线框ad边的电荷量$q=\frac{△Φ}{R}=\frac{B•2{L}_{\;}^{2}}{R}=\frac{2B{L}_{\;}^{2}}{R}$
(2)设短边电阻为R,长边电阻为2R
①向上移出磁场,bc边切割磁感线,感应电动势E=BLv
根据楞次定律,感应电流顺时针,${U}_{ad}^{\;}=\frac{E}{R}×\frac{R}{6}=\frac{BLv}{6}$
线框中的电流在ad边产生的焦耳热$Q={I}_{\;}^{2}\frac{1}{6}R•t=(\frac{BLv}{R})_{\;}^{2}•\frac{1}{6}R•\frac{2L}{v}$=$\frac{{B}_{\;}^{2}{L}_{\;}^{3}v}{3R}$
②向上移出磁场,ad边切割磁感线,感应电动势E=BLv
根据楞次定律,感应电流a→d,电源的路端电压${U}_{ad}^{\;}=-\frac{BLv}{R}×\frac{5R}{6}=-\frac{5BLv}{6}$
线框中的电流在ad边产生的焦耳热$Q={I}_{\;}^{2}\frac{1}{6}R•t=(\frac{BLv}{R})_{\;}^{2}×\frac{1}{6}R×\frac{2L}{v}=\frac{{B}_{\;}^{2}{L}_{\;}^{3}v}{3R}$
③向左或右移出磁场,cd边切割磁感线,感应电动势E=2BLv
根据楞次定律,感应电流a→d,${U}_{ad}^{\;}=\\;-\frac{E}{R}×\frac{1}{6}R=-\frac{BLv}{6}$$-\frac{E}{R}×\frac{R}{6}=-\frac{2BLv}{6}=-\frac{1}{3}BLv$
线框中的电流在ad边产生的焦耳$Q={I}_{\;}^{2}×\frac{1}{6}Rt=(\frac{2BLv}{R})_{\;}^{2}×\frac{R}{6}×\frac{L}{v}$=$\frac{2{B}_{\;}^{2}{L}_{\;}^{3}v}{3R}$
故答案为:(1)电流大小为$\frac{BLv}{R}$或$\frac{2BLv}{R}$,流过线框截面的电量为$\frac{{2B{L^2}}}{R}$
(2)ad间的电压为$\frac{BLv}{6}$或$\frac{BLv}{3}$或-$\frac{5BLv}{6}$,
线框中的电流在ad边产生的热量为$\frac{{{B^2}{L^3}v}}{3R}$或$\frac{{2{B^2}{L^3}v}}{3R}$
点评 该题考查了法拉第电磁感应定律和闭合回路欧姆定律的应用,是一道常规题.要注意题目中线框边长不等,分清楚哪个边在切割磁感线.

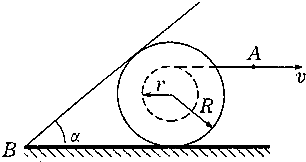
 有一体育娱乐比赛项目,其赛道俯视图如图所示,三根长度均为R的拦阻杆的一端固定在水平面上的O点,并能绕O点以角速度ω逆时针匀速转动,拦阻杆间的夹角为120°.AB为拦阻杆转动平面下方的一段水平传送带,传送带以速度v0匀速运动,方向如图所示,拦阻杆能够拦阻传送带的长度为$\sqrt{3}$R.若参赛者从A端踏上传送带,在传送带上不能与拦阻杆相遇,顺利到达B端即为赢得比赛.则参赛者相对传送带的最小运动速度为( )
有一体育娱乐比赛项目,其赛道俯视图如图所示,三根长度均为R的拦阻杆的一端固定在水平面上的O点,并能绕O点以角速度ω逆时针匀速转动,拦阻杆间的夹角为120°.AB为拦阻杆转动平面下方的一段水平传送带,传送带以速度v0匀速运动,方向如图所示,拦阻杆能够拦阻传送带的长度为$\sqrt{3}$R.若参赛者从A端踏上传送带,在传送带上不能与拦阻杆相遇,顺利到达B端即为赢得比赛.则参赛者相对传送带的最小运动速度为( )| A. | v=$\frac{3\sqrt{3}Rω+2π{v}_{0}}{2π}$ | B. | v=$\frac{3\sqrt{3}Rω+4π{v}_{0}}{4π}$ | C. | v=$\frac{3\sqrt{3}Rω-4π{v}_{0}}{4π}$ | D. | v=$\frac{3\sqrt{3}Rω}{4π}$ |
| A. | 电源两极间的电压等于电源电动势 | |
| B. | 电动势越大的电源,将其他形式的能转化为电能的本领越大 | |
| C. | 电源电动势的数值等于外电压之和 | |
| D. | 电源电动势与外电路的组成无关 |

| A. | 小物体与甲传送带之间的动摩擦因数比与乙之间的小 | |
| B. | 两传送带对小物体做功相等 | |
| C. | 物体在甲传送带上的重力做功的平均功率比在乙上的大 | |
| D. | 两传送带因与小物体摩擦产生的热量相等 |

| A. | 通过L1的电流为L2电流的2倍 | B. | 此时L1、L2和L3的电阻均为12Ω | ||
| C. | L1消耗的电功率为0.75 W | D. | L1消耗的电功率为L2电功率的4倍 |
| A. | 14m∕s | B. | 15m∕s | C. | 6m∕s | D. | 无法确定 |
 如图所示,固定放置的两光滑平行金属导轨,间距d=0.2m,在桌面上的部分是水平的,处在磁感应强度B=0.1T、方向竖直向下的有界磁场中.电阻R=3Ω.桌面高H=0.8m,金属杆ab质量m=0.2kg,电阻r=1Ω,在导轨上距桌面h=0.2m的高处由静止释放,运动过程中a、b两端始终与导轨接触良好并且高度相同.落地点距桌面左边缘的水平距离s=0.4m,g=10m/s2.求:
如图所示,固定放置的两光滑平行金属导轨,间距d=0.2m,在桌面上的部分是水平的,处在磁感应强度B=0.1T、方向竖直向下的有界磁场中.电阻R=3Ω.桌面高H=0.8m,金属杆ab质量m=0.2kg,电阻r=1Ω,在导轨上距桌面h=0.2m的高处由静止释放,运动过程中a、b两端始终与导轨接触良好并且高度相同.落地点距桌面左边缘的水平距离s=0.4m,g=10m/s2.求: