��Ŀ����
13�� ij��ʦ��ͼʾװ��̽���������������Ĺ�ϵ��A��B�ǿ���Ϊ���ɵ�������С���þ�Եϸ�߽�A���ң�ʵ�����ڸı�����ʱ���ƶ�B������A��B������ϸ�ߴ�ֱ����Q��q��ʾA��B�ĵ������d��ʾA��B��ľ��룬�ȣ��Ȳ��Ǻ�С����ʾϸ������ֱ����ļнǣ�x��ʾAƫ��O���ˮƽ���룮ʵ���У�������
ij��ʦ��ͼʾװ��̽���������������Ĺ�ϵ��A��B�ǿ���Ϊ���ɵ�������С���þ�Եϸ�߽�A���ң�ʵ�����ڸı�����ʱ���ƶ�B������A��B������ϸ�ߴ�ֱ����Q��q��ʾA��B�ĵ������d��ʾA��B��ľ��룬�ȣ��Ȳ��Ǻ�С����ʾϸ������ֱ����ļнǣ�x��ʾAƫ��O���ˮƽ���룮ʵ���У�������| A�� | dӦ���ֲ��� | B�� | B��λ����ͬһԲ���� | ||
| C�� | x�������˻�Qq������ | D�� | tan����A��B������������� |
���� ��С��AΪ�о����ı�������ƶ�B�Ĺ����У����ڶ�̬ƽ��״̬������A�������������G��������F1���ߵ�����F2���������ã�������ͼ�����ݼ��ι�ϵ���õ��ߵ�����F2���߳��Ĺ�ϵ���ٽ��з������
��� �⣺A�����⣬��װ��̽���������������Ĺ�ϵ������d���ֲ��䣻��A��ȷ�� B�����⣬��װ��̽���������������Ĺ�ϵ��d���䣬���ұ���A��B������ϸ�ߴ�ֱ��Aֻ������OΪԲ�ġ��뾶Ϊϸ�߳��ȵ�Բ�����˶�������B��λ����ͬһԲ���ϣ���B��ȷ��
B�����⣬��װ��̽���������������Ĺ�ϵ��d���䣬���ұ���A��B������ϸ�ߴ�ֱ��Aֻ������OΪԲ�ġ��뾶Ϊϸ�߳��ȵ�Բ�����˶�������B��λ����ͬһԲ���ϣ���B��ȷ��
C����С��AΪ�о��������ܵ�����G��������F1���ߵ�����F2���������ã���������ͼ��ͼ��
����F1��F2�ĺ���F������ƽ�������ã�F=G��
����AB������ʼ����ϸ�ߴ�ֱ������F1��F2ʼ�մ�ֱ�����ԣ�F1=mgsin�ȣ�F2=mgcos��
��ϸ�ߵij���ΪL����x=Lsin��
�ɿ��ض��ɣ�${F}_{1}=\frac{kQq}{{d}^{2}}$���ɵã�$\frac{kQq}{{d}^{2}}=mgsin��=mg•\frac{x}{L}$����x�������˻�Qq�����ȣ���C��ȷ��
D�������ϵķ���֪������F1=mgsin�ȣ�����sin����A��B������������ȣ���D����
��ѡ��ABC
���� ��������ѧ�ж�̬ƽ�����⣬���õ������������Ʒ����õ����Ĵ�С�������α߳��Ĺ�ϵ�����з�����Ҳ����Ӧ�ú�������⣮

 ��ͼ��ʾ����ƽ����ˮ������һ���ԴS�����Դ��ˮ��ľ���ΪH��ˮ�Ըù�Դ�����ĵ�ɫ���������Ϊn����ˮ���Ϸ����Կ���һԲ�ε����棬��Բ������İ뾶Ϊ��������
��ͼ��ʾ����ƽ����ˮ������һ���ԴS�����Դ��ˮ��ľ���ΪH��ˮ�Ըù�Դ�����ĵ�ɫ���������Ϊn����ˮ���Ϸ����Կ���һԲ�ε����棬��Բ������İ뾶Ϊ���������������õ������Ǻ�����ϵ��1+cot2��=$\frac{1}{{si{n^2}��}}$��tan��=$\frac{1}{cot��}$��
| A�� | $\frac{H}{{\sqrt{{n^2}-1}}}$ | B�� | $\frac{H}{{\sqrt{{n^2}+1}}}$ | C�� | H$\sqrt{{n^2}-1}$ | D�� | H$\sqrt{{n^2}+1}$ |
 ��ͼΪ�������������Ƶ����˶��Ĺ��ʾ��ͼ����ΪԲ�������Ϊ��Բ�����ABΪ��Բ�ij��ᣬ������͵��Ķ���ͬһƽ���ڣ�C��DΪ��������㣮��֪������ϵ������˶���C��ʱ�ٶȷ�����ABƽ�У�������˵����ȷ���ǣ�������
��ͼΪ�������������Ƶ����˶��Ĺ��ʾ��ͼ����ΪԲ�������Ϊ��Բ�����ABΪ��Բ�ij��ᣬ������͵��Ķ���ͬһƽ���ڣ�C��DΪ��������㣮��֪������ϵ������˶���C��ʱ�ٶȷ�����ABƽ�У�������˵����ȷ���ǣ�������| A�� | ��������ϵ������˶���C��ʱ�ļ��ٶȲ���ͬ | |
| B�� | ��������ϵ������˶���C��ʱ�����ļ��ٶȴ�С��� | |
| C�� | �������ڢ���������Ϊv1�������ڢ���B�������Ϊv2����v1��v2 | |
| D�� | �������ǵ��˶�������ͬ |
 ��ͼ��ʾ��MN��PQ�ǵ��費�Ƶ�ƽ�н������죬����ΪL�������������ֹ⻬��ƽֱ���ֲִڣ�����ƽ�����ӣ��Ҷ˽�һ����ֵΪR�Ķ�ֵ���裮ƽֱ���ֵ�����������п���Ϊd��������ֱ���ϡ��Ÿ�Ӧǿ�ȴ�СΪB����ǿ�ų�������Ϊm������ҲΪR�Ľ������Ӹ߶�Ϊh����ֹ�ͷţ�����ų��ұ߽紦ǡ��ֹͣ����֪��������ƽֱ���ֵ����Ķ�Ħ������Ϊ�̣��������뵼���Ӵ����ã�������������ų�����Ĺ����У�������
��ͼ��ʾ��MN��PQ�ǵ��費�Ƶ�ƽ�н������죬����ΪL�������������ֹ⻬��ƽֱ���ֲִڣ�����ƽ�����ӣ��Ҷ˽�һ����ֵΪR�Ķ�ֵ���裮ƽֱ���ֵ�����������п���Ϊd��������ֱ���ϡ��Ÿ�Ӧǿ�ȴ�СΪB����ǿ�ų�������Ϊm������ҲΪR�Ľ������Ӹ߶�Ϊh����ֹ�ͷţ�����ų��ұ߽紦ǡ��ֹͣ����֪��������ƽֱ���ֵ����Ķ�Ħ������Ϊ�̣��������뵼���Ӵ����ã�������������ų�����Ĺ����У�������| A�� | ������ֵ����ĵ���������N��Q | |
| B�� | ͨ���������ĵ����Ϊ$\frac{BdL}{2R}$ | |
| C�� | �������������Ӵ�ʱ���ٶȴ���$\sqrt{2gh}$ | |
| D�� | �����������Ľ�����Ϊ$\frac{1}{2}$��mgh-��mgd�� |
| A�� | �����ܵĵ�λ��ͬ�����ǵ���������Ҳ��ͬ | |
| B�� | �����Ĺ��̾�������������ת������ | |
| C�� | ���˶��ٹ������ж�������������ת�� | |
| D�� | ���ֲ�ͬ��ʽ���������Ի���ת����������ת�������У��ܵ��������غ�� |
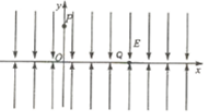 ��ͼ��ʾ����ֱƽ���ڵ�ֱ������ϵ�У���y��0�����ڣ�����y�Ḻ�������ǿ�糡����y��0�������ڣ�����y��������С��y��0������ȵ���ǿ�糡���Լ���ֱֽ�����ǿ�ų���ͼ��û�б������һ����Ϊm�������Ϊ+q������y����P�㣬����x��������СΪ2$\sqrt{gl}$�ij��ٶȿ�ʼ�˶���������һ�δ���x��ʱ��ǡ�õ���Q�㣻�����ڶ��δ���x��ʱ��ǡ�õ�������ԭ�㣻���������δ���x��ʱ��ǡ�õ���S�㣮��֪P��Q���㵽����ԭ��ľ���ֱ�Ϊl��2l���������ٶ�Ϊg����
��ͼ��ʾ����ֱƽ���ڵ�ֱ������ϵ�У���y��0�����ڣ�����y�Ḻ�������ǿ�糡����y��0�������ڣ�����y��������С��y��0������ȵ���ǿ�糡���Լ���ֱֽ�����ǿ�ų���ͼ��û�б������һ����Ϊm�������Ϊ+q������y����P�㣬����x��������СΪ2$\sqrt{gl}$�ij��ٶȿ�ʼ�˶���������һ�δ���x��ʱ��ǡ�õ���Q�㣻�����ڶ��δ���x��ʱ��ǡ�õ�������ԭ�㣻���������δ���x��ʱ��ǡ�õ���S�㣮��֪P��Q���㵽����ԭ��ľ���ֱ�Ϊl��2l���������ٶ�Ϊg���� ��ͼ��ʾ��ƽ������ϵOxy�У���y��0�����������y�Ḻ�������ǿ�糡����ǿ��СΪE����-h��y��0��������д��ڴ�ֱֽ���������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB����y��-h��������д��ڴ�ֱֽ���������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪ2B��A��y���ϵ�һ�㣬C��x���ϵ�һ�㣮һ����Ϊm�������Ϊq�Ĵ������������ijһ���ٶ���x���������A�����糡���̶�ͨ��C�����ٶȷ�����x��н�Ϊ��=30�����ų�������Դ�ֱ�߽�y=-h���ٶȽ���ų�����������������ƣ�����
��ͼ��ʾ��ƽ������ϵOxy�У���y��0�����������y�Ḻ�������ǿ�糡����ǿ��СΪE����-h��y��0��������д��ڴ�ֱֽ���������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB����y��-h��������д��ڴ�ֱֽ���������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪ2B��A��y���ϵ�һ�㣬C��x���ϵ�һ�㣮һ����Ϊm�������Ϊq�Ĵ������������ijһ���ٶ���x���������A�����糡���̶�ͨ��C�����ٶȷ�����x��н�Ϊ��=30�����ų�������Դ�ֱ�߽�y=-h���ٶȽ���ų�����������������ƣ�����
 ��ͼ��ʾ��L1��L2��L3Ϊ�����棬�����ڵ��������Ʋ���ͬ��ȡL2�ĵ���Ϊ�㣬��һ�������L1������Ϊ30J���˶���L3������Ϊ10J�����ɵĵ�����Ϊ15Jʱ�����Ķ����ǣ����������Ϳ�����������������
��ͼ��ʾ��L1��L2��L3Ϊ�����棬�����ڵ��������Ʋ���ͬ��ȡL2�ĵ���Ϊ�㣬��һ�������L1������Ϊ30J���˶���L3������Ϊ10J�����ɵĵ�����Ϊ15Jʱ�����Ķ����ǣ����������Ϳ�����������������