题目内容
4. 如图为两颗人造卫星绕地球运动的轨道示意图,Ⅰ为圆轨道,Ⅱ为椭圆轨道,AB为椭圆的长轴,两轨道和地心都在同一平面内,C、D为两轨道交点.己知轨道Ⅱ上的卫星运动到C点时速度方向与AB平行,则下列说法正确的是( )
如图为两颗人造卫星绕地球运动的轨道示意图,Ⅰ为圆轨道,Ⅱ为椭圆轨道,AB为椭圆的长轴,两轨道和地心都在同一平面内,C、D为两轨道交点.己知轨道Ⅱ上的卫星运动到C点时速度方向与AB平行,则下列说法正确的是( )| A. | 两个轨道上的卫星运动到C点时的加速度不相同 | |
| B. | 两个轨道上的卫星运动到C点时的向心加速度大小相等 | |
| C. | 若卫星在Ⅰ轨道的速率为v1,卫星在Ⅱ轨道B点的速率为v2,则v1<v2 | |
| D. | 两颗卫星的运动周期相同 |
分析 根据开普勒定律比较两卫星的运动周期,根据万有引力的大小,通过牛顿第二定律比较加速度,结合速度的大小比较向心加速度的大小.
解答 解:A、两个轨道上的卫星运动到C点时,所受的万有引力相等,根据牛顿第二定律知,加速度相同.故A错误;
B、因为两个轨道上的卫星在C点的万有引力加速度大小相等,而在轨道I上向心加速度与万有引力加速度大小相等,在轨道II上向心加速度等于于万有引力的切向分加速度,故可知在两个轨道上向心加速度大小是不等.故B错误;
C、B点为椭圆轨道的远地点,速度比较小,v1表示做匀速圆周运动的速度,v1>v2.故C错误;
D、根据几何关系知,椭圆的半长轴与圆轨道的半径相同,根据开普勒第三定律知,两颗卫星的运动周期相等.故D正确.
故选:D.
点评 本题考查万有引力定律、开普勒第三定律、牛顿第二定律等知识,知道卫星变轨的原理是解决本题的关键

练习册系列答案
相关题目
7. 如图所示,一辆小车静止在光滑水平面上,A、B两人分别站在车的两端.当两人同时相向运动时,下列选项正确的是 ( )
如图所示,一辆小车静止在光滑水平面上,A、B两人分别站在车的两端.当两人同时相向运动时,下列选项正确的是 ( )
 如图所示,一辆小车静止在光滑水平面上,A、B两人分别站在车的两端.当两人同时相向运动时,下列选项正确的是 ( )
如图所示,一辆小车静止在光滑水平面上,A、B两人分别站在车的两端.当两人同时相向运动时,下列选项正确的是 ( )| A. | 若小车不动,两人速率一定相等 | |
| B. | 若小车向左运动,A的动量一定比B的小 | |
| C. | 若小车向左运动,A的动量一定比B的大 | |
| D. | 若小车向左运动,A的速率一定比B的大 |
19. 在不少旅游景点里都设置了一种速降的游乐项目,从山上高处向山下低处安装一根钢索,人坐在吊篮里通过绳索和滑轮保持相对静止一起沿着倾角为θ的钢索快速下滑,如图所示,绳索与竖直方向间的夹角α,则下列说法正确的是( )
在不少旅游景点里都设置了一种速降的游乐项目,从山上高处向山下低处安装一根钢索,人坐在吊篮里通过绳索和滑轮保持相对静止一起沿着倾角为θ的钢索快速下滑,如图所示,绳索与竖直方向间的夹角α,则下列说法正确的是( )
 在不少旅游景点里都设置了一种速降的游乐项目,从山上高处向山下低处安装一根钢索,人坐在吊篮里通过绳索和滑轮保持相对静止一起沿着倾角为θ的钢索快速下滑,如图所示,绳索与竖直方向间的夹角α,则下列说法正确的是( )
在不少旅游景点里都设置了一种速降的游乐项目,从山上高处向山下低处安装一根钢索,人坐在吊篮里通过绳索和滑轮保持相对静止一起沿着倾角为θ的钢索快速下滑,如图所示,绳索与竖直方向间的夹角α,则下列说法正确的是( )| A. | 若α>θ,则人和吊篮至少受3个力的作用 | |
| B. | 若α>θ,则整个装置的加速度一定大于gsinθ | |
| C. | 若α=θ,则整个装置的加速度一定为gsinθ | |
| D. | 因为整个装置的加速度不可能大于gsinθ,所以α>θ不可能的 |
16.光纤可作为光传导工具,其传输原理是光的全反射.按照纤芯折射率分布情况可以分为突变型光纤和渐变型光纤,突变型光纤的纤芯的折射率是均匀的,而渐变型光纤的纤芯的折射率不均匀.下列关于这两种光纤说法正确的是( )
| A. | 突变型光纤的从光纤中心芯到玻璃包层的折射率是突然变大 | |
| B. | 渐变型光纤的从光纤中心芯到玻璃包层的折射率是逐渐变小 | |
| C. | 光在渐变型光纤中的传播轨迹是直折线 | |
| D. | 光在突变型光纤中的传播轨迹是曲线 |
13. 某老师用图示装置探究库仑力与电荷量的关系.A、B是可视为点电荷的两带电小球,用绝缘细线将A悬挂,实验中在改变电荷量时,移动B并保持A、B连线与细线垂直.用Q和q表示A、B的电荷量,d表示A、B间的距离,θ(θ不是很小)表示细线与竖直方向的夹角,x表示A偏离O点的水平距离.实验中( )
某老师用图示装置探究库仑力与电荷量的关系.A、B是可视为点电荷的两带电小球,用绝缘细线将A悬挂,实验中在改变电荷量时,移动B并保持A、B连线与细线垂直.用Q和q表示A、B的电荷量,d表示A、B间的距离,θ(θ不是很小)表示细线与竖直方向的夹角,x表示A偏离O点的水平距离.实验中( )
 某老师用图示装置探究库仑力与电荷量的关系.A、B是可视为点电荷的两带电小球,用绝缘细线将A悬挂,实验中在改变电荷量时,移动B并保持A、B连线与细线垂直.用Q和q表示A、B的电荷量,d表示A、B间的距离,θ(θ不是很小)表示细线与竖直方向的夹角,x表示A偏离O点的水平距离.实验中( )
某老师用图示装置探究库仑力与电荷量的关系.A、B是可视为点电荷的两带电小球,用绝缘细线将A悬挂,实验中在改变电荷量时,移动B并保持A、B连线与细线垂直.用Q和q表示A、B的电荷量,d表示A、B间的距离,θ(θ不是很小)表示细线与竖直方向的夹角,x表示A偏离O点的水平距离.实验中( )| A. | d应保持不变 | B. | B的位置在同一圆弧上 | ||
| C. | x与电荷量乘积Qq成正比 | D. | tanθ与A、B间库仑力成正比 |
14.物理学的发展极大地丰富了人类对物质世界的认识,推动了科学技术的创新和革命,促进了人类文明的进步,关于物理学中运动与力的发展过程和研究方法的认识,下列说法中正确的是( )
| A. | 笛卡尔首先提出了惯性的概念 | |
| B. | 牛顿三条运动定律是研究动力学问题的基石,牛顿的三条运动定律都能通过现代的实验手段直接验证 | |
| C. | 伽利略对自由落体运动研究方法的核心是:把实验和逻辑推理(包括数学演算)结合起来,从而发展了人类的科学思维方式和科学研究方法 | |
| D. | 力的单位“N“是基本单位,加速度的单位“m/s2”是导出单位 |
 如图所示,光滑的$\frac{1}{4}$圆弧轨道的半径为R=0.8m,一质量为m=1.0kg的物块自A点从静止开始下滑到圆弧轨道末端B点,然后沿水平面向右运动,到C点时速度刚好为零,B、C间的距离x=5m.重力加速度g取10m/s2.求:
如图所示,光滑的$\frac{1}{4}$圆弧轨道的半径为R=0.8m,一质量为m=1.0kg的物块自A点从静止开始下滑到圆弧轨道末端B点,然后沿水平面向右运动,到C点时速度刚好为零,B、C间的距离x=5m.重力加速度g取10m/s2.求:
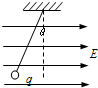 如图所示,一质量为m、带电量为q的小球,用绝缘细线悬挂在水平向右的匀强电场中,静止时悬线向左与竖直方向成θ角,重力加速度为g.判断小球带负电荷(正或负),电场强度E=$\frac{mgtanθ}{q}$.
如图所示,一质量为m、带电量为q的小球,用绝缘细线悬挂在水平向右的匀强电场中,静止时悬线向左与竖直方向成θ角,重力加速度为g.判断小球带负电荷(正或负),电场强度E=$\frac{mgtanθ}{q}$.