题目内容
1.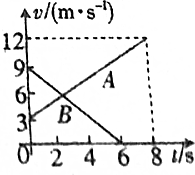 两个完全相同的物块A、B,在同一粗糙水平面上以不同的初速度从同一位置开始运动.图中两条直线分别表示物块受到水平拉力作用和不受拉力作用的v-t图象,求:
两个完全相同的物块A、B,在同一粗糙水平面上以不同的初速度从同一位置开始运动.图中两条直线分别表示物块受到水平拉力作用和不受拉力作用的v-t图象,求:(1)从开始到两物块第一次间距最远的时间.
(2)8s末物块A、B之间的距离x.
分析 (1)由速度时间图象得到物体的运动规律,然后根据速度时间公式求出加速度,当速度相等时,两物块第一次间距最远,进而求出时间;
(2)根据图象与坐标轴围成的面积表示位移分别求出物体AB的位移,从而得到两个物体的间距.
解答 解:(1)设A、B两物块的加速度大小分别为a1、a2,根据速度时间公式,有:
${a}_{1}=\frac{△{v}_{1}}{△{t}_{1}}=\frac{12-3}{8}=\frac{9}{8}m/{s}^{2}$…①
${a}_{2}=\frac{△{v}_{2}}{△{t}_{2}}=\frac{9}{6}=1.5m/{s}^{2}$…②
设经过时间t,AB速度相等,则有:
vB0-a2t=vA0+a1t
解得:t=$\frac{16}{7}s$
当速度相等时,两物块第一次间距最远,即经过时间$\frac{16}{7}s$,两物块第一次间距最远.
(2)设A、B两物块8s内的位移分别为x1、x2,图象得:
${x}_{1}=\frac{1}{2}×(3+12)×8=60m$,
${x}_{2}=\frac{1}{2}×9×6=27m$
所以有:x=x1-x2=60-27=33m
即8s末物块A、B之间的距离x为33m.
答:(1)从开始到两物块第一次间距最远的时间为$\frac{16}{7}s$.
(2)8s末物块A、B之间的距离x为33m.
点评 本题关键是根据速度时间图象得到两物体的运动情况,知道图象的斜率表示加速度,图象与坐标轴围成的面积表示位移.

练习册系列答案
相关题目
9. 矩形滑块由不同材料的上、下两层粘合在一起组成,将其放在光滑的水平面上,如图所示,质量为m的子弹以速度v水平射向滑块,若射击上层,则子弹刚好不穿出,若射击下层,子弹刚好嵌入,则上述两种情况相比较( )
矩形滑块由不同材料的上、下两层粘合在一起组成,将其放在光滑的水平面上,如图所示,质量为m的子弹以速度v水平射向滑块,若射击上层,则子弹刚好不穿出,若射击下层,子弹刚好嵌入,则上述两种情况相比较( )
 矩形滑块由不同材料的上、下两层粘合在一起组成,将其放在光滑的水平面上,如图所示,质量为m的子弹以速度v水平射向滑块,若射击上层,则子弹刚好不穿出,若射击下层,子弹刚好嵌入,则上述两种情况相比较( )
矩形滑块由不同材料的上、下两层粘合在一起组成,将其放在光滑的水平面上,如图所示,质量为m的子弹以速度v水平射向滑块,若射击上层,则子弹刚好不穿出,若射击下层,子弹刚好嵌入,则上述两种情况相比较( )| A. | 两次子弹对滑块做的功一样多 | |
| B. | 子弹嵌入上层过程中比嵌入下层过程中产生的热量多 | |
| C. | 子弹嵌入上层过程中,子弹减少的动能大于木块增加的动能 | |
| D. | 子弹击嵌入下层过程中,子弹动量的变化量等于木块动量的变化量 |
16. 把质量是0.1kg的小球放在竖立的轻质弹簧上,并把球往下按至A的位置,如图甲所示.迅速松手后,弹簧把球弹起,球升至最高位置C(图丙),途中经过位置B时弹簧正好处于自由状态(图乙).已知B、A的高度差为0.1m,C、B的高度差为0.2m,忽略空气阻力,重力加速度g=10m/s2.可知( )
把质量是0.1kg的小球放在竖立的轻质弹簧上,并把球往下按至A的位置,如图甲所示.迅速松手后,弹簧把球弹起,球升至最高位置C(图丙),途中经过位置B时弹簧正好处于自由状态(图乙).已知B、A的高度差为0.1m,C、B的高度差为0.2m,忽略空气阻力,重力加速度g=10m/s2.可知( )
 把质量是0.1kg的小球放在竖立的轻质弹簧上,并把球往下按至A的位置,如图甲所示.迅速松手后,弹簧把球弹起,球升至最高位置C(图丙),途中经过位置B时弹簧正好处于自由状态(图乙).已知B、A的高度差为0.1m,C、B的高度差为0.2m,忽略空气阻力,重力加速度g=10m/s2.可知( )
把质量是0.1kg的小球放在竖立的轻质弹簧上,并把球往下按至A的位置,如图甲所示.迅速松手后,弹簧把球弹起,球升至最高位置C(图丙),途中经过位置B时弹簧正好处于自由状态(图乙).已知B、A的高度差为0.1m,C、B的高度差为0.2m,忽略空气阻力,重力加速度g=10m/s2.可知( )| A. | 状态乙中小球的动能是0.1J | |
| B. | 状态甲中弹簧的弹性势能是0.3J | |
| C. | 由状态乙至状态丙,动能全部转化为重力势能 | |
| D. | 由状态甲至状态乙,弹性势能全部转化为动能 |
18.以下说法正确的是( )
| A. | 洗衣机脱水时,衣服上的水因受离心力作用而做离心运动 | |
| B. | 做圆周运动的物体,加速度一定指向圆心 | |
| C. | 做曲线运动的物体,速度可能是均匀变化的 | |
| D. | 只要物体所受合力发生变化,物体就会做曲线运动 |
19.两个互相垂直的恒力F1和F2作用在同一物体上,使物体发生一段位移后,物体克服力F1做功为6J,力F2对物体做功为8J,则力F1与F2的合力对物体做功为( )
| A. | 2 J | B. | 7 J | C. | 14 J | D. | 10 J |
 光滑水平面上放着一质量为M的槽,槽与水平面相切且光滑,如图所示,一质量为m的小球以v0向槽运动,若开始时槽固定不动,求小球上升的高度(槽足够高);若槽不固定,则小球上升的高度又为多少?
光滑水平面上放着一质量为M的槽,槽与水平面相切且光滑,如图所示,一质量为m的小球以v0向槽运动,若开始时槽固定不动,求小球上升的高度(槽足够高);若槽不固定,则小球上升的高度又为多少?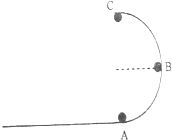 如图所示,竖直的半圆形轨道与水平面相切,轨道半径R=0.2m,质量m=200g的小球以某一速度正对半圆形轨道运动,A、B、C三点分别为圆轨道最低点,与圆心等高点、最高点.小球过这三点的速度分别为:v1=5m/s,v2=4m/s,v3=3m/s,求:
如图所示,竖直的半圆形轨道与水平面相切,轨道半径R=0.2m,质量m=200g的小球以某一速度正对半圆形轨道运动,A、B、C三点分别为圆轨道最低点,与圆心等高点、最高点.小球过这三点的速度分别为:v1=5m/s,v2=4m/s,v3=3m/s,求: